Skip to main content
SpringerLink
Log in

A new insight into onset of inertial flow in porous media using network modeling with converging/diverging pores

  • Original Paper
  • Published:
Computational Geosciences Aims and scope Submit manuscript

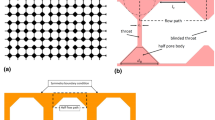
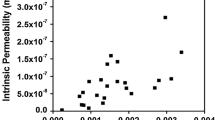
Abstract

The network modeling approach is applied to provide a new insight into the onset of non-Darcy flow through porous media. The analytical solutions of one-dimensional Navier-Stokes equation in sinusoidal and conical converging/diverging throats are used to calculate the pressure drop/flow rate responses in the capillaries of the network. The analysis of flow in a single pore revealed that there are two different regions for the flow coefficient ratio as a function of the aspect ratio. It is found that the critical Reynolds number strongly depends on the pore geometrical properties including throat length, average aspect ratio, and average coordination number of the porous media, and an estimation of such properties is required to achieve more reliable predictions. New criteria for the onset of non-Darcy flow are also proposed to overcome the lack of geometrical data. Although the average aspect ratio is the main parameter which controls the inertia effects, the effect of tortuosity on the onset of non-Darcy flow increases when the coordination number of media decreases. In addition, the higher non-Darcy coefficient does not essentially accelerate the onset of inertial flow. The results of this work can help to better understand how the onset of inertial flow may be controlled/changed by the pore architecture of porous media.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Forchheimer: Hydrolik. Teubner, Leipzing and Berlin (1914)

    Google Scholar 

  2. Ergun, S.: Fluid flow through packed column. Chem. Eng. Prog. 48(2), 89–94 (1952)

    Google Scholar 

  3. Huang, H., Ayoub, J.A.: Applicability of the Forchheimer equation for non-Darcy flow in porous media. SPE J. 13(01), 112–122 (2008)

    Article  Google Scholar 

  4. Chaudhary, K., Cardenas, M.B., Deng, W., Bennett, P.C.: The role of eddies inside pores in the transition from Darcy to Forchheimer flowsGeophysical Research Letters 38(24) (2011)

  5. Ruth, D., Ma, H.: On the derivation of the Forchheimer equation by means of the average theorem. Transp. Porous Medias 7(3), 225–264 (1992)

    Google Scholar 

  6. Whitaker, S.: The Forchheimer equation: a theoretical development. Transp. Porous Media 25, 27–61 (1996)

    Article  Google Scholar 

  7. Barr, D.w.: Turbulent flow through porous media. Ground Water 39(5), 646–650 (2000)

    Article  Google Scholar 

  8. Forchheimer: Wasserbewegung durch Boden. Z. Ver. Dtsch. Ing. 45(5), 1781–1788 (1901)

    Google Scholar 

  9. Fand, R., Kim, B., Lam, A., Phan, R.: Resistance to the flow of fluids through simple and complex porous media whose matrices are composed of randomly packed spheres. J. Fluids Eng. 109(3), 268–274 (1987)

    Article  Google Scholar 

  10. Chaudhary, K., Cardenas, M.B., Deng, W., Bennett, P.C.: Pore geometry effects on intrapore viscous to inertial flows and on effective hydraulic parameters. Water Resour. Res. 49(2), 1149–1162 (2013)

    Article  Google Scholar 

  11. Mei, C., Auriault, J.-L.: The effect of weak inertia on flow through a porous medium. J. Fluid Mech. 222, 647–663 (1991)

    Article  Google Scholar 

  12. Fourar, M., Radilla, G., Lenormand, R., Moyne, C.: On the non-linear behavior of a laminar single-phase flow through two and three-dimensional porous media. Adv. Water Resour. 27(6), 669–677 (2004)

    Article  Google Scholar 

  13. Balhoff, M., Mixkelić, A., Wheeler, M.F.: Polynomial filtration laws for low Reynolds number flows through porous media. Transp. Porous Medias 81(1), 35–60 (2010)

    Article  Google Scholar 

  14. Dullien, F.A.: Porous media: fluid transport and pore structure. Academic (2012)

  15. Chen, Z., Lyons, S.L., Qin, G.: Derivation of the Forchheimer law via homogenization. Transp. Porous Medias 44(2), 325–335 (2001)

    Article  Google Scholar 

  16. Hassanizadeh, S.M., Gray, W.G.: High velocity flow in porous media. Transp. Porous Medias 2, 521–531 (1987)

    Google Scholar 

  17. Balhoff, M.T., Wheeler, M.F.: A predictive pore-scale model for non-Darcy flow in porous media. SPE J. 14, 579–587 (2009)

    Article  Google Scholar 

  18. Ewing, R.E., Lazarov, R.D., Lyons, S.L., Papavassiliou, D.V., Papavassiliou, J., Qin, G.: Numerical well model for non-Darcy flow through isotropic porous media. Computat. Geosci. 3, 185–204 (1999)

    Article  Google Scholar 

  19. Chilton, T.H., Colburn, A.P.: Pressure drop in packed tubes. Ind Engngc. Chem. 23(8), 913–919 (1931)

    Article  Google Scholar 

  20. Tek, M.R.: Development of a generalized Darcy equation. Trans. AIME 210, 376–377 (1957)

    Google Scholar 

  21. Wright, D.E.: Non-linear flow through granular media. J. Hyd. Div. Trans. ASCE 94, 851 (1968)

    Google Scholar 

  22. deVries, J.: Prediction of non-Darcy flow in porous media. J. lrrig. Drain. Div. ASCE IR2 (1979)

  23. Green, L.J., Duwez, P.: Fluid flow through porous metals. J. Appl. Mech 18, 39–45 (1951)

    Google Scholar 

  24. Leonormand, R., Touboul, E., Zarcone, C.: Numerical models and experiments on immiscible displacements in porous media. J. Fluid Mech. 189, 165–187 (1988)

    Article  Google Scholar 

  25. Dillard, L.A., Blunt, M.J.: Development of a pore network simulation model to study nonaqueous phase liquid dissolution. Water Resour. Res. 36(2), 439–454 (2000)

    Article  Google Scholar 

  26. Lopez, X., Valvatne, P.H., Blunt, M.J.: Predictive network modeling of single-phase non-Newtonian flow in porous media. J. Colloid. Interf. Sci. 264(1), 256–265 (2003)

    Article  Google Scholar 

  27. Balhoff, M.T., Thompson, K.E.: Modeling the steady flow of yield-stress fluids in packed beds. AIChE J. 50(12), 3034–3048 (2004)

    Article  Google Scholar 

  28. Chaouche, M., Rakotomalala, N., Salin, D., Xu, B., Yorstos, Y.C.: Capillary effects in drainage in heterogeneous porous media. Chem. Engng. Sci. 49, 2447–2466 (1994)

    Article  Google Scholar 

  29. Sahimi, M.: Flow phenomena in rocks: from continuum models to fractals, percolation, cellular automata, and simulated annealing. Rev. Mod. Phys. 65, 1393–1534 (1993)

    Article  Google Scholar 

  30. Thauvin, F., Mohanty, K.K.: Network modeling of non-Darcy flow through porous media. Transp. Porous Media 19, 19–37 (1998)

    Article  Google Scholar 

  31. Wang, X., Thauvin, F., Mohanty, K.K.: Non-Darcy flow through anisotropic porous media. Chem. Eng. Sci. 54, 1859–1869 (1999)

    Article  Google Scholar 

  32. Piri, M., Blunt, M.J.: Three-dimensional mixed-wet random pore-scale network modeling of two- and three-phase flow in porous media. I. Model description. Phys. Rev. E: Stat. Phys., Plasmas, Fluids 71, 026301 (2005)

    Article  Google Scholar 

  33. Stark, K.P.: Fundamentals of transport phenomena in porous media, vol. 2. Elsevier, Amsterdam (1972)

    Google Scholar 

  34. Du Plessis, J.P., Masliyah, J.H.: Mathematical modeling of flow through consolidated isotropic porous media. Transp. Porous Media 3, 145–161 (1988)

    Article  Google Scholar 

  35. Ma, H., Ruth, D.W.: The microscopic analysis of high Forchheimer number flow in porous media. Transp. Porous Media 13, 139–160 (1993)

    Article  Google Scholar 

  36. Zeng, Z., Grigg, R.: A criterion for non-Darcy flow in porous media. Transp. Porous Media 63, 57–69 (2006)

    Article  Google Scholar 

  37. Martins, A.A., Laranjeira, P.E., Lopes, J.C.B., Dias, M.M.: Network modeling of flow in a packed bed. AIChE J. 53(1), 91–107 (2007)

    Article  Google Scholar 

  38. Fatt, M.: The network model of porous media. I. Capillary pressure characteristics. Pet. Trans. 207, 142–164 (1956)

    Google Scholar 

  39. Thompson, K.E., Fogler, H.S.: Modelling flow in disordered packed beds from pore-scale fluid mechanics. AIChE J. 43, 1377–1389 (1997)

    Article  Google Scholar 

  40. Krohn, C.E., Thompson, A.H.: Fractal sandstones pores: automated measurements using scanning-electron microscope images. Phys. Rev. B Condens. Matter. 33, 6366–6374 (1986)

    Article  Google Scholar 

  41. Caruso, L., Simmons, G., Wilkens, R.: The physical properties of a set of sandstone—part 1. The samples. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 22, 381–392 (1985)

    Article  Google Scholar 

  42. Lao, H.-W., Neeman, H.J., Papavassilou, D.V.: A pore network model for the calculation of non-Darcy flow coefficients in fluid flow through porous media. Chem. Eng. Comm. 191(10), 1285–1322 (2004)

    Article  Google Scholar 

  43. Mohanty, K.K., Salter, S.J.: Multiphase flow in porous media: II. pore-level modeling. Paper presented at the Annual Fall Technical Conference of the SPE-AIME, New Orleans

  44. Veyskarami, M., Hassani, A.H., Mohammad Hossein Ghazanfari, M.H.: Modeling of non-Darcy flow through anisotropic porous media: role of pore space profiles. Chem. Eng. Sci. 151, 93–104 (2016)

    Article  Google Scholar 

  45. Arns, J.-Y., Robins, V., Sheppard, A.P., Sok, R.M., Pinczewski, W.V., Knackstedt, M.A.: Effect of network topology on relative permeability. Transp. Porous Media 55(1), 21–46 (2004)

    Article  Google Scholar 

  46. Raoof, A., Hassanizadeh, S.M.: A new method for generating pore-network models of porous media. Transp. Porous Media 81(3), 391–407 (2010)

    Article  Google Scholar 

  47. Ioannidis, M., Chatzis, I.: On the geometry and topology of 3D stochastic porous media. J. Colloid Interface Sci. 229(2), 323–334 (2000)

    Article  Google Scholar 

  48. Sok, R.M., Knackstedt, M.A., Sheppard, A.P., Pinczewski, W.V., Lindquist, W., Venkatarangan, A., Paterson, L.: Direct and stochastic generation of network models from tomographic images; effect of topology on residual saturations. Transp. Porous Media 46(2-3), 345–371 (2002)

    Article  Google Scholar 

  49. Vasilyev, L., Raoof, A., Nordbotten, J.M.: Effect of mean network coordination number on dispersivity characteristics. Transport Porous Media (2012)

  50. Ioannidis, M., Chatzis, I.: Network modelling of pore structure and transport properties of porous media. Chem. Eng. Sci. 54, 1859–1869 (1993)

    Google Scholar 

  51. Diaz, C.E., Chatzis, I., Dullien, F.A.L.: Simulation of capillary pressure curves using bond correlated site percolation on a simple cubic network. Transp. Porous Med 2, 215–240 (1987)

    Article  Google Scholar 

  52. Sochi, T.: Newtonian flow in converging-diverging capillaries. arXiv:1108.0163v2 (2012)

  53. Formaggia, L., Lamponi, D., Quarteroni, A.: One-dimensional models for blood flow in arteries. J. Eng. Math. 47(3/4), 251–276 (2003)

    Article  Google Scholar 

  54. Sochi, T.: Newtonian flow in converging-diverging capillaries. Int. J. Model. Simul. Sci. Comput. 4(03), 1350011 (2013)

    Article  Google Scholar 

  55. Cengel, Y., Cimbala, J.: Fluid mechanics; fundamentals and application. McGraw-Hill, New York (2006)

    Google Scholar 

  56. Jones, S.: Using the inertial coefficient, b, to characterize heterogeneity in reservoir rock. Society of Petroleum Engineers, SPE Annual Technical Conference and Exhibition (1987)

  57. Janicek, J.D., Katz, D.L.V.: Applications of unsteady state gas flow calculations (1955)

  58. Coles, M., Hartman, K.: Non-Darcy measurements in dry core and the effect of immobile liquid. In: SPE Gas Technology Symposium. Society of Petroleum Engineers (1998)

  59. Geertsma, J.: Estimating the coefficient of inertial resistance in fluid flow through porous media. Soc. Pet. Eng. J. 14(05), 445–450 (1974)

    Article  Google Scholar 

  60. Firoozabadi, A., Katz, D.L.: An analysis of high-velocity gas flow through porous media. J. Pet. Technol. 31(02), 211–216 (1979)

    Article  Google Scholar 

  61. Kataja, M., Rybin, A., Timonen, J.: Permeability of highly compressible porous medium. J. Appl. Phys. 72, 1271 (1992)

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the Salehi’s graphical group and Amir Hossein Mousavi for their help in providing the graphical figures.

Author information

Authors and Affiliations

  1. Chemical and Petroleum Engineering Department, Sharif University of Technology, Azadi Ave, Tehran, Iran

    Maziar Veyskarami, Amir Hossein Hassani & Mohammad Hossein Ghazanfari

Authors
  1. Maziar Veyskarami
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amir Hossein Hassani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohammad Hossein Ghazanfari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maziar Veyskarami.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Veyskarami, M., Hassani, A.H. & Ghazanfari, M.H. A new insight into onset of inertial flow in porous media using network modeling with converging/diverging pores. Comput Geosci 22, 329–346 (2018). https://doi.org/10.1007/s10596-017-9695-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10596-017-9695-3

Keywords

Search

Navigation