Abstract
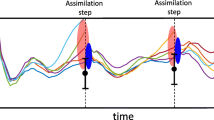
The ensemble Kalman filter has been successfully applied for data assimilation in very large models, including those in reservoir simulation and weather. Two problems become critical in a standard implementation of the ensemble Kalman filter, however, when the ensemble size is small. The first is that the ensemble approximation to cross-covariances of model and state variables to data can indicate the presence of correlations that are not real. These spurious correlations give rise to model or state variable updates in regions that should not be updated. The second problem is that the number of degrees of freedom in the ensemble is only as large as the size of the ensemble, so the assimilation of large amounts of precise, independent data is impossible. Localization of the Kalman gain is almost universal in the weather community, but applications of localization for the ensemble Kalman filter in porous media flow have been somewhat rare. It has been shown, however, that localization of updates to regions of non-zero sensitivity or regions of non-zero cross-covariance improves the performance of the EnKF when the ensemble size is small. Localization is necessary for assimilation of large amounts of independent data. The problem is to define appropriate localization functions for different types of data and different types of variables. We show that the knowledge of sensitivity alone is not sufficient for determination of the region of localization. The region depends also on the prior covariance for model variables and on the past history of data assimilation. Although the goal is to choose localization functions that are large enough to include the true region of non-zero cross-covariance, for EnKF applications, the choice of localization function needs to balance the harm done by spurious covariance resulting from small ensembles and the harm done by excluding real correlations. In this paper, we focus on the distance-based localization and provide insights for choosing suitable localization functions for data assimilation in multiphase flow problems. In practice, we conclude that it is reasonable to choose localization functions based on well patterns, that localization function should be larger than regions of non-zero sensitivity and should extend beyond a single well pattern.
Similar content being viewed by others
References
Agbalaka, C.C., Oliver, D.S.: Application of the EnKF and localization to automatic history matching of facies distribution and production data. Math. Geosci. 40(4), 353–374 (2008)
Anderson, J.L.: Exploring the need for localization in ensemble data assimilation using a hierarchical ensemble filter. Physica, D: Nonlinear Phenom. 230(1–2), 99–111 (2007)
Anterion, F., Karcher, B., Eymard, R.: Use of parameter gradients for reservoir history matching, SPE-18433. In: Proc. of the SPE Symposium on Reservoir Simulation, 6–8 February 1989, Houston, pp. 339–354 (1989)
Arroyo-Negrete, E., Devegowda, D., Datta-Gupta, A., Choe, J.: Streamline-assisted ensemble Kalman filter for rapid and continuous reservoir model updating. SPE Reserv. Evalu. Eng. 11(6), 1046–1060 (2008)
Burgers, G., van Leeuwen, P.J., Evensen, G.: Analysis scheme in the ensemble Kalman filter. Mon. Weather Rev. 126, 1719–1724 (1998)
Carter, R.D., Kemp, L.F., Pierce, A.C.: Discussion of comparison of sensitivity coefficient calculation methods in automatic history matching. SPE J. 22(4), 205–208 (1982)
Chen, Y., Oliver, D.S.: Ensemble-based closed-loop optimization applied to Brugge Field (SPE 118926). SPE Reserv. Evalu. Eng. (2009, in press)
Devegowda, D., Arroyo-Negrete, E., Datta-Gupta, A., Douma, S.G.: Efficient and robust reservoir model updating using ensemble Kalman filter with sensitivity-based covariance localization (SPE-106144). In: SPE Reservoir Simulation Symposium (2007)
Dong, Y., Gu, Y., Oliver, D.S.: Sequential assimilation of 4D seismic data for reservoir description using the ensemble Kalman filter. J. Pet. Sci. Eng. 53(1–2), 83–99 (2006)
Fertig, E.J., Hunt, B.R., Ott, E., Szunyogh, I.: Assimilating non-local observations with a local ensemble Kalman filter. Tellus A 59(5), 719–730 (2007)
Furrer, R., Bengtsson, T.: Estimation of high-dimensional prior and posterior covariance matrices in Kalman filter variants. J. Multivar. Anal. 98(2), 227–255 (2007)
Gaspari, G., Cohn, S.E.: Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 125(554), 723–757 (1999)
Hacker, J.P., Anderson, J.L., Pagowski, M.: Improved vertical covariance estimates for ensemble-filter assimilation of near-surface observations. Mon. Weather Rev. 135(3), 1021–1036 (2007)
Hamill, T.M., Whitaker, J.S., Snyder, C.: Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter. Mon. Weather Rev. 129(11), 2776–2790 (2001)
Houtekamer, P.L., Mitchell, H.L.: Data assimilation using an ensemble Kalman filter technique. Mon. Weather Rev. 126(3), 796–811 (1998)
Houtekamer, P.L., Mitchell, H.L.: A sequential ensemble Kalman filter for atmospheric data assimilation. Mon. Weather Rev. 129(1), 123–137 (2001)
Houtekamer, P.L., Mitchell, H.L., Pellerin, G., Buehner, M., Charron, M., Spacek, L., Hansen, B.: Atmospheric data assimilation with an ensemble Kalman filter: results with real observations. Mon. Weather Rev. 133(3), 604–620 (2005)
Jacquard, P.: Théorie de l’interprétation des mesures de pression. Rev. Ins. Fr. Pét. 19(3), 297–334 (1964)
Li, R., Reynolds, A.C., Oliver, D.S.: Sensitivity coefficients for three-phase flow history matching. J. Can. Pet. Technol. 42(4), 70–77 (2003)
Lorenc, A.C.: The potential of the ensemble Kalman filter for NWP—a comparison with 4D-Var. Q. J. R. Meteorol. Soc. 129(595), 3183–3203 (2003)
Oliver, D.S., Reynolds, A.C., Liu, N.: Inverse Theory for Petroleum Reservoir Characterization and History Matching, first edn. Cambridge University Press, Cambridge (2008)
Skjervheim, J.-A., Evensen, G., Aanonsen, S.I., Ruud, B.O., Johansen, T.A.: Incorporating 4D seismic data in reservoir simulation models using ensemble Kalman filter. SPE J. 12(3), 282–292 (2007)
Vasco, D.W., Yoon, S., Datta-Gupta, A.: Integrating dynamic data into high-resolution reservoir models using streamline-based analytic sensitivity coefficients. SPE J. 4(4), 389–399 (1999)
Wu, Z., Reynolds, A.C., Oliver, D.S.: Conditioning geostatistical models to two-phase production data. SPE J. 4(2), 142–155 (1999)
Zhang, Y., Oliver, D.S.: History matching using a hierarchical stochastic model with the ensemble Kalman filter: a field case study, SPE-118879. In: Proceedings of the 2009 SPE Reservoir Simulation Symposium, The Woodlands, 2–4 February 2009
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chen, Y., Oliver, D.S. Cross-covariances and localization for EnKF in multiphase flow data assimilation. Comput Geosci 14, 579–601 (2010). https://doi.org/10.1007/s10596-009-9174-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10596-009-9174-6