Abstract
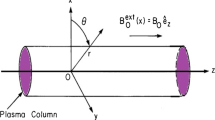
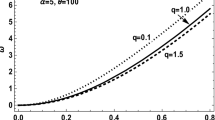
In order to further study on radiation of a moving electron in poloidal magnetized plasma (PMP), theoretical analysis and simulation calculation of Cherenkov radiation (CR) under the condition of an accelerated electron beam in PMP are respectively presented in this paper. Through analysis of dielectric tensor in poloidal magnetized plasma with uniformly accelerated electron and description of beam-wave interaction in PMP by Maxwell’s equations, radiation mechanism of uniformly accelerated electron CR in PMP is described. Then eigenvalue and radiation condition are respectively obtained. Moreover, dispersion relation of radiation wave is also deduced through analysis of eigenvalues. At the same time, through analysis of effect that cyclotron frequency and plasma frequency have on eigenvalue, it is discovered that plasma frequency has great effect on not only p1 mode but also p2 mode, but cyclotron frequency only affects p2 mode. Finally, through simulation calculation, dispersion curves of both p1 mode and p2 mode are presented. Through comparing to the case of uniform moving electrons, the radiation conditions of the accelerated electrons are more relaxed, more prone to generate radiation. The theoretical analysis and simulation calculation can provide for further research of the radiation microwave in PMP.









Similar content being viewed by others
References
Liu, S.G., Zhang, P., Liu, W.H., et al.: Surface polariton Cherenkov light radiation source. Phys. Rev. Lett. 109(15), 153902 (2012)
Yasumoto, K., Shigematsu, H.: Analysis of propagation characteristics of radio waves in tunnels using a surface impedance approximation. Radio Sci. 19(2), 597–602 (1984)
Shchagin, A.V.: Fresnel coefficients for parametric X-ray (Cherenkov) radiation. Phys. Usp. 58(8), 819–827 (2015)
Harms, J., Rose, P.B., Erickson, A.: Characterization of gamma-ray cross talk in Cherenkov-based detectors for active interrogation imaging applications. IEEE Sens. J. 17(20), 6707–6715 (2017)
Liu, S.G., Zhang, Y.X., Yan, Y., et al.: Cherenkov radiation by an electron bunch moving in Hermitian medium. J. Appl. Phys. 102(4), 044901 (2007)
Dobrynina, A.A., Mikheev, N.V., Raffelt, G.G.: Radiative decay of keV-mass sterile neutrinos in a strongly magnetized plasma. Phys. Rev. D 90(11), 113015 (2014)
Li, L.M., Cheng, G.X., Zhang, L., et al.: Role of the rise rate of beam current in the microwave radiation of vircator. J. Appl. Phys. 109(7), 074504 (2011)
Kartashov, I.N., Kuzelev, M.V.: Cherenkov instability of a magnetized beam-plasma system with allowance for a momentum spread of beam electrons. Phys. Wave Phenom. 25(1), 43–51 (2017)
Chen, C.M., Bai, Y.L., Zhang, J., et al.: Numerical study of oblique incidence of terahertz wave to magnetized plasma. High Power Laser Part. Beams 30(1), 51–55 (2018)
Hematizadeh, A., Jazayeri, S.M.: Study of terahertz radiation generation by two laser beams in an axial magnetized rippled density plasma. IEEE Trans. Plasma Sci. 45(7), 1717–1722 (2017)
Shao, T., Liu, F., Hai, B., et al.: Surface modification of epoxy using an atmospheric pressure DBD to accelerate surface charge dissipation. IEEE Trans. Dielectr. Electr. Insul. 24(3), 1557–1565 (2017)
Tian, W., Chen, S.X., Xiao, J.X., et al.: Dispersion of Cherenkov radiation by electron uniform moving in poloidal magnetized plasma. Sens. Transducers 158(11), 274–278 (2013)
Gai, F., Chen, S.X., Chen, K., Li, J., et al.: Conduction characteristics of long-gap triggered vacuum switch. High Power Laser Part. Beams 24(4), 847–850 (2012)
Zhang, W.X., Zhao, X.P., Zhao, S.T., et al.: Study on partial discharge detection of 10 kV power cable. Telkomnika 10(7), 1795–1799 (2012)
Tian, W., Gai, F., Chen, S.X., et al.: Experiment study on influence of trigger current on conduction characteristics of triggered vacuum switches. Trans. China Electrotech. Soc. 32(20), 28–33 (2017)
Li, X., Zhou, Z.S., Chen, P.Y., et al.: Study and application of the multi-gap for gas discharge. Trans. China Electrotech. Soc. 32(20), 70–76 (2017)
Wang, R.X., Hai, B., Tian, S.L., et al.: Optimization of dielectric material surface charge measurement and impact of plasma treatment on their surface electrical characteristics. High Volt. Eng. 43(6), 1808–1815 (2017)
Tian, W., Chen, S.X., Gai, F., et al.: Analysis of Cherenkov angle by electron uniform moving in poloidal magnetized plasma. Sens. Transducers 32(5), 3637–3646 (2014)
Acknowledgements
The authors acknowledge the National Natural Science Foundation of China (Grants 51641708 and 51207171) and 2018 Hubei Provincial Natural Science Foundation of China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Tian, W., Zhang, J., Wang, L. et al. Dispersion analysis and calculation on Cherenkov radiation of an accelerated electron beam in poloidal magnetized plasma. Cluster Comput 22 (Suppl 4), 8879–8886 (2019). https://doi.org/10.1007/s10586-018-2007-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10586-018-2007-4