Abstract
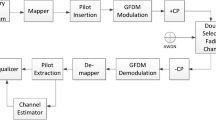
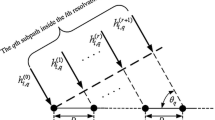
Cyclic delay diversity (CDD), employing multiple antennas provides increased frequency-selectivity and thereby achieves frequency diversity using forward error correction in orthogonal frequency division multiplexing (OFDM). However, channel estimation of CDD OFDM becomes crucial over frequency-selective fading channels. In this paper, we propose a low-complexity channel estimation technique for CDD OFDM systems over time-varying channels using basis expansion model. We first analyze the frequency correlation of CDD OFDM channels and then design scattered pilot structure for estimating the channel coefficients. In the proposed channel estimator, Slepian sequences are employed estimate the channel impulse response by exploiting the frequency correlation of CDD OFDM over time-varying channel. Simulation results demonstrated that the proposed channel estimator achieves better mean square error and bit-error-rate performance compared with that of existing methods over time-varying channels.





Similar content being viewed by others
References
Cui, T., Tellambura, C., Wu, Y.: Low-complexity pilot-aided channel estimation for OFDM systems over doubly-selective channels. In: IEEE International Conference on Communications, 2005. ICC 2005, vol. 3, pp. 1980–1984 (2005)
Chen, Y.F., Sheen, W.-H., Wang, L.-C.: Optimization of cyclic-delay diversity aided frequency-selective scheduling in OFDMA downlink systems. IEEE Trans. Veh. Technol. 63(4), 1645–1659 (2014)
Zhang, Y., Cosmas, J., Bard, M., Song, Y.H.: Diversity gain for DVB-H by using transmitter receiver cyclic delay diversity. IEEE Trans. Broadcast 52(4), 464–474 (2006)
Rahman, M., Witrisal, K., Das, S., Fitzek, F.H.P., Olsen, O., Prasad, R.: Optimum pre-DFT combining with cyclic delay diversity for OFDM based WLAN systems. In: 2004 IEEE 59th Vehicular Technology Conference, 2004. VTC 2004-Spring, vol. 4, pp. 1844–1848 (2004)
Lee, D., Jung, Y.S., Lee, J.H.: Cooperative coding using cyclic delay diversity for OFDM systems. ICICE Trans. Commun. 9, 2354–2362 (2010)
Kim, Y.J., Kim, H.Y., Li, D.W.: On the optimal cyclic delay value in cyclic delay diversity. IEEE Trans. Broadcast. 55(4), 790–795 (2009)
Bauch, G., Malik, J.S.: Cyclic delay diversity with bit-interleaved coded modulation in orthogonal frequency division multiple access. IEEE Trans. Wirel. Commun. 5(8), 2092–2100 (2006)
Auer, G.: Channel estimation for OFDM with cyclic delay diversity. In: 15th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, 2004. PIMRC 2004, vol. 3, pp. 1792–1796 (2004)
Auer, G.: Channel estimation by set partitioning for OFDM with cyclic delay diversity. In: Proc. IEEE Veh. Tech. Conf. (2004)
Hou, W., Wang, X.: Excessively long channel estimation for CDD OFDM systems using superimposed pilots. In: 2011 IEEE International Conference on Communications (ICC), pp. 1–5 (2011)
Lu, S., Al-Dhahir, N.: A novel CDD-OFDM scheme with pilot-aided channel estimation. IEEE Trans. Wirel. Commun. 8(3), 1122–1127 (2009)
Rossi, P.S., Mller, R.R., Edfors, O.: Linear MMSE estimation of time-frequency variant channels for MIMO-OFDM systems. Signal Process. 91(5), 1157–1167 (2011)
Chiong, C., Rong, Y., Xiang, Y.: Channel estimation for time-varying MIMO relay systems. IEEE Trans. Wirel. Commun. 14, 6752–6762 (2015)
Song, F.Y.L., Lei, X., Jin, M.: Optimal complex exponentials BEM and channel estimation in doubly selective channel. Chaos Solitons Fractal 89, 465–473 (2016)
Song, F.Y.L., Lei, X., Jin, M.: Spatial-temporal bem and channel estimation strategy for massive mimo time-varying systems. IEEE Global Communications Conference (GLOBECOM) 2016, 1–6 (2016)
Tang, G.L.Z., Cannizzaro, R.C., Banelli, P.: Pilot-assisted time-varying channel estimation for OFDM systems. IEEE Trans. Signal Process 55(5), 2226–2238 (2007)
Zemen, T., Mecklenbrauker, C.: Time-variant channel estimation using discrete prolate spheroidal sequences. IEEE Trans. Signal Process 53(9), 3597–3607 (2005)
Van De Ville, D., Philips, W., Lemahieu, I.: On the N-dimensional extension of the discrete prolate spheroidal window. IEEE Signal Process. Lett. 9, 89–91 (2002)
Rossi, P.S., Muller, R.: Slepian-based two-dimensional estimation of time-frequency variant MIMO-OFDM channels. IEEE Signal Process. Lett. 15, 21–24 (2008)
Rappaport, T.: Wireless Communication: Principles and Practice. Prentice Hall, New Jersey (2002)
Tang, S., Gong, K., Song, J., Pan, C., Yang, Z.: Intercarrier interference cancellation with frequency diversity for OFDM systems. IEEE Trans. Broadcast. 53, 132–137 (2007)
Wei, L., Kennedy, R., Lamahewa, T.A.: An optimal basis of band-limited functions for signal analysis and design. IEEE Signal Process. Lett. 58(11), 5744–5755 (2010)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Raja, A., Thulasibai, V. & Senthil, B. An enhanced channel estimation technique for CDD OFDM system over time varying channels. Cluster Comput 22 (Suppl 5), 12069–12075 (2019). https://doi.org/10.1007/s10586-017-1556-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10586-017-1556-2