Skip to main content

Advertisement

SpringerLink
Log in

Statistical modeling of extreme value behavior in North American tree-ring density series

  • Published:
Climatic Change Aims and scope Submit manuscript

Abstract

Many analyses of the paleoclimate record include conclusions about extremes, with a focus on the unprecedented nature of recent climate events. While the use of extreme value theory is becoming common in the analysis of the instrumental climate record, applications of this framework to the spatio-temporal analysis of paleoclimate records remain limited. This article develops a Bayesian hierarchical model to investigate spatially varying trends and dependencies in the parameters characterizing the distribution of extremes of a proxy data set, and applies it to the site-wise decadal maxima and minima of a gridded network of temperature sensitive tree ring density time series over northern North America. The statistical analysis reveals significant spatial associations in the temporal trends of the location parameters of the generalized extreme value distributions: maxima are increasing as a function of time, with stronger increases in the north and east of North America; minima are significantly increasing in the west, possibly decreasing in the east, and exhibit no changes in the center of the region. Results indicate that the distribution varies as a function of both space and time, with tree ring density maxima becoming more extreme as a function of time and minima having diverging temporal trends, by spatial location. Results of this proxy-only analysis are a first step towards directly reconstructing extremal climate behavior, as opposed to mean climate behavior, by linking extremes in the proxy record to extremes in the instrumental record.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

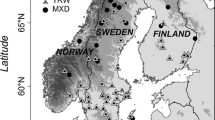
  1. Data currently available at www.cru.uea.ac.uk/∼timo/datapages/mxdtrw.htm.

  2. To address the appropriateness of a GEV distribution for the decadal maxima and minima, we repeated the following exploratory analysis over blocks of 15 years—the results (omitted), are similar to those obtained for decadal extremes.

  3. http://www.ral.ucar.edu/~ericg/softextreme.php

References

  • Banerjee S (2005) On geodetic distance computations in spatial modeling. Biometrics 61:617–625

    Article  Google Scholar 

  • Banerjee S, Carlin BP, Gelfand AE (2004) Hierarchical modeling and analysis for spatial data. Chapman and Hall, Boca Raton, Florida

    Google Scholar 

  • Barriopedro D, Fischer EM, Luterbacher J, Trigo RM, Garcia-Herrera R (2011) The hot summer of 2010: redrawing the temperature record map of Europe. Science 332:220–224

    Article  Google Scholar 

  • Briffa KR, Osborn TJ, Schweingruber FH, Jones PD, Shiyatov SG, Vaganov EA (2002a) Tree-ring width and density data around the northern hemisphere: Part 1, local and regional climate signals. Holocene 6:737–757

    Article  Google Scholar 

  • Briffa KR, Osborn TJ, Schweingruber FH, Jones PD, Shiyatov SG, Vaganov EA (2002b) Tree-ring width and density data around the northern hemisphere: Part 2, spatio-temporal variability and associated climate patterns. Holocene 6:759–789

    Article  Google Scholar 

  • Brohan P, Kennedy JJ, Harris I, Tett SFB, Jones PD (2006) Uncertainty estimates in regional and global observed temperature changes: a new data set from 1850. J Geophys Res 2:99–113

    Google Scholar 

  • Coles S (2001) An introduction to statistical modeling of extreme values. Springer, New York

    Google Scholar 

  • Cooley D, Naveau P, Jomelli V (2006) A Bayesian hierarchical extreme value model for lichenometry. Environmetrics 17:555–574

    Article  Google Scholar 

  • Cooley D, Sain SR (2011) Spatial hierarchical modeling of precipitation extremes from a regional climate model. J Agric Biol Environ Stat 15:381–402

    Article  Google Scholar 

  • de Haan L, Ferreira A (2006) Extreme value theory: an introduction. Springer, Berlin

    Google Scholar 

  • Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B Stat Methodol 39:1–38

    Google Scholar 

  • Evans MN, Reichert BK, Kaplan A, Anchukaitis KJ, Vaganov EA, Hughes MK, Cane MA (2006) A forward modeling approach to paleoclimatic interpretation of tree-ring data. J Geophys Res 111:G03008

    Article  Google Scholar 

  • Field CB, Barros V, Stocker TF, Qin D, Dokken DJ, Ebi KL, Mastrandrea MD, Mach KJ, Plattner GK, Allen SK, Tignor M, Midgley PM (eds) (2012) Managing the risks of extreme events and disasters to advance climate change adaptation—a special report of working groups I and II of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, UK and New York, NY, USA

    Google Scholar 

  • Finkenstädt B, Rootzén H (2004) Extreme values in finance, telecommunication and the environment. Chapman and Hall, Boca Raton, Florida

    Google Scholar 

  • Fotheringham AS, Brunsdon C, Charlton M (2002) Geographically weighted regression: the analysis of spatially varying relationships. Wiley, West Sussex

    Google Scholar 

  • Gelfand AE, Kim H, Sirmans CF, Banerjee S (2003) Spatial modeling with spatially varying coefficient processes. J Am Stat Assoc 98:387–396

    Article  Google Scholar 

  • Gelman A, Carlin JB, Stern HS, Rubin DB (2004) Bayesian data analysis, 2nd edn. Chapman and Hall/CRC, Boca Raton, FL

    Google Scholar 

  • Hsu J (1996) Multiple comparisons: theory and methods. Chapman and Hall, Boca Raton, Florida

    Google Scholar 

  • IPCC (2001) Climate change 2001: the physical science basis. Contribution of working group I to the 3rd assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, UK and New York, NY, USA

    Google Scholar 

  • IPCC (2007) Climate change 2007: the physical science basis. Contribution of working group I to the 4th assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, UK and New York, NY, USA

    Google Scholar 

  • Jones PD, Briffa KR, Osborn TJ, Lough JM, van Ommen TD, Vinther BM, Luterbacher J, Wahl ER, Zwiers FW, Mann ME et al (2009) High-resolution palaeoclimatology of the last millennium: a review of current status and future prospects. Holocene 19:3

    Article  Google Scholar 

  • Katz RW (2010) Statistics of extremes in climate change. Clim Change 100:71–76

    Article  Google Scholar 

  • Katz RW, Brush GS, Parlange MB (2005) Statistics of extremes: modeling ecological disturbances. Ecology 86:1124–1134

    Article  Google Scholar 

  • Kaufman DS, Schneider DP, McKay NP, Ammann CM, Bradley RS, Briffa KR, Miller GH, Otto-Bliesner BL, Overpeck JT (2009) Recent warming reverses long-term arctic cooling. Science 325:1236–1239

    Article  Google Scholar 

  • Kharin VV, Zwiers FW (2000) Changes in the extremes in an ensemble of transient climate simulations with a coupled atmosphere-ocean GCM. J Clim 13:3760–3788

    Article  Google Scholar 

  • Kharin VV, Zwiers FW (2005) Estimating extremes in transient climate change simulations. J Clim 18:1156–1173

    Article  Google Scholar 

  • Li B, Nychka DW, Ammann CM (2007) The “hockey stick” and the 1990s: a statistical perspective on reconstructing hemispheric temperatures. Tellus A 59:591–598

    Article  Google Scholar 

  • Li B, Nychka DW, Ammann CM (2010) The value of multi-proxy reconstruction of past climate. J Am Stat Assoc 105:883–911

    Article  Google Scholar 

  • Little RJA, Rubin DB (2002) Statistical analysis with missing data, 2nd edn. Wiley, New York

    Google Scholar 

  • Luterbacher J, Dietrich D, Xoplaki E, Grosjean M, Wanner H (2004) European seasonal and annual temperature variability, trends, and extremes since 1500. Science 303:1499–1503

    Article  Google Scholar 

  • Mann ME, Bradley RS, Hughes MK (1999) Northern hemisphere temperatures during the past millennium: inferences, uncertainties, and limitations. Geophys Res Lett 26:759–762

    Article  Google Scholar 

  • Mann ME, Rutherford S, Wahl E, Ammann C (2007) Robustness of proxy-based climate field reconstruction methods. J Geophys Res 112:D12109

    Article  Google Scholar 

  • Mann ME, Zhang Z, Hughes MK, Bradley RS, Miller SK, Rutherford S, Ni F (2008) Proxy-based reconstructions of hemispheric and global surface temperature variations over the past two millennia. Proc Natl Acad Sci 105:13252–13257

    Article  Google Scholar 

  • Mann ME, Zhang Z, Rutherford S, Bradley RS, Hughes MK, Shindell D, Ammann C, Faluvegi G, Ni F (2009) Global signatures and dynamical origins of the little ice age and medieval climate anomaly. Science 326(5957):1256–1260

    Article  Google Scholar 

  • Mannshardt-Shamseldin EC, Smith RL, Sain SR, Mearns LO, Cooley D (2010) Downscaling extremes: a comparison of extreme value distributions in point-source and gridded precipitation data. Ann Appl Stat 4:484–502

    Article  Google Scholar 

  • McShane BB, Wyner AJ (2011) A statistical analysis of multiple temperature proxies: are reconstructions of surface temperatures over the last 1000 years reliable? See also the accompanying editorial by Michael Stein, discussions, and rejoinder. Ann Appl Stat 5:5–44

    Article  Google Scholar 

  • Naveau P, Ammann CM (2005) Statistical distributions of ice core sulfate from climatically relevant volcanic eruptions. Geophys Res Lett 32(L05711). doi:10.1029/2004GL021732

  • NRC (2006) Surface Temperature Reconstructions for the Last 2000 Years. National Academies Press, Washington, DC

    Google Scholar 

  • R Development Core Team (2011) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org

  • Resnick SI (2007) Heavy-tail phenomena. Probabilistic and statistical modeling. Springer, New York

    Google Scholar 

  • Rutherford S, Mann ME, Osborn TJ, Bradley RS, Briffa KR, Hughes MK, Jones PD (2005) Proxy-based northern hemisphere surface temperature reconstructions: sensitivity to method, predictor network, target season, and target domain. J Clim 18(13):2308–2329

    Article  Google Scholar 

  • Sang H, Gelfand AE (2009) Hierarchical modeling for extreme values observed over space and time. Environ Ecol Stat 16:407–426

    Article  Google Scholar 

  • Schliep E, Cooley D, Sain SR, Hoeting J (2010) A comparison study of extreme precipitation from six different regional climate models via spatial hierarchical modeling. Extremes 13:219–239

    Article  Google Scholar 

  • Simkin T, Siebert L (1994) Volcanoes of the world: a regional directory, gazeteer and chronology of volcanism during the last 10,000 years, 2nd edn. Global Volcanism Program. Smithsonian Institution, Washington, DC, p 348. Table 2 downloaded from ftp.ncdc.noaa.gov/pub/data/paleo/treering/reconstructions/n_hem_temp/nhemtemp_data.txt

  • Tingley MP (2009) A Bayesian approach to reconstructing space-time climate fields from proxy and instrumental time series, applied to 600 years of northern hemisphere surface temperature data. PhD thesis, Department of Earth and Planetary Sciences, Harvard University, Cambridge, MA. Available at www.martintingley.com

  • Tingley MP, Huybers P (2010a) A Bayesian algorithm for reconstructing climate anomalies in space and time. Part 1: Development and applications to paleoclimate reconstruction problems. J Clim 23:2759–2781

    Article  Google Scholar 

  • Tingley MP, Huybers P (2010b) A Bayesian algorithm for reconstructing climate anomalies in space and time. Part 2: Comparison with the regularized expectation-maximization algorithm. J Clim 23:2782–2800

    Article  Google Scholar 

  • Tingley MP, Craigmile PF, Haran M, Li B, Mannshardt-Shamseldin E, Rajaratnam B (2012) Piecing together the past: statistical insights into paleoclimatic reconstructions. Quat Sci Rev 35:1–22

    Article  Google Scholar 

  • Zwiers FW, Kharin VV (1998) Changes in the extremes of the climate simulated by CCC GCM2 under CO2 doubling. J Clim 11:2200–2222

    Article  Google Scholar 

Download references

Acknowledgements

This collaboration was formed during the 2009–2010 Program on Space-time modeling for Epidemiology, Climate Change, and Environmental Mapping, organized by the Statistical and Applied Mathematical Sciences Institute and supported by the National Science Foundation (NSF) under Grant DMS-0635449. ECM is supported in part by The Program in Spatial Statistics and Environmental Statistics at The Ohio State University. PFC is supported in part by the NSF under grants DMS-0604963, DMS-0906864 and SES-1024709, and MPT by the NSF under Grants ATM-0724828 and ATM-0902374. We thank Peter Guttorp, Richard Smith, Michael Stein, an Associate Editor, and three anonymous reviewers for suggestions that improved this work.

Author information

Authors and Affiliations

  1. Department of Statistics, North Carolina State University, Raleigh, NC, 27695-8203, USA

    Elizabeth Mannshardt

  2. Department of Statistics, Ohio State University, Columbus, OH, 43210-1247, USA

    Peter F. Craigmile

  3. School of Mathematics and Statistics, University of Glasgow, Glasgow, Scotland

    Peter F. Craigmile

  4. Department of Earth and Planetary Sciences, Harvard University, Cambridge, MA, 02138, USA

    Martin P. Tingley

Authors
  1. Elizabeth Mannshardt
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Peter F. Craigmile
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Martin P. Tingley
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Elizabeth Mannshardt.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.

(PDF 312 KB)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mannshardt, E., Craigmile, P.F. & Tingley, M.P. Statistical modeling of extreme value behavior in North American tree-ring density series. Climatic Change 117, 843–858 (2013). https://doi.org/10.1007/s10584-012-0575-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10584-012-0575-5

Keywords

Search

Navigation