Abstract
The doublet C4 peaks at ~ 85 and ~ 89 ppm in solid-state 13C NMR spectra of native cellulose have been attributed to signals of C4 atoms on the surface (solvent-exposed) and in the interior of microfibrils, designated as sC4 and iC4, respectively. The relative intensity ratios of sC4 and iC4 observed in NMR spectra of cellulose have been used to estimate the degree of crystallinity of cellulose and the number of glucan chains in cellulose microfibrils. However, the molecular structures of cellulose responsible for the specific surface and interior C4 peaks have not been positively confirmed. Using density functional theory (DFT) methods and structures produced from classical molecular dynamics simulations, we investigated how the following four factors affect 13C NMR chemical shifts in cellulose: conformations of exocyclic groups at C6 (tg, gt and gg), H2O molecules H-bonded on the surface of the microfibril, glycosidic bond angles (Φ, Ψ) and the distances between H4 and HO3 atoms. We focus on changes in the δ13C4 value because it is the most significant observable for the same C atom within the cellulose structure. DFT results indicate that different conformations of the exocyclic groups at C6 have the greatest influence on δ13C4 peak separation, while the other three factors have secondary effects that increase the spread of the calculated C4 interior and surface peaks.
Similar content being viewed by others
Introduction
Plant cell walls (PCWs) are the most abundant renewable source of carbohydrates on Earth (Duchesne and Larson 1989). PCWs are sophisticated assemblies of cellulose, hemicellulose, pectin and glycoproteins. Even though the components of PCWs have been well studied, there is still limited understanding of the 3D architecture (Cosgrove 2001, 2014; Wang and Hong 2016). This lack of understanding is largely attributed to the complex nature of the interactions between cellulose and other PCW components. Since the first two high-resolution solid-state NMR studies of cellulose were published in 1980 (Atalla et al. 1980; Earl and VanderHart 1980), solid-state NMR spectroscopy has been an important tool in the study of the 3D architecture of PCWs. Solid-state NMR spectroscopy not only revealed the polymorphic structure of cellulose but also detailed the interactions between cellulose and other macromolecules in intact plant cell walls (Dick-Pérez et al. 2011; Earl and VanderHart 1981; Larsson et al. 1999; Newman and Hemmingson 1995; Wang and Hong 2016; Wang et al. 2016a).
Solid-state NMR spectroscopy of cellulose produces doublet δ13C4 peaks that have been used to estimate the degree of crystallinity of cellulose as well as the number of glucan chains in elementary cellulose microfibrils (Kennedy et al. 2007; Newman et al. 1994, 1996; Park et al. 2009; Teeäär et al. 1987; Wang et al. 2015). Two δ13C4 peaks, centered at ~ 89 and ~ 85 ppm, have been assigned to ordered (crystalline) and disordered (amorphous) regions, respectively (Atalla et al. 1980; Earl and VanderHart 1980). This assignment was based on the dominance of 89-ppm signals in highly crystalline cellulose and was tested by ball-milling microcrystalline cellulose sample which led to increased intensity of the 85 ppm peak and a simultaneous decrease in the intensity of the 89 ppm peak (Maciel et al. 1982). The two peaks have also been assigned as the signals from solvent-exposed and interior chains, respectively (Ha et al. 1998; Newman 1998). The intensity ratio between these two peaks gives information about the number of chains in the microfibril, which is consistent with the results obtained from diffraction methods and absorption spectroscopy, which collectively constrain the cross-sectional dimension of cellulose microfibrils (Fernandes et al. 2011). However, the molecular structures of cellulose responsible for the specific surface and interior C4 peaks have not been positively confirmed.
This study examines the role that structural factors could play in changing δ13C4 values using Density Functional Theory (DFT) and structures produced via classical MD simulations. Suzuki et al. (2009) have applied DFT calculations on monosaccharide and disaccharide models in vacuum to demonstrate that 13C4 NMR chemical shifts can be influenced by conformations of exocyclic groups at C6 (tg, gt and gg), glycosidic bond angles (Φ, Ψ) as well as the H atom at the γ-C OH position (C3). However, monosaccharide and disaccharide models differ greatly from a cellulose microfibril and as a result there were significant differences (~ 10 ppm) between the calculated and observed δ13C values. For example, compared to the cellulose experimental δ13C4 values of 79–93 ppm (Park et al. 2009), their calculated δ13C4 were between ~ 65 and ~ 75 ppm. To improve the agreement between observation and calculation, in the work presented here, we utilized an Iβ cellulose model system containing 12 cellotetraose chains with three different conformations of the C6 exocyclic group (tg, gt and gg) as shown in Fig. 1 (Wang et al. 2016b; Watts et al. 2014). The atomic positions of these models had previously been energy-minimized using DFT under periodic boundary conditions (Kubicki et al. 2013). The cellulose model used here is merely a minimal structure that contains both interior (two) and surface (ten) cellulose chains and is of a size that is computationally practical for DFT calculations. It is not intended to suggest that a cellulose microfibril contains only twelve chains. In our previous work, by using Iβ (110) and Iβ (100) surface models, we demonstrated that H2O molecules affected the calculated δ13C4 values of glucose residues with tg conformation (Kubicki et al. 2014). In this paper, using both DFT and classical structures, we investigated how the following four factors affect C4 NMR chemical shifts: conformations of exocyclic groups at C6 (tg, gt and gg), H2O molecules H-bonded to the surface, glycosidic bond angles (Φ, Ψ) and the position of the proton (HO3) of the OH group connected to the adjacent carbon C3. The effect of each factor on δ13C4 was quantified using the computational protocol from our previous work (Kubicki et al. 2013).
Solvated cellulose Iβ models with three different conformations of the C6 exocyclic group (tg, gt and gg, respectively). Each model was produced to be three chains wide, four layers high and four monomer units in length, and was solvated with explicit H2O molecules. The middle two glucan units in the shaded regions represent the cellulose interior while all other glucan units are either surface or terminal. Only H2O within 3 Å of the cellulose cluster (as shown in blue) were included in the following NMR shielding tensor calculations. Bottom: the tg, gt and gg conformers refer to the trans- and gauche states of the dihedral angle O5–C5–C6–O6 and C4–C5–C6–O6, O5 O6 were colored in red and C4 was colored in grey. (Color figure online)
Method
As shown in Fig. 1, cellulose Iβ models with three different conformations of the C6 exocyclic group (tg, gt and gg) were created based on X-ray and neutron diffraction structures of cellulose (Nishiyama et al. 2002). The atomic positions of these models have been previously energy minimized with periodic DFT-D2 calculations (Kubicki et al. 2013, 2014; Watts et al. 2014). As described previously, clusters were produced to be three chains wide, four layers high and four monomer units in length (Wang et al. 2016b), designated as the 4 × 3 × 4 cluster hereafter. This allows for four glucan monomers to have at least one other unit next to them in all three dimensions to represent the atomic environment within cellulose. The middle two glucan units in each chain were used to represent interior 13C NMR chemical shifts. The O4 at the non-reducing end and C1 at the reducing end were terminated with –CH3 and –OCH3 groups, respectively, to satisfy the bonding of the terminal atoms.
Using the Impact module of Maestro (Schrödinger 2014), we solvated the cellulose clusters with TIP3P water (Jorgensen et al. 1983) in a 50 × 50 × 40 Å3 box containing about 3000 H2O molecules. Energy minimizations and molecular dynamics simulations were performed using the OPLS_2005 force field (Banks et al. 2005) keeping the atomic positions of cellulose molecules fixed. 1000 steps of conjugate gradient minimization were performed before 10 ps molecular dynamics simulations at 298 K with a 1 fs time step in the NVT ensemble. In addition to the 4 × 3 × 4 cellulose clusters, H2O molecules were included in the NMR shielding tensor calculations. Only H2O molecules within 3 Å of the cellulose clusters were included as it was found that H2O molecules further than 3 Å from the clusters had negligible effects on the calculated δ13C.
Larger models were impractical due to the total memory usage limit (256 GB) on the computing server. In order to test the sensitivity of the calculated NMR chemical to the size of the cellulose models, relatively smaller 3-layer cellulose models were generated, as shown in supplementary Fig. S1. NMR chemical shifts calculated from 3-layer and 4-layer models are highly consistent to each other, as shown in supplementary Table S1, indicating that the size of our cellulose model (4 × 3 × 4 cellulose clusters) will not affect the quality of the cellulose 13C NMR predictions. Hence, 4 × 3 × 4 cellulose clusters were deemed suitable to study the effects of the aforementioned structural factors on the NMR chemical shifts of cellulose. However, comparing to native cellulose microfibrils from primary cell walls, there are still many other factors that could potentially influence 13C NMR that this current cellulose model (4 × 3 × 4 cellulose clusters) cannot account for, such as cellulose microfibril bundling, and interactions with other matrix polymers.
Rotating glycosidic bonds and torsion angle χ3 (C2–C3–O3–HO3)
To assess the effect of different glycosidic bond angles (Φ: O5′–C1′–O–C4, Ψ: C1′–O–C4–C5) on the 13C NMR chemical shifts, a rigid potential energy surface (PES) scan was performed in Φ/Ψ space on a 7 × 7 grid with a step size of 10°, where − 123.2 ≤ Φ ≤ − 63.2 and − 183.2 ≤ Ψ ≤ − 123.2, using M06-2X/6-31G(d) method (Rassolov et al. 2001; Zhao and Truhlar 2008) in Gaussian 09 (Frisch et al. 2010), a reliable method that has been applied constantly to obtain reasonable molecular structures for organic molecules (Fradon et al. 2017; Khansari et al. 2017; Zhao and Truhlar 2008; Zhou et al. 2017). Forty-nine cellulose tetramer chain conformations with different Φ/Ψ angles were generated for each C6 conformers (gg: C4–C5–C6–O6 = 57.2°; gt: C4–C5–C6–O6 = 178.1°; tg: C4–C5–C6–O6 = 285.7°). Those conformations were then subjected to NMR shielding tensor calculations.
To assess the effect of the position of HO3 on δ13C4, a rigid PES scan was also performed on torsion angle χ3 (C2–C3–O3–HO3) of a cellulose tetramer chain with three different conformations of the C6 exocyclic group (gg: C4–C5–C6–O6 = 57.2°; gt: C4–C5–C6–O6 = 178.1°; tg: C4–C5–C6–O6 = 285.7°) from models being energy minimized previously with periodic DFT-D2 calculations. Torsion angle χ3 was rotated through 360° with a step of 10° using the M06-2X/6-31G(d) method in Gaussian 09. Cellulose tetramer chain conformations generated with different torsion angle χ3 values were then subjected to NMR shielding tensor calculations.
NMR shielding tensor calculations
NMR shielding tensors were calculated as described previously (Kubicki et al. 2013). This protocol has been shown to achieve an RMS error of better than 3 ppm for cellulose Iβ and Iα (Kubicki et al. 2013; Toukach and Ananikov 2013; Wang et al. 2016b). The modified Perdue–Wang exchange–correlation functional mPW1PW91 (Adamo and Barone 1998) with the 6-31G(d) basis set (Rassolov et al. 2001) and gauge-independent atomic orbitals (GIAO) (Bühl et al. 1999; Cheeseman et al. 1996; Karadakov 2006; Lodewyk et al. 2011; Schreckenbach and Ziegler 1995; Wiitala et al. 2006; Wolinski et al. 1990) method in Gaussian 09 were used. Chemical shifts were calculated using the multi-reference method. Methanol was the secondary standard to calculate the 13C chemical shift, because it produces δ13C in better agreement with experiment (Kubicki et al. 2013, 2014; Sarotti and Pellegrinet 2009; Watts et al. 2011, 2014). An empirical correction of 49.5 ppm (Gottlieb et al. 1997) was used for the difference between the δ13C in methanol and TMS commonly used as an experimental 13C NMR standard (Sarotti and Pellegrinet 2009).
This gives an isotropic chemical shielding of 193.0 ppm. To compute the δ13C for any C nucleus i in cellulose, we used:
Results and Discussion
Different conformations of exocyclic groups at C6 (tg, gt and gg)
The interior cellulose chains were used to assess the effects that different conformations of exocyclic groups at C6 (tg, gt and gg conformation) had on the δ13C in cellulose Iβ. Average calculated chemical shifts for each conformation of exocyclic groups at C6 are presented in Table 1. The largest effect was observed on the δ13C4 (Table 1), where, compared to the tg conformation, gt and gg conformations shifted δ13C4 upfield by ~ 1.4, and ~ 6.9 ppm, respectively. Given the moderate standard deviations, the C4 peaks from tg and gt conformations would be indistinguishable within computational error whereas those from gg are outside expected model uncertainties. Consistent with previous results, the gt and gg conformations of C6 shifted the δ13C6 by relatively large values upfield compared to the tg conformation (3 and 3.8 ppm, respectively). This is in good agreement with the CP-MAS NMR experimental finding by Horri et al. (1983) that gg, gt and gt conformations have incremental δ13C6 values of 60–62.6, 62.5–64.5, 65.5–66.5 ppm, respectively. Considering the relatively small standard deviations (0.6 and 0.8 ppm, respectively), these signals are distinguishable from the tg conformer, yet it would be difficult to discern the gt from the gg signal (as observed experimentally where these two peaks are merged).
δ13C1 for the gt and gg conformations were upfield shifted by ~ 2 ppm compared to the tg conformation, however, the standard deviations were of a higher magnitude and therefore, it was not possible to distinguish between δ13C1 with different C6 conformations. This could explain why the peak separation at the C1 region of 13C NMR spectrum only happens within a small chemical shift range of 2 ppm (Jorgensen et al. 1983; Wang et al. 2016b). Similarly, the 13C2 and 13C5 chemical shifts were shifted by ~ 2 ppm for gt and gg conformations, compared to the tg conformation, though downfield. Despite the standard deviations being reduced compared to the 13C1 chemical shifts, it would be difficult to distinguish the peaks resulting from the different C6 conformations, and also from each other. Interestingly, the changing C6 conformations had a negligible effect on the 13C3 chemical shifts, and these peaks would also merge with the 13C2 and 13C5 chemical shifts in an experimental spectrum.
Effects of H2O H-bonding on the surface
Two sets of NMR calculations were conducted on each 4 × 3 × 4 clusters with three different conformations of the C6 exocyclic group (tg, gt and gg) to investigate the effect of changing C6 conformation for surface chains, and of H2O H-bonding. One set of NMR calculation was conducted with H2O molecules to mimic the cellulose microfibril in contact with water while the other set was conducted without any solvent molecules (in vacuum/gas state), to represent the cellulose microfibril in a dried state. In order to compare how these two conditions would affect 13sC NMR chemical shifts (sC: C on the surface), we averaged the calculated chemical shifts at surface chains for each conformation of exocyclic groups at C6, as shown in supplementary Tables S2 and S3. We found that surface chains in a vacuum environment/dried state had downfield shifted δ13sC4 (by ~ 1–2 ppm), compared to interior chains. On the contrary, H2O molecules cause an upfield shift (1 ± 1 ppm) in all 13sC NMR chemical shifts except for δ13sC4. For different C6 conformations δ13sC4 values could be shifted either upfield or downfield depending on hydration (Table 2). We emphasize that the standard deviations in these averages are significant which means that the individual δ13sC4 values could differ by 3–4 ppm from the δ13sC4 values (e.g., tg(s) − tg(i) 1.5 ± 1.7 = 3.2 ppm). Consequently, dehydration of cellulose could mimic tg to gt rotations as far as the δ13sC4 is concerned.
Focusing on the surface chains, the two adjacent surface C4 atoms have similar chemical environment (Oehme et al. 2015), however the C4–H4 group of adjacent glucose units point in opposite directions (Fig. 2). One points towards the solvent environment (designated as C4H4-out), whereas the other points away from the solvent environment to the interior cellulose microfibril (designated as C4H4-in). We found that hydration had relative large effects on δ13sC4H4-out, yet negligible effects on δ13sC4H4-in. Water molecules upfield shifted δ13sC4H4-out of gg and gt conformers by ~ 2 and ~ 1.3 ppm, respectively. On the contrary, δ13sC4H4-in values of gg and gt conformers were either downfield shifted by ~ 0.9 ppm or upfield shifted by only ~ 0.1 ppm respectively. A vacuum environment had the opposite effects on 13sC NMR chemical shifts of C4H4-out moving them downfield, whereas C4H4-in, was affected in a similar manner to water-solvated chains. Directly comparing the δ13sC4 with or without water solvent (last column of Table 2), we found that H4-out residues demonstrated much more significant chemical shift perturbation than H4-in residues did. This indicates that two adjacent C4 on the surface have different chemical environment with the C4 having its H4 pointing into the interior behaving like an interior C4, and only every other glucose δ13sC4 is effected by H-bonding to water.
Averaging chemical shifts over all C atoms has the effect of ignoring key contributions that could be made by individual carbons. Previous work has shown that H-bonding from H2O molecules to C4 had a significant effect (Kubicki et al. 2014). By examining individual glucose residues, we found that several δ13C4 on the surface were downfield shifted by ~ 4–5 ppm due to the absence of H-bonding (H–O < 2.5 Å and O–H–O > 90°) (Kubicki et al. 2014) to H2O molecules. This is comparable to the findings in Kubicki et al. (2014) and also explained the relative large standard deviations observed when the δ13C4 are averaged.
Glycosidic bond angles (Φ Ψ)
Other factors that have been suggested to affect δ13C4 are the Φ and Ψ dihedral angles (Φ: O5′–C1′–O–C4; Ψ: C1′–O–C4–C5; SI Fig. 1). The Φ and Ψ angles in the 4x3x4 clusters represent the glycosidic bond angles at the region of conformational minimum (Wang et al. 2016b), because the clusters were generated based on the X-ray and neutron diffraction structures of cellulose and energy minimized with periodic DFT-D2 calculations (Kubicki et al. 2013, 2014). However, it is unrealistic to think that all the Φ and Ψ angles in a biological sample would be at the conformational minimum. To obtain a more realistic distribution of Φ and Ψ angles in a cellulose microfibril, the final structure from a MD simulation on an 18-chain Iβ cellulose microfibril model, published by Oehme et al. 2015, has also been utilized. To assess the dependence of δ13C4 on the glycosidic dihedral angles (Ψ, Φ), a rigid potential energy surface scan was conducted on Φ and Ψ, where − 123.2° ≤ Φ ≤ − 63.2° and − 183.2° ≤ Ψ ≤ − 123.2°. The relative energies of the rigid PES scan and the distribution of Φ and Ψ angles obtained from MD simulations were plotted together in Fig. 3a. There was good agreement between allowed Φ/Ψ angles observed from MD simulations and the relative energies obtained from the rigid PES scan. As shown in Fig. 3a, almost all the allowed Φ/Ψ angles observed from the MD simulation were clustered into the low-energy zone, with relative potential energies no more than 20 kJ/mol above the minimum. The Φ/Ψ angles at the minimum were consistent with those angles in the 4 × 3 × 4 clusters as well as those angles in the X-ray crystal structure of cellulose Iβ, as shown in Fig. 3b.
a Overlapping the energy contour map of relative energies of cellotetramer (with C6 exocyclic groups at tg conformation) when rotating the glycosidic linkage dihedral angles Φ and Ψ with the observed dihedral angles Φ and Ψ from MD simulation, white triangles represent Φ/Ψ from surface chains in MD simulation, yellow squares represent Φ/Ψ from surface chains in MD simulation; b overlay of the contour map with the table of calculated relative δ13C4 values for different dihedral angles Φ and Ψ. The regions where dihedral angles Φ and Ψ are observed in MD simulations are in grey dashed line square. The yellow dashed line square represented the crystalline conformational minimum (when Ψ = − 143° ± 10° and Φ = − 93° ± 10°). The three black dots represent the Φ/Ψ angles in the 4 × 3 × 4 clusters, − 85°/− 155°, − 92°/− 150° and − 94°/− 145° for gg, gt and tg, respectively. The two black triangles represent the Φ/Ψ angles from the X-ray structure of cellulose Iβ by Nishiyama et al. (2003). (Color figure online)
The allowed Φ/Ψ angles observed from the MD simulation (− 163° ≤ Ψ ≤ − 133° and − 113° ≤ Φ ≤ − 83°) were plotted overlapped with the calculated relative δ13C4 values, as shown in Fig. 3b, to estimate the effect of the allowed the Φ/Ψ angles on δ13C4. Using the DFT minimized tg conformation as a reference, the allowed Φ/Ψ angles observed from MD simulations caused an upfield shift in δ13C4 by up to 1.3 ppm in interior chains, and a more diverse shift of up to 5.7 ppm in surface chains.
In addition, when the C6 was in the gt or gg conformation, rotation about the glycosidic bond had a similar effect on δ13C4. As shown in Supplementary Table S4 and S5, the allowed Φ/Ψ angles observed from MD simulations caused an upfield shift in δ13C4 by up to 1.6 ppm (gg) and 1.4 ppm (gt) in interior chains, and a more diverse shift of up to 6.0 ppm (gg) and 6.4 ppm (gt) in surface chains.
δ13C for the adjacent glucose units connected by the glycosidic bond of interest were also calculated, as shown in the supplementary materials (Supplementary Table S6). In addition to δ13C4, only δ13C1 and δ13C2 are appreciably influenced by the rotation about the glycosidic bond. As shown in Supplementary Table S6, using the DFT minimized tg conformation as the reference, δ13C1 and δ13C2 can be upfield shifted by up to ~ 3.8 ppm or downfield shifted by up to ~ 1.3 ppm. The rotation about the glycosidic bond had negligible effect on δ13C6.
Applying DFT calculations on a cellobiose model, Suzuki et al. (2009) studied the dependence of δ13C4 on the glycosidic Φ or Ψ angles separately. In their study, either Φ or Ψ was rotated in steps of 30° for a full 360° while keeping the other angle fixed. They found that in the region of the crystalline conformational minimum, δ13C4 was dependent on both Φ/Ψ angles, but only δ13C1 and δ13C2 were dependent on Ψ. However, MD simulations demonstrated that both Φ and Ψ angles have the potential to rotate in a cellulose microfibril (Oehme et al. 2015). In this study, together with the allowed Φ/Ψ angles values provided via MD simulations on the 18-chain cellulose microfibril models, our study provided more detailed information of the dependence 13C4 NMR chemical shifts on both Φ/Ψ angles. The effect that rotation about the glycosidic bond had on δ13C4 was independent of the conformation at C6 (gt, gg, tg). In the region of the crystalline conformational minimum (when Ψ = − 143° ± 10° and Φ = − 93° ± 10°), where 100% of the Φ/Ψ angles for interior chains and ~ 60% of them for surface chains in MD simulations were sampled, δ13C4 exhibit limited changes due to the limited variation of Φ/Ψ angles, with at most an upfield shift of ~ 2 ppm, consistent with our previous study (Kubicki et al. 2013). δ13C4 were more sensitive to changes of the Φ/Ψ angles sampled by surface chains in MD simulations; the chemical shifts associated with these angles are upfield shifted by up to ~ 6 ppm.
Effect of adjacent HO3 group
The position of the proton (HO3) of the OH group connected to C3 has also been proposed to influence the 13C4 NMR chemical shift (Suzuki et al. 2009). In order to investigate the relationship between HO3 and the 13C4 NMR chemical shift, a PES, the distance between H4 and HO3, and the 13C4 NMR chemical shift were all calculated for each C6 conformation and are plotted with respect to the HO3–O3/C4–H4 dihedral angle. From the PES, for all C6 conformations there is a global minimum when the HO3–O3/C4–H4 torsion angle is around 100°, which corresponds to a strong inter-residue H-bond forming between O3 and O5 (O5 of the adjacent glucose unit) (Fig. 4, conformation B). Inter-residue H-bond between O3 and O5 has been reported for both Iα and Iβ allomorphs, thus is common to native cellulose (Nishiyama et al. 2002, 2003). All the HO3 protons in the DFT energy minimized 4x3x4 clusters were also found to have the similar position as shown in the conformation B. Additionally, O3 can form a relative weak intra-residue H-bond with O2, which corresponds to a local minimum, when the HO3–O3/C4–H4 torsion angle was around 260° (Fig. 4). However, this minimum is not found for the gg conformation. As shown in supplementary Fig. S3, the gg conformations at C6 causes HO2 to be re-positioned, so the H-bond between O3 and O2 does not form.
Top row, relative potential energies of cellotetramers with respect to different torsion angle HO3–O3/C4–H4 when the exocyclic group at C6 taking tg, gt and gg conformations, respectively; Middle row, distances between H4 and HO3 (shown as circle, primary y-axis) and C4 NMR chemical shifts (shown as black dots, secondary y-axis) in relation to torsion angle HO3–O3/C4–H4.; Bottom row, representative structures of cellulose tetramer of tg conformation at the max δ13C4 (conformation A), plateau/energy minimum (conformation B), and min δ13C4 (conformation C)
13C4 NMR chemical shifts were found to be influenced by the distance between H4 and HO3 (Fig. 4). As the distance between H4 and HO3 increased, δ13C4 decreased, except when the HO3–O3/C4–H4 torsion angle was between 60° and 120°. Here, the δ13C4 plot formed a plateau at around 88, 87 and 80 ppm for tg, gt and gt conformations, respectively, even though the distance between H4 and HO3 increased from about 2.5 to 3.1 Å. This was probably due to strong inter-residue H-bonding between O3–HO3 and O5′ (Fig. 4). When the distance between H4 and HO3 was at a maximum (~ 3.6 Å) with the torsion angle of HO3–O3/C4–H4 at ~ 203°, δ13C4 reached a minimum, upfield shifted by ~ 2 ppm from the plateau. When the distance between H4 and HO3 was at a minimum (~ 2.1 Å) with the torsion angle of HO3–O3/C4–H4 at ~ 200°, δ13C4 reached a maximum, downfield shifted by ~ 3 ppm from the plateau. A similar relationship between δ13C1′ and the torsion angle O22–HO22/C12–H12 was also observed when rotating χ2 (C12C22O22HO22), as shown in supplementary Fig. S4.
Applying DFT calculations on a single glucose (with C6 at gt conformation) model Suzuki et al. (2009) found that 13C4 NMR chemical shift could be influenced by the position of the H (HO3) of the OH group connected to the adjacent carbon C3. They explained this qualitatively as resulting from the γH-gauche effect and intra-residue H-bonds. They found that δ13C4 was higher (75.1 and 77.2 ppm) when HO3 was at gauche position (when torsion angle of C2–C3–O3–HO3 was at 60° or 180°) compared to the δ13C4 value (70.3 ppm) when HO3 was in a trans position (when the torsion angle of C2–C3–O3–HO3 was at 300°). Consistently, we found that δ13C4 was higher (~ 89 and ~ 88 ppm) when HO3 was in the gauche position (C2–C3–O3–HO3 = 60° or 180°), whereas when HO3 was at trans position (C2–C3–O3–HO3 = 300°), δ13C4 was ~ 85 ppm. However, the gauche or trans positions cannot be correlated precisely to the maximum or minimum δ13C4 (when torsion angle of C2–C3–O3–HO3 was at ~ 83° or ~ 282°, respectively), which suggested that this γH-gauche effect provided by Suzuki and co-authors cannot fully account for the effect of HO3 position on δ13C4.
In this study, we found that 13C4 NMR chemical shift had an inverse relationship with the distance between H4 and HO3. The δ13C4 reached a maximum when the distance between H4 and HO3 was shortest and a minimum when furthest apart. Also, the inter-residue H-bond between O3–HO3 and O52 was shown to affect the 13C4 NMR chemical shift, which was not identified in the previous study due to the small size of the model. Our calculated δ13C4 values were in good agreement with the experiment values (79–93 ppm) (Park et al. 2009), which varied from 77 to 90 ppm. Due to the small size of the model from the previous work, their calculated δ13C4 varied from 70 to 75 ppm, ~ 10 ppm lower than the experiment values.
Implications for interpreting observed solid-state 13C NMR spectra of native cellulose in intact cell walls
As shown in Fig. 5, our calculated 13C NMR chemical shifts have a reasonably good agreement with the observed ssNMR spectra of native cellulose inside the intact and native Arabidopsis primary cell wall (Wang and Hong 2016). Since the δ13C4 value is the most significant observable for the same C atom within the cellulose structure, our analysis was focused on changes in the δ13C4 value.
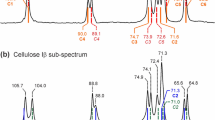
Different conformations of the exocyclic groups at C6 have the greatest influence on δ13C. a Calculated average δ13C1-6 for gg gt and tg conformations by using the three models shown in Fig. 1; b 1D 13C cross polarization (CP) solid-state NMR spectrum of Arabidopsis primary cell wall measured on an 800 MHz spectrometer (Wang et al. 2016b). The cellulose-dominant peaks are labeled in the spectrum
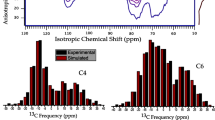
As shown in Fig. 6, considering the effects of different conformation of exocyclic groups at C6, water and vacuum environments on 13C NMR chemical shifts, our calculated δ13C4 were separated into two ‘peaks’, centered at ~ 79 and ~ 86 ppm, respectively. One ‘peak’ at upfield (~ 79 ppm) was dominated by gg conformers, whereas the other one at downfield (~ 86 ppm) was dominated by tg and gt conformers. Although the effect of H2O molecules H-bonding was to shift the gt and tg conformers on the surface upfield, our calculations indicate that these upfield shifts (gt: − 0.6 ± 1.9 ppm, tg: 0.1 ± 1.6 ppm) were not large enough to explain the ‘gap’ in C4 doublet peak (~ 5.5 ppm). In addition to different conformations at C6 and H2O molecules at the surface, δ13C4 were shown to be affected by rotation about the glycosidic bond, and the position of HO3 (the proton of –OH group connected to the adjacent C3). Variation in dihedral angles about the glycosidic bond always caused an upfield shift in the δ13C4. Combining DFT calculations and structures from classical MD simulations, we found that δ13C4 were relatively insensitive (varied by up to ~ 2 ppm) to changes in the Φ/Ψ angles of interior cellulose chains, due to their small variation in the region of crystalline conformational minimum (Ψ = − 143 ± 10o and Φ = − 93 ± 10o) as sampled by MD. In comparison, changes of Φ/Ψ angles of surface cellulose chains could upfield shift δ13C4 by up to around 4.3 ppm. There was an inverse relationship between δ13C4 and the distance between H4 and HO3. When the distance between H4 and HO3 was at a maximum (~ 3.6 Å), δ13C4 reached a minimum (~ 2 ppm upfield shift) while when at a minimum (~ 2.1 Å), δ13C4 reached a maximum, (~ 3 ppm downfield shift). Interestingly, the inter-residue H-bonds between O3–HO3 and O5 or O2 were able to stabilize 13C4 NMR chemical shift, even with the H4–HO3 distance increasing. Therefore, our study indicated that the C4 peak separation was due to a combination of the above four factors, the different conformation at C6, water/gas environment, Φ and Ψ angles, and the position of HO3. However, different conformations of the exocyclic groups at C6 have the greatest influence on δ13C4 peak separation. The other three factors have secondary effects that increase the spread of the calculated C4 interior and surface peaks.
Summary of the effects of different conformation of exocyclic groups at C6 [tg(i), gt(i) and gg(i)], solvent environment (water or gas/vacuum), glycosidic bond angles (Φ/Ψ), and position of HO3 atoms on δ13C4. (i) represents the signals from interior cellulose whereas (s) represents signals from glucose on the surface of cellulose microfibril model. The horizontal error bars are the standard error except for effect of Φ/Ψ and HO3. The horizontal error bars in the effect of Φ/Ψ represented that changes of Φ/Ψ angles of surface cellulose chains could upfield shift δ13C4 by 5.7 (tg), 6.0 (gt) and 6.4(gg) ppm. The horizontal error bars in the effect of HO3 represented the 3 ppm upfield shift or 2 ppm downfield shift due to the distance changing between H4 and HO3
This study was an attempt to interpret solid-state NMR spectra from a structural point of view. The iC4 peak (~ 89 ppm) was found to be dominated by the tg conformation, consistent with the previous finding from Wang et al. 2016a, b using a non-solvated cellulose model, though the gt conformation may also contribute to iC4 peak. For the sC4 peak (~ 85 ppm), two possible substructures could be contributing to the presence of this peak. It is either dominated by the gt conformation, as shown in Fig. 6, when it is further upfield shifted due to rotation about the glycosidic bond and the position of HO3, or it could be dominated by the gg conformation. The gg C4 chemical shift was centered at ~ 79 ppm, which is out of the NMR C4 chemical shift range of 89–84 ppm. Our method cannot totally exclude the possibility that part of sC4 peak is dominated by gg C4, because the protocol we applied here has the RMS error of ~ 3 ppm for cellulose Iβ and Iα (Kubicki et al. 2013; Toukach and Ananikov 2013). However, based on these calculations and analysis, we believe that the gg conformation is the least probable. This may not change the current predominant interpretation of the surface and interior nature of cellulose signals, however it is possible that a portion of cellulose may violate the surface-interior assignment. Therefore interior and surface percentages and crystallinity determined using the doublet δ13C4 peaks may have limited accuracy. Our results still suggest that there is a link between the two peaks and that they can be classified as crystalline or amorphous as it would be expected that amorphous chains would have gg or gt conformation and crystalline will be tg. However, the calculations do suggest that not all amorphous chains will be represented by the upfield peak (~ 85 ppm), and part of the signals from amorphous chains could reside in the downfield peak (~ 89 ppm).
In addition to δ13C4, we also found that δ13C6 values were sensitive to the first two factors, the conformations at C6 and the H2O molecules on the surface. As shown in Fig. 7, the calculated δ13C6 were also separated into two ‘peaks’, centered at ~ 61 and ~ 64 ppm, respectively. The ‘upfield peak’ was dominated by gg and gt conformers, whereas the ‘downfield peak’ was dominated by tg conformers. The calculated results are in good agreement with the observed C6 peaks (centered at ~ 62 and ~ 65 ppm) in solid-state NMR spectra. This confirmed that the percentage of residues with gt and gg conformations can be estimated by calculating the size of the upfield C6 peak, whereas the percentage of residues with tg conformations can be estimated by the size of the downfield C6 peak (Horii et al. 1983; Oehme et al. 2015). In addition, microfibril bundling and intermolecular interactions with matrix polysaccharides, two factors crucial to wall mechanics, may also perturb the NMR chemical shifts of cellulose, thus are of high interest for future studies (Cosgrove 2016a, b).
Summary of the effects of different conformation of exocyclic groups at C6 [tg(i), gt(i) and gg(i)], solvent environment (water or gas/vacuum) on δ13C6. (i) represents the signals from interior cellulose whereas (s) represents signals from glucose on the surface of cellulose microfibril model. The horizontal error bars are the standard error
Conclusion
In this paper, we have studied the structural factors that influence 13C NMR chemical shifts in cellulose using DFT methods. We found that different conformations of the exocyclic groups at C6 (gg, gt and tg conformations) have the greatest influence on δ13C4 peak separation, while other structural factors, such as H2O molecules H-bonded on the surface of the microfibril, glycosidic bond angles (Φ, Ψ) and the distances between H4 and HO3 atoms, have secondary effects that increase the spread of the calculated C4 interior and surface peaks. We concluded that iC4 peak (~ 89 ppm) was dominated by the tg conformation, while sC4 (~ 85 ppm) peak was dominated by either gg or gt conformations. Hence, even though the conventional assignment of two C4 peaks observed by 13C NMR to surface and interior regions may not be accurate; it is still possible that there is a link between the two peaks and that they can be classified as interior/crystalline or surface/amorphous regions.
References
Adamo C, Barone V (1998) Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: the mPW and mPW1PW models. J Chem Phys 108:664–675
Atalla RH, Gast J, Sindorf D, Bartuska V, Maciel G (1980) Carbon-13 NMR spectra of cellulose polymorphs. J Am Chem Soc 102:3249–3251
Banks JL et al (2005) Integrated modeling program, applied chemical theory (IMPACT). J Comput Chem 26:1752–1780
Bühl M, Kaupp M, Malkina OL, Malkin VG (1999) The DFT route to NMR chemical shifts. J Comput Chem 20:91–105
Cheeseman JR, Trucks GW, Keith TA, Frisch MJ (1996) A comparison of models for calculating Nuclear Magnetic Resonance shielding tensors. J Chem Phys 104:5497–5509
Cosgrove DJ (2001) Wall structure and wall loosening. A look backwards and forwards. Plant Physiol 125:131–134
Cosgrove DJ (2014) Re-constructing our models of cellulose and primary cell wall assembly. Curr Opin Plant Biol 22:122–131
Cosgrove DJ (2016a) Catalysts of plant cell wall loosening. F1000Research 5:1
Cosgrove DJ (2016b) Plant cell wall extensibility: connecting plant cell growth with cell wall structure, mechanics, and the action of wall-modifying enzymes. J Exp Bot 67:463–476
Dick-Pérez M, Zhang Y, Hayes J, Salazar A, Zabotina OA, Hong M (2011) Structure and interactions of plant cell-wall polysaccharides by two-and three-dimensional magic-angle-spinning solid-state NMR. Biochemistry 50:989–1000
Duchesne LC, Larson D (1989) Cellulose and the evolution of plant life. Bioscience 39:238–241
Earl WL, VanderHart DL (1980) High resolution, magic angle sampling spinning Carbon-13 NMR of solid cellulose I. J Am Chem Soc 102:3251–3252
Earl WL, VanderHart DL (1981) Observations by high-resolution Carbon-13 Nuclear Magnetic Resonance of cellulose I related to morphology and crystal structure. Macromolecules 14:570–574
Fernandes AN et al (2011) Nanostructure of cellulose microfibrils in spruce wood. Proc Natl Acad Sci 108:E1195–E1203
Fradon A, Cloutet E, Hadziioannou G, Brochon C, Castet F (2017) Optical properties of donor–acceptor conjugated copolymers: a computational study. Chem Phys Lett 678:9–16
Frisch M et al (2010) Gaussian 09, revision B. 01. Gaussian, Inc, Wallingford
Gottlieb HE, Kotlyar V, Nudelman A (1997) NMR chemical shifts of common laboratory solvents as trace impurities. J Organ Chem 62:7512–7515
Ha MA et al (1998) Fine structure in cellulose microfibrils: NMR evidence from onion and quince. Plant J 16:183–190
Horii F, Hirai A, Kitamaru R (1983) Solid-state 13C NMR study of conformations of oligosaccharides and cellulose. Polym Bull 10:357–361
Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML (1983) Comparison of simple potential functions for simulating liquid water. J Chem Phys 79:926–935
Karadakov PB (2006) Ab initio calculation of NMR shielding constants. In: Webb GA (ed) Modern magnetic resonance. Springer, Berlin, pp 63–70
Kennedy CJ, Cameron GJ, Šturcová A, Apperley DC, Altaner C, Wess TJ, Jarvis MC (2007) Microfibril diameter in celery collenchyma cellulose: X-ray scattering and NMR evidence. Cellulose 14:235–246
Khansari ME, Mirchi A, Pramanik A, Johnson CR, Leszczynski J, Hossain MA (2017) Remarkable hexafunctional anion receptor with operational urea-based inner cleft and thiourea-based outer cleft: novel design with high-efficiency for sulfate binding. Sci Rep 7:6032
Kubicki JD, Mohamed MN-A, Watts HD (2013) Quantum mechanical modeling of the structures, energetics and spectral properties of Iα and Iβ cellulose. Cellulose 20:9–23
Kubicki JD, Watts HD, Zhao Z, Zhong L (2014) Quantum mechanical calculations on cellulose–water interactions: structures, energetics, vibrational frequencies and NMR chemical shifts for surfaces of Iα and Iβ cellulose. Cellulose 21:909–926
Larsson PT, Hult E-L, Wickholm K, Pettersson E, Iversen T (1999) CP/MAS 13C-NMR spectroscopy applied to structure and interaction studies on cellulose I. Solid State Nucl Magn Reson 15:31–40
Lodewyk MW, Siebert MR, Tantillo DJ (2011) Computational prediction of 1H and 13C chemical shifts: a useful tool for natural product, mechanistic, and synthetic organic chemistry. Chem Rev 112:1839–1862
Maciel GE, Kolodziejski WL, Bertran MS, Dale BE (1982) Carbon-13 NMR and order in cellulose. Macromolecules 15:686–687
Newman RH (1998) Evidence for assignment of 13C NMR signals to cellulose crystallite surfaces in wood, pulp and isolated celluloses. Holzforschung 52:157–159
Newman RH, Hemmingson JA (1995) Carbon-13 NMR distinction between categories of molecular order and disorder in cellulose. Cellulose 2:95–110
Newman RH, Ha M-A, Melton LD (1994) Solid-state 13C NMR investigation of molecular ordering in the cellulose of apple cell walls. J Agric Food Chem 42:1402–1406
Newman RH, Davies LM, Harris PJ (1996) Solid-state 13C Nuclear Magnetic Resonance characterization of cellulose in the cell walls of Arabidopsis thaliana leaves. Plant Physiol 111:475–485
Nishiyama Y, Langan P, Chanzy H (2002) Crystal structure and hydrogen-bonding system in cellulose Iβ from synchrotron X-ray and neutron fiber diffraction. J Am Chem Soc 124:9074–9082
Nishiyama Y, Sugiyama J, Chanzy H, Langan P (2003) Crystal structure and hydrogen bonding system in cellulose Iα from synchrotron X-ray and neutron fiber diffraction. J Am Chem Soc 125:14300–14306. https://doi.org/10.1021/ja037055w
Oehme DP, Downton MT, Doblin MS, Wagner J, Gidley MJ, Bacic A (2015) Unique aspects of the structure and dynamics of elementary Iβ cellulose microfibrils revealed by computational simulations. Plant Physiol 168:3–17
Park S, Johnson DK, Ishizawa CI, Parilla PA, Davis MF (2009) Measuring the crystallinity index of cellulose by solid state 13C Nuclear Magnetic Resonance. Cellulose 16:641–647
Rassolov VA, Ratner MA, Pople JA, Redfern PC, Curtiss LA (2001) 6–31G* basis set for third-row atoms. J Comput Chem 22:976–984
Sarotti AM, Pellegrinet SC (2009) A multi-standard approach for GIAO 13C NMR calculations. J Organ Chem 74:7254–7260
Schrödinger L (2014) Schrödinger Release 2014-1: Maestro, version 9.7. New York, NY
Schreckenbach G, Ziegler T (1995) Calculation of NMR shielding tensors using gauge-including atomic orbitals and modern density functional theory. J Phys Chem 99:606–611
Suzuki S, Horii F, Kurosu H (2009) Theoretical investigations of 13C chemical shifts in glucose, cellobiose, and native cellulose by quantum chemistry calculations. J Mol Struct 921:219–226
Teeäär R, Serimaa R, Paakkarl T (1987) Crystallinity of cellulose, as determined by CP/MAS NMR and XRD methods. Polym Bull 17:231–237
Toukach FV, Ananikov VP (2013) Recent advances in computational predictions of NMR parameters for the structure elucidation of carbohydrates: methods and limitations. Chem Soc Rev 42:8376–8415
Wang T, Hong M (2016) Solid-state NMR investigations of cellulose structure and interactions with matrix polysaccharides in plant primary cell walls. J Exp Bot 67:503–514
Wang T, Park YB, Daniel JC, Hong M (2015) Cellulose-Pectin spatial contacts are inherent to never-dried Arabidopsis Thaliana primary cell walls: evidence from solid-state NMR. Plant physiology 168:871–884
Wang T, Phyo P, Hong M (2016a) Multidimensional solid-state NMR spectroscopy of plant cell walls. Solid State Nucl Magn Reson 78:56–63
Wang T, Yang H, Kubicki JD, Hong M (2016b) Cellulose structural polymorphism in plant primary cell walls investigated by high-field 2D solid-state NMR spectroscopy and Density Functional Theory calculations. Biomacromolecules 17:2210–2222
Watts HD, Mohamed MNA, Kubicki JD (2011) Comparison of multistandard and TMS-standard calculated NMR shifts for coniferyl alcohol and application of the multistandard method to lignin dimers. J Phys Chem B 115:1958–1970
Watts HD, Mohamed MNA, Kubicki JD (2014) A DFT study of vibrational frequencies and 13C NMR chemical shifts of model cellulosic fragments as a function of size. Cellulose 21:53–70
Wiitala KW, Hoye TR, Cramer CJ (2006) Hybrid density functional methods empirically optimized for the computation of 13C and 1H chemical shifts in chloroform solution. J Chem Theory Comput 2:1085–1092
Wolinski K, Hinton JF, Pulay P (1990) Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J Am Chem Soc 112:8251–8260
Zhao Y, Truhlar DG (2008) The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theoret Chem Acc 120:215–241
Zhou C-C, Hawthorne MF, Houk KN, Jiménez-Osés G (2017) Multiple mechanisms for the thermal decomposition of metallaisoxazolin-5-ones from computational investigations. J Organ Chem 82:8438–8443
Acknowledgments
This work is supported by the Center for Lignocellulose Structure and Formation, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award # DE-SC0001090. Portions of this research were conducted with Advanced Cyber Infrastructure computational resources provided by the Institute for Cyber Science at The Pennsylvania State University (http://ics.psu.edu). This research also used resources of NERSC, supported by the Office of Science of DOE under Contract No. DE-AC02-05CH11231. This work was completed while DPO was at IBM Research Australia.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yang, H., Wang, T., Oehme, D. et al. Structural factors affecting 13C NMR chemical shifts of cellulose: a computational study. Cellulose 25, 23–36 (2018). https://doi.org/10.1007/s10570-017-1549-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10570-017-1549-6