Nonlinear representation of the confidence region of orbits determined on short arcs

Abstract

The total number of active satellites, rocket bodies, and debris larger than 10 cm is currently about 20,000. If all resident space objects larger than 1 cm are considered, this number increases to an estimate of 700,000 objects. The next generation of sensors will be able to detect small-size objects, producing millions of observations per day. However, due to observability constraints, long gaps between observations will be likely to occur, especially for small objects. As a consequence, when acquiring observations on a single arc, an accurate determination of the space object orbit and the associated uncertainty is required. This work aims to revisit the classical least squares method by studying the effect of nonlinearities in the mapping between observations and state. For this purpose, high-order Taylor expansions enabled by differential algebra are exploited. In particular, an arbitrary-order least squares solver is implemented using the high-order expansion of the residuals with respect to the state. Typical approximations of differential correction methods are then avoided. Finally, the confidence region of the solution is accurately characterized with a nonlinear approach, taking advantage of these expansions. The properties and performance of the proposed methods are assessed using optical observations of objects in LEO, HEO, and GEO.

1 Introduction

Since the era of space exploration started, the number of Earth-orbiting objects has on average grown (Liou et al. 2013). A more crowded space environment raises the possibility of satellite collisions, thus seriously threatening the viability of space activities. Tracking and monitoring Earth-orbiting objects is therefore essential. For this purpose, catalogs of as many resident space objects (RSOs) as possible have been built and are continuously maintained. Such catalogs are used to enable safe space operations, e.g., to predict orbital conjunctions (Hobson et al. 2015). The utility and reliability of these catalogs depend on the accuracy and timeliness of the information used to maintain them. Regular and direct observation of RSOs is therefore a crucial source of information to perform orbit determination (OD) and maintain the above-mentioned catalogs. In the OD process, we can differentiate initial orbit determination (IOD) and accurate orbit estimation (AOE). The former is typically employed to estimate the value of all six orbital parameters (the unknowns) from six independent scalar observations (e.g., three pairs of right ascension and declination), when a priori information on the orbit is not available. It is worth noting that some techniques have been developed, which provide an IOD solution even when the processed observations are less than six, as it happens with the admissible region (Milani et al. 2004). However, the orbit is not fully resolved unless some additional constraints are available. The IOD gives a first estimate, and this solution is then used to obtain follow-up observations and refine the OD process. In contrast, the AOE is used to obtain a better estimate of a priori orbital parameters from a large set of tracking data (Montenbruck and Gill 2000). The AOE requires that RSOs be observed on a regular basis and observations belonging to the same object identified. The latter task is known as data association.

Currently, more than 20,000 man-made objects larger than 10 cm in size are tracked by the US space surveillance network (SSN) (Fedrizzi et al. 2012). However, since the size of launched spacecraft is continuously decreasing [e.g., constellations of CubeSats such as Flock 1 or future mega-constellations like OneWeb (Radtke et al. 2017)], RSOs of small dimension will need to be tracked as they can yield catastrophic collisions. Due to observability constraints, observations of such small objects may be characterized by long observational gaps. Thus, a future challenge will be to accurately determine the orbit of the object with a single passage of the object above an observing station, when a short arc is observed. The estimated number of RSOs larger than 1 cm is around 700,000 (Pechkis et al. 2016; Wilden et al. 2016). This large number of objects will turn the data association problem into an even more challenging task. Realistic description of the uncertainties of IOD solutions is required to perform reliable data association, as well as to initialize Bayesian estimators for orbit refinement (Schumacher et al. 2015). However, when the initial orbit solution is based on observations spread over a short arc, only partial information about the curvature of the orbit can be inferred and, thus, the estimated orbit will be affected by a large uncertainty.

One common approach to handle very short arcs is based on attributables and admissible regions (Milani et al. 2004). An attributable is defined as a four-dimensional vector with data acquired from a short arc. In the case of optical observations, an attributable contains two angles (e.g., right ascension and declination) and their angular rates, $\mathcal {A} = (\alpha , \delta , \dot{\alpha }, \dot{\delta })$. Regardless of how many measurements are acquired for a newly observed object, only four quantities are kept in the attributable. The resulting orbit is then undetermined in the range $\rho$, range-rate $\dot{\rho }$ space. The two degrees of freedom of the attributable thus generate the $2D$ plane in which the admissible region lies. The region is bounded by some physical constraints such as semiaxis and eccentricity (DeMars and Jah 2013). For each point in the admissible region, we can define a virtual debris (VD), made of a $(\bar{\rho },\bar{\dot{\rho }})$ pair and an attributable, that defines the admissible region. Because all six components are defined, the VD has a known orbit.

In this work, we focus on observation scenarios in which observations span arc lengths that are long enough to allow us to solve a least squares (LS) problem, but too short to accurately determine the orbits. We refer to this situation as short arc observations (in contrast with too short arc observations, in which an orbit cannot be determined). In this framework, we propose to (1) solve a LS problem using all observations belonging to the same tracklet with an arbitrary-order solver, and (2) nonlinearly characterize the confidence region of the LS solution. Our main objective is thus to shed some light on the effects of nonlinearities resulting from observations on short arcs. Unless differently specified, we will assume Gaussian, uncorrelated and zero mean measurement noise throughout the paper (which is a common assumption and not directly affected by the separation between observations) such that the non-Gaussianity of the determined state will be only due to the effect of nonlinearities, which is the main focus of our work. The LS solver is implemented to make the most of differential algebra (DA) techniques (Berz 1986, 1987, 1999) and high-order terms are exploited to provide an accurate description of the confidence region. In particular, by using DA we can approximate the LS target function as an arbitrary-order polynomial, thus enabling a high-order representation of the confidence region. This accurate representation of the confidence region directly in IOD is of crucial importance for observation correlation and initialization of Bayesian estimators (Schumacher et al. 2015).

After finding the OD solution and its uncertainty region, in most practical applications it is necessary to draw samples according to OD statistics. These applications include initialization of particle filters (Simon 2006) and computation of collision probability (Jones et al. 2015). In this work, we propose four methods for the nonlinear representation of the LS confidence region. The first method is based on the concept of gradient extremal (GE) (Hoffman et al. 1986), which has already been introduced in astrodynamics under the name of line of variation (LOV) (Milani et al. 2005). Due to the effect of nonlinearities, the numerical procedure to determine samples on the LOV is quite complex for short arcs (Milani and Gronchi 2010). DA techniques are introduced here to simplify this numerical procedure by taking advantage of the polynomial representation of the involved quantities. The developed technique can then be applied along any eigenvector of the solution covariance matrix. In the second method, the concept of LOV is extended to cases in which the confidence region is shown to be two-dimensional, by introducing the gradient extremal surface (GES) The third approach combines a mono-dimensional LOV with its or a high-order DA polynomial to obtain a two-dimensional sampling. Finally, a method to enclose the confidence region in a six-dimensional box is introduced. This approach could be particularly useful for applications in which high accuracy is required, e.g., the computation of low collision probabilities. The proposed algorithms for solving the LS problem and the nonlinear representation of the confidence region are accompanied by the definition of indices to estimate the relevance of high-order terms and to determine the dimensionality of the confidence region.

The work presented in this paper is based on preliminary results shown in Principe et al. (2016, 2017). In representing the confidence region, new algorithms are presented taking advantage of, and extending, the concept of GE. The effectiveness of this approach is tested with even shorter arc lengths than in Principe et al. (2016). Furthermore, indices are introduced to establish the most suitable description of the confidence region.

The paper is organized as follows. First, a description of the LS method and the confidence region of the LS solution is given. The DA implementation of the LS solver is presented next, followed by some algorithms used to nonlinearly characterize and sample the confidence region. An introduction to the indices and our strategy for dealing with IOD problems on short arcs conclude this section. The properties and performance of the proposed approaches are assessed using a realistic observational scenario of four objects in different orbital regimes. Some final remarks conclude the paper.

2 Classical least squares

We need to find the solution of the OD problem in order to track RSOs. Thus, given some observations, the aim is to compute the orbit of an object. The orbit is expressed in terms of an n-dimensional state vector at a reference epoch ${\varvec{x}}(t_0)$. Different ways of expressing the state vector can be used, e.g., in the modified equinoctial elements (MEE) (Walker et al. 1985), or as a position-velocity vector $({\varvec{r}},{\varvec{v}})$ in the Earth-centered inertial (ECI) coordinates.

The OD problem is generally addressed by using the LS method, devised by Gauss (1809). Input of the algorithm is a tentative value ${\varvec{x}}={\varvec{x}}(t_0)$. Then, the predicted observations are computed at each observation epoch. Let ${\varvec{y}}$ be an m-dimensional vector containing the predicted observations, that is ${\varvec{y}}={\varvec{h}}({\varvec{x}})$, where m is the number of measurements. Note that ${\varvec{h}}$ is a nonlinear function that composes the propagation from the reference epoch to observation epochs with the observations space projection. The differences between the actual observations ${\varvec{y}}_\mathrm{{obs}}$ and the predicted ones ${\varvec{y}}$ are referred to as residuals. The residuals are collected in the m-dimensional vector ${\varvec{\xi }}={\varvec{y}}_\mathrm{{obs}}-{\varvec{y}}$. The LS solution is the state vector ${\varvec{x}}^*$ that minimizes the target function

$$\begin{aligned} J({\varvec{x}})={\varvec{\xi }}^T({\varvec{x}}){\varvec{\xi }}({\varvec{x}}). \end{aligned}$$

(1)

We can find the minimum of $J({\varvec{x}})$ by computing its stationary points, i.e.,

$$\begin{aligned} {\varvec{x}}^*:\frac{\partial J}{\partial {\varvec{x}}}({\varvec{x}}^*)={\varvec{0}}. \end{aligned}$$

(2)

It is worth noting that ${\varvec{x}}^*$ can be a minimum, maximum, as well as a saddle. Thus, to ensure that ${\varvec{x}}^*$ is a minimum, it is required that the Hessian of the target function in the stationary point, $H^* = \frac{\partial ^2 J}{\partial {\varvec{x}}^2}({\varvec{x}}^*)$, is positive definite.

To solve the system of nonlinear equations given by Eq. (2), we can use an iterative method, e.g., Newton’s method. Convergence of this method is ensured if a suitable initial estimate is available. This estimate is usually obtained by solving the IOD problem, in which the number of observations is minimum, $m = n$. The solution of the iterative method is (Milani and Gronchi 2010)

$$\begin{aligned} {\varvec{x}}_{i+1}={\varvec{x}}_i-C^{-1}F^T{\varvec{\xi }}, \end{aligned}$$

(3)

where ${\varvec{x}}_i$ is available from previous iterations or is the IOD solution when $i=1$. F is an m x n matrix with the partial derivatives of the residuals with respect to the state vector components, that is

$$\begin{aligned} F_{pq}=\frac{\partial \xi _p}{\partial x_q}({\varvec{x}}_i) \quad \hbox { for } p=1,\dots ,m \quad \text {and} \quad q=1,\dots ,n. \end{aligned}$$

(4)

C is the n x n normal matrix,

$$\begin{aligned} C=F^TF+{\varvec{\xi }}^T({\varvec{x}}_i)S, \end{aligned}$$

(5)

and S an m x n x n array with elements

$$\begin{aligned} S_{pqr}=\frac{\partial ^2\xi _p}{\partial x_q \partial x_r} \quad \hbox { for } p=1,\dots ,m \quad \text {and} \quad q,r=1,\dots ,n. \end{aligned}$$

(6)

The full Newton’s method is generally not used for OD problems, because of practical problems in the computation of the second derivatives in matrix S (Milani 1999). For this reason, the term ${\varvec{\xi }}^TS$ in Eq. (5) is often neglected. This quantity is negligible when the residuals are small. The resulting method is called the differential correction technique (Milani and Gronchi 2010) or Gauss–Newton method (Hansen et al. 2013).

2.1 Confidence region and statistical properties of the LS solution

The solution of the LS ${\varvec{x}}^*$, although minimizing the cost function, does not generally correspond to the true orbit, which lies within an uncertainty set around the LS solution, the so-called confidence region. From an optimization perspective, following Milani and Gronchi (2010), the confidence region includes orbits with acceptable target functions. To determine the confidence region, the target function $J({\varvec{x}})$ is expressed as

$$\begin{aligned} J({\varvec{x}})=J^*+\delta J({\varvec{x}}), \end{aligned}$$

(7)

where $J^*=J({\varvec{x}}^*)$ and $\delta J({\varvec{x}})$ is called the penalty. Then, the confidence region Z is defined as the region in which $\delta J$ is smaller than or equal to the control value $K^2$ (a method to determine $K^2$ is provided in Sect. 4). Thus,

$$\begin{aligned} Z(K)=\{{\varvec{x}}\in A \subseteq \mathbb {R}^n : \delta J({\varvec{x}})\le K^2 \}, \end{aligned}$$

(8)

where the subset A depends on the chosen orbital elements. The target function $J({\varvec{x}})$ is usually expanded around ${\varvec{x}}^*$ at second order, i.e., linearizing the mapping between the state and observation, resulting in

$$\begin{aligned} \begin{array}{lll} J({\varvec{x}})\approx & {} J^*+ \nabla J({\varvec{x}}-{\varvec{x}}^*)+\frac{1}{2}({\varvec{x}}-{\varvec{x}}^*)^TH({\varvec{x}}-{\varvec{x}}^*), \end{array} \end{aligned}$$

(9)

where $\nabla J = \frac{\partial J}{\partial {\varvec{x}}}({\varvec{x}}^*)$ and

$$\begin{aligned} H_{pq}=\frac{\partial ^2J}{\partial x_p \partial x_q} \quad p,q=1,\ldots ,n. \end{aligned}$$

(10)

The Hessian matrix H can be expressed as

$$\begin{aligned} H=2(F^TF+\xi ^T\xi )=2C. \end{aligned}$$

(11)

Reminding that $\frac{\partial J}{\partial {\varvec{x}}}({\varvec{x}}^*) = {\varvec{0}}$, the confidence region definition becomes

$$\begin{aligned} \delta J({\varvec{x}}) \approx ({\varvec{x}}-{\varvec{x}}^*)^TC({\varvec{x}}-{\varvec{x}}^*)\le K^2. \end{aligned}$$

(12)

This expression can be then manipulated by taking advantage of the eigen decomposition theorem:

$$\begin{aligned} C=VC_dV^{-1}=VC_dV^T. \end{aligned}$$

(13)

V is a square matrix, whose columns are the eigenvectors of C, while $C_d$ is a diagonal matrix containing eigenvalues of C (Franklin 1968).

Hence, the confidence region expression becomes

$$\begin{aligned} \delta J({\varvec{x}})=({\varvec{\tilde{x}}}- {\varvec{\tilde{x}}}^*)^TC_d ({\varvec{\tilde{x}}}- {\varvec{\tilde{x}}}^*)\le K^2, \end{aligned}$$

(14)

where

$$\begin{aligned} ({\varvec{\tilde{x}}}- {\varvec{\tilde{x}}}^*)=V^T({\varvec{x}}-{\varvec{x}}^*). \end{aligned}$$

(15)

Because C is positive definite, all of its eigenvalues are positive and $C_d$ can be expressed as

$$\begin{aligned} C_d=\begin{bmatrix} \frac{1}{\gamma _1^2}&\quad 0&\quad \dots&\quad 0 \\ \vdots&\quad \ddots&\quad&\quad \vdots \\ \vdots&\quad&\quad \ddots&\quad \vdots \\ 0&\quad \dots&\quad \dots&\quad \frac{1}{\gamma _n^2} \end{bmatrix}, \end{aligned}$$

(16)

where $\gamma _1^2,\ldots ,\gamma _n^2>0$. Then, Eq. (14) becomes

$$\begin{aligned} \sum _{i=1}^n \frac{({\tilde{x}}_i-{\tilde{x}}^*_i)^2}{\gamma _i^2}\le K^2. \end{aligned}$$

(17)

In conclusion, due to the quadratic form of the penalty, the confidence region is represented by an ellipsoid with axes aligned with the columns of V and size determined by

$$\begin{aligned} \tilde{x}_i = \tilde{x}^*_i \pm K \gamma _i, \text {with}\ i= 1,\dots ,n. \end{aligned}$$

(18)

The LS method can also be endowed with a probabilistic interpretation, in which its solution is a random vector due to the random nature of the measurements. If the mapping between state and residuals is linearized and the measurement noise is assumed to be randomly distributed, uncorrelated, and with zero mean value, then the first two statistical moments of the solution can be straightforwardly derived from those of the measurements. Specifically, ${\varvec{x}}^*$ is the solution mean and the covariance matrix is given by the inverse of the normal matrix $P=C^{-1}$ (Montenbruck and Gill 2000). Moreover, with the additional assumption of Gaussian noise, the LS solution is distributed according to a multivariate Gaussian probability density function (PDF) $p({\varvec{x}})$ (Gauss 1809), and the first two statistical moments fully statistically describe the solution. Then,

$$\begin{aligned} p({\varvec{x}}) = \frac{1}{\sqrt{(2\pi )^{n}|P|}}e^{-\frac{1}{2}({\varvec{x}}-{\varvec{x}}^*)^TP^{-1}({\varvec{x}}-{\varvec{x}}^*)}, \end{aligned}$$

(19)

where |P| is the determinant of P. In this case, contour levels of $\delta J({\varvec{x}})$ are also contour levels of $p({\varvec{x}})$, thus ellipsoids with equal residual values (boundaries of the confidence region) are surfaces of equal probability.

3 Least squares solution with differential algebra

DA techniques enable the efficient computation of derivatives of functions within a computer environment. The unfamiliar reader can refer to Berz (1999) for theoretical aspects and to Armellin et al. (2010) for a self-contained introduction for applications in astrodynamics. Here we take advantage of DA techniques to develop a high-order iterative algorithm to solve LS problems. We first describe a general procedure that finds the solution of a system of nonlinear equations, ${\varvec{g}}({\varvec{x}})={\varvec{0}}$, in the DA framework. This algorithm was presented in Principe et al. (2016) and is recalled here for the sake of clarity. The algorithm is as follows:

• 1. Given the solution ${\varvec{x}}_i$ (from the previous iteration, or from the initial guess when $i=1$), initialize the state vector ${\varvec{x}}_i$ as a kth-order DA vector and evaluate the function ${\varvec{g}}$ in the DA framework, thus obtaining the kth-order Taylor expansion of ${\varvec{g}}$, $\mathcal {T}_{{\varvec{g}}}^k$:

  $$\begin{aligned} {\varvec{g}}\approx \mathcal {T}_{{\varvec{g}}}^k({\varvec{x}}_i). \end{aligned}$$

  (20)

• 2. Invert the map (20) to obtain

  $$\begin{aligned} {\varvec{x}}_i \approx \mathcal {T}_{{\varvec{x}}_i}^k({\varvec{g}}). \end{aligned}$$

  (21)

• 3. Evaluate $\mathcal {T}_{{\varvec{x}}_i}^k({\varvec{g}})$ at ${\varvec{g}} = {\varvec{0}}$ to compute the updated solution as

  

  (22)

• 4. Repeat (1)–(3) until a convergence criterion is met or the maximum number of iterations is reached.

After convergence, the algorithm supplies ${\varvec{x}}^*$, the solution of the system ${\varvec{g}}({\varvec{x}})={\varvec{0}}$, as well as the high-order Taylor expansion of the function ${\varvec{g}}$ around ${\varvec{x}}^*$, $\mathcal {T}_{{\varvec{g}}}^k({\varvec{x}}^*)$. When solving the LS problem, we need to find the stationary point of the target function $J({\varvec{x}})$. Thus, we need to solve the system of nonlinear equations $\frac{\partial J}{\partial {\varvec{x}}}({\varvec{x}})=0$. We can hence set ${\varvec{g}}({\varvec{x}})=\frac{\partial J}{\partial {\varvec{x}}}({\varvec{x}})$ in the algorithm and obtain an arbitrary-order solver of the LS problem. It will be referred to as the differential algebra least squares (DALS) solver.

The DALS solver’s main advantage is its polynomial approximation of the objective function $J({\varvec{x}})$. Thus, we can take advantage of the analytical expression of $J({\varvec{x}})$ in the neighborhood of a minimum and analyze the nonlinear description of the confidence region. In addition, as the objective function $J({\varvec{x}})$ is expanded up to an arbitrary order, the correct (full) expression of the Hessian matrix H is available. We can then check whether $H({\varvec{x}}^*)$ is positive definite, i.e., ${\varvec{x}}^*$ is actually a minimum. This feature is not a natural part of the differential correction algorithm, as the full expression of H is not available. However, the algorithm can be extended and the Hessian computed in order to categorize ${\varvec{x}}^*$.

We implemented two convergence criteria: one based on the correction size, one based on the target function variation. Thus, the iterative process is halted when at least one of the two following requirements is met:

$$\begin{aligned}&||{\varvec{x}}_{i+1}-{\varvec{x}}_{i} ||_\infty \le \epsilon _x,\nonumber \\&\left| J_{i+1}-J_{i}\right| \le \epsilon _J, \end{aligned}$$

(23)

where $\epsilon _x$ and $\epsilon _J$ are established tolerances.

In this section, we presented an algorithm that can work at arbitrary order. However, including terms above the second order did not improve the convergence rate of the algorithm while significantly enlarged the execution time. Thus, a second-order DALS solver is used in this work. Note that, in order to exploit high-order terms, it would be necessary to use step-size control mechanisms, which have not been implemented yet.

After convergence of the second-order DALS solver, a kth-order Taylor expansion of $J({\varvec{x}})$ around the optimal solution can be computed.

4 Confidence region representation

When we deal with short observational arcs, nonlinearities in the mapping between observations and state are relevant. Thus, we need to take into account terms above 2nd-order in the expression of $J({\varvec{x}})$. Due to the non-negligible high-order terms, even when the measurement noise is assumed to be Gaussian, the solution statistics are no longer guaranteed to be Gaussian and surfaces of equal probability are no longer guaranteed to be ellipsoids. In this section we show some algorithms to accurately describe the confidence region of the LS solution. For this purpose, we take advantage of the high-order representation of the target function $J({\varvec{x}})$ supplied by the DALS. Such algorithms are essential in many applications, e.g., to draw samples when correlating observations or to initialize a particle filter (Simon 2006).

The algorithm exploits the kth-order Taylor expansion of $J({\varvec{x}})$ around the optimal solution provided by DALS after convergence

$$\begin{aligned} J({\varvec{x}}) = J^* + \delta J({\varvec{x}}) \approx J^*+ \mathcal {T}_{\delta J}^k({\varvec{x}}), \end{aligned}$$

(24)

where ${\varvec{x}} ={\varvec{x}}^* + \delta {\varvec{x}}$. In Eq. (24), terms up to order k are retained.

The F-test method (Seber and Wild 2003) can be used, with the assumption of Gaussian measurement noise, to determine the value of the control parameter $K^2$, introduced in Eq. (8), corresponding to the desired confidence level even when high-order terms are retained in the representation of the penalty. For a confidence level of $100(1-\alpha )\%$, we have

$$\begin{aligned} \mathcal {T}_{\delta J}^k({\varvec{x}})\le \frac{n}{m-n}J^*F^{\alpha }_{n,m-n}=K^2, \end{aligned}$$

(25)

in which $F^{\alpha }_{n,m-n}$ is the upper $\alpha$ percentage point of the F-distribution.

4.1 Line of variation

The LS confidence region is in general described as an n-dimensional region. However, this region is sometimes stretched along one direction, which is called the weak direction and defined as the predominant direction of uncertainty in an orbit determination problem (Milani et al. 2005). In other words, the weak direction is the direction along which the penalty $\delta J$ is less sensitive to state vector variations.

The confidence region is an ellipsoid if the purely quadratic terms are retained in the expression of $\delta J$. Thus, sampling along the weak direction consists in sampling the semi-major axis of the ellipsoid. However, the second-order approximation may not be accurate enough to properly represent the target function. When high-order terms are retained in the expression of J, the weak direction is point dependent (i.e., we can define a local weak direction) and the resulting curve may not be a straight line. Even a very small deviation from the above-mentioned curve causes the target function to quickly increase. Thus, due to the steepness of J, the sampling process along the weak direction is not straightforward.

The graph of the function J can be thought of as a very steep valley with an almost flat river at the bottom (Milani and Gronchi 2010). Thus, when the confidence region is stretched along one direction, samples can be obtained by looking for points on the valley floor. The valley floor of a function is the line that connects points on different contour subspaces for which the gradient’s absolute value is minimum. This locus of points is called a function’s GE (Hoffman et al. 1986). A GE intersects every contour line where the gradient is smallest in absolute value compared to other gradient values on the same contour (Hoffman et al. 1986). The concept of GE was already used in astrodynamics to perform a mono-dimensional sampling of the LS confidence region, and it is known as LOV (Milani et al. 2005).

Let $C_S$ be the contour subspace, that is the nonlinear subspace defined by contour lines of $J({\varvec{x}})$, where $J({\varvec{x}})=\text {const}$. Note that at every point ${\varvec{x}}_{GE}$ on $C_S$ the gradient is perpendicular to $C_S$. For a point ${\varvec{x}}_{GE}$ to belong to the valley floor, the norm of the target function’s gradient $|\nabla J |$ needs to be extremal, and therefore

$$\begin{aligned} {\varvec{x}}_{GE}=\{{\varvec{x}} \in C_S : \nabla J({\varvec{x}})=\min _{{\varvec{x}} \in C_S}{|\nabla J({\varvec{x}}) |}=\min _{{\varvec{x}} \in C_S}{ \nabla J({\varvec{x}})^2 }\}. \end{aligned}$$

(26)

Let $R({\varvec{x}})$ be the projecting matrix onto the space tangent to $C_S$ at ${\varvec{x}}$ and $R^0({\varvec{x}})$ be the projecting matrix in the direction of $\nabla J$. Equation (26) can be written as

$$\begin{aligned} {\varvec{x}}_{GE}=\{{\varvec{x}}\in C_S:R({\varvec{x}})\nabla (\nabla J)^2={\varvec{0}}\}, \end{aligned}$$

(27)

in which we omitted the dependency of J on ${\varvec{x}}$ to simplify the notation. The quantity $\nabla (\nabla J)^2$ can be expressed as

$$\begin{aligned} \nabla (\nabla J)^2=2H\nabla J, \end{aligned}$$

(28)

that is the product of the Hessian and the gradient of J. This quantity can then be decomposed in a projection parallel to $\nabla J$,

$$\begin{aligned} R^0H\nabla J=\lambda \nabla J, \end{aligned}$$

(29)

and a projection perpendicular to $\nabla J$,

$$\begin{aligned} RH\nabla J=H\nabla J-\lambda \nabla J. \end{aligned}$$

(30)

Thus, the condition in Eq. (27) becomes

$$\begin{aligned} H\nabla J=\lambda \nabla J. \end{aligned}$$

(31)

Equation (31) must hold for every point on a GE. Thus, a GE is a locus of points where the gradient of $J({\varvec{x}})$ is an eigenvector of the Hessian of $J({\varvec{x}})$, a one-dimensional curve in an n-dimensional space  (Hoffman et al. 1986). Let ${\varvec{v}}_i$ be an eigenvector of H and ${\varvec{g}}=\nabla J$, then the necessary and sufficient condition for a point to belong to the GE can be rewritten as

$$\begin{aligned} {\varvec{g}}^T{\varvec{v}}_j=0 \quad \hbox { for } j=1,\dots ,n; \quad j\ne i. \end{aligned}$$

(32)

Equation (32) is a system of $(n-1)$ conditions that define a one-dimensional curve and it is apparent that there are n different curves, corresponding to the n different eigenvectors of the Hessian matrix. In the literature, the LOV is typically the GE corresponding to ${\varvec{v}}_1$, the eigenvector associated with the minimum eigenvalue of the Hessian matrix. This direction identifies the weak direction of the OD problem. It is worth remarking that n LOVs can be computed, one for each of the n eigenvectors of the Hessian matrix. However, as the length of the LOV is shorter for the eigenvectors associated with higher eigenvalues, nonlinearities are likely to be significant only in the computation of the first LOVs.

The LOV definition can be generalized to $m\le n$ dimensions by allowing i in Eq. (32) to take m values. These conditions define an m-dimensional surface where gradient ${\varvec{g}}$ at each point lies in the linear subspace spanned by m eigenvectors of the Hessian H. It is apparent that each $\mathbf{LOV}_i$ lies totally on a higher-dimensional surface. As already explained in Milani et al. (2004), the uncertainty region with short arcs tends to a bi-dimensional set. Thus, in these cases we can extend the LOV concept to the GE surface identified by ${\varvec{v}}_1$ and ${\varvec{v}}_2$, the two eigenvectors associated with the two smallest eigenvalues of H. We will refer to this surface as the GES.

4.1.1 Line of variation algorithm

We propose an algorithm to compute the LOV (along an arbitrary eigenvector), taking advantage of DA tools. The algorithm assumes that the DALS solver has been used to obtain the reference solution ${\varvec{x}}_i={\varvec{x}}^*$ of the LS problem and the kth-order Taylor approximation of $\delta J$, $\mathcal {T}_{\delta J}^k({\varvec{x}})$. Thus, the algorithm proceeds as follows:

• 1. Let $K\gamma _1$ be the length of the second-order ellipsoid along the eigenvector ${\varvec{v}}_1({\varvec{x}}^*)$ as shown in Eq. (18), and $\varDelta x=\frac{K\gamma _1}{h}$ with h depending on the desired sampling rate.

• 2. Extract from $\mathcal {T}_{\delta J}^k({\varvec{x}}_i)$ the Taylor approximation of the Hessian $\mathcal {T}^k_H({\varvec{x}}_i)$ of J and calculate its eigenvectors and eigenvalues at ${\varvec{x}}_i$. Compute the point ${\varvec{x}}{\prime }_{i+1}={\varvec{x}}_i \pm \varDelta x\,{\varvec{v}}_1$, in which ${\varvec{v}}_1({\varvec{x}}_i)$ is the eigenvector corresponding to the minimum eigenvalue.

• 3. Let $L({\varvec{x}}{\prime }_{i+1})$ be the hyperplane spanned by the eigenvectors ${\varvec{v}}_j({\varvec{x}}{\prime }_{i+1})$ with $j=2,\dots 6$ and passing through ${\varvec{x}}{\prime }_{i+1}$, i.e.,

  $$\begin{aligned} L({\varvec{x}}{\prime }_{i+1})=\{{\varvec{y}}|\quad ({\varvec{y}}-{\varvec{x}}{\prime }_{i+1})\cdot {\varvec{v}}_1({\varvec{x}}{\prime }_{i+1})=0\}. \end{aligned}$$

  (33)

  Compute the point ${\varvec{x}}_{i+1}$, belonging to $L({\varvec{x}}{\prime }_{i+1})$ and such that ${\varvec{\nabla }} J({\varvec{x}}_{i+1})\parallel {\varvec{v}}_1({\varvec{x}}_{i+1})$. This is equivalent to finding the solution of the system

  $$\begin{aligned} \left\{ \begin{array}{l} ({\varvec{x}}_{i+1}-{\varvec{x}}{\prime }_{i+1})\cdot {\varvec{v}}_1({\varvec{x}}_{i+1})=0\\ \nabla J({\varvec{x}}_{i+1})\cdot {\varvec{v}}_j({\varvec{x}}_{i+1})=0 \quad j=2,\dots ,6. \end{array} \right. \end{aligned}$$

  (34)

• 4. Repeat steps (2)–(3), until the value of $\delta J({\varvec{x}}_{i+1}) \approx \mathcal {T}_{\delta J}^k({\varvec{x}}_{i+1}) \le K^2$, i.e., the boundary of the confidence region is reached.

The output is a set of points ${\varvec{x}}_i^{LOV}$, with $i=1,\ldots ,l$ that describe the LOV. It is worth mentioning that the approximation $\mathcal {T}_{\delta J}^k$, initially provided by the DALS solver, is recomputed whenever a point of the LOV falls outside the region where the truncation error of the polynomial approximation is acceptable. The estimated truncation error is computed using the approach described in Wittig et al. (2015). Although the algorithm presented here describes the computation of the $\mathbf{LOV}_1$, i.e., the GE along ${\varvec{v}}_1$, it can be run along any eigenvector direction, thus providing up to six LOVs.

4.2 Gradient extremal surface algorithm

When the confidence region is not accurately described by one LOV, it is often sufficient to adopt a 2-D description of the region. This region can be represented by the GES defined by ${\varvec{v}}_1$ and ${\varvec{v}}_2$ (the two eigenvectors associated to the smallest eigenvalues of H). This surface has the property that, at each of its points, the gradient of J lies on the plane spanned by ${\varvec{v}}_1$ and ${\varvec{v}}_2$. The following algorithm is proposed to compute the points belonging to this surface:

• 1. Run the algorithm described in Sect. 4.1.1. The resulting set of l points is referred to as ${\varvec{x}}^{{LOV}_1}$.

• 2. Take a point of ${\varvec{x}}^{{LOV}_1}$ as initial point, ${\varvec{x}}_{i,0} ={\varvec{x}}_i^{{LOV}_1}$.

• 3. Compute ${\varvec{x}}{\prime }_{i,k+1}={\varvec{x}}_{i,k}\pm \varDelta x\,{\varvec{v}}_2$, in which $\varDelta x$ is a chosen length as in 4.1.1.

• 4. Let $L({\varvec{x}}{\prime }_{i,k+1})$ be the hyperplane spanned by the eigenvectors ${\varvec{v}}_j({\varvec{x}}{\prime }_{i,k+1})$ with $j=3,\dots 6$ and passing through ${\varvec{x}}{\prime }_{i,k+1}$. Compute the point ${\varvec{x}}_{i,k+1}$, which belongs to $L({\varvec{x}}{\prime }_{i,k+1})$ and such that ${\varvec{\nabla }} J({\varvec{x}}_{i,k+1})$ is orthogonal to it. This is equivalent to finding the solution of the system

  $$\begin{aligned} \left\{ \begin{array}{l} ({\varvec{x}}_{i,k+1}-{\varvec{x}}{\prime }_{i,k+1})\cdot {\varvec{v}}_1({\varvec{x}}_{i,k+1})=0\\ ({\varvec{x}}_{i,k+1}-{\varvec{x}}{\prime }_{i,k+1})\cdot {\varvec{v}}_2({\varvec{x}}_{i,k+1})=0\\ \nabla J({\varvec{x}}_{i,k+1})\cdot {\varvec{v}}_j({\varvec{x}}_{i,k+1})=0 \quad j=3,\dots ,6. \end{array} \right. \end{aligned}$$

  (35)

• 4. Repeat steps (3)–(4), until the value of $\delta J({\varvec{x}}_{i,k+1}) \approx \mathcal {T}_{\delta J}^k({\varvec{x}}_{i,k+1}) \le K^2$, i.e., the boundary of the confidence region is reached.

• 5. Repeat the steps (2)–(5) for all points ${\varvec{x}}_{i,0} ={\varvec{x}}_i^{{LOV}_1}$, $i=1,\ldots ,l$.

This algorithm allows us to obtain a two-dimensional description of the confidence region, even when $\mathbf{LOV}_2$ is not a straight line. However, this procedure is computationally intensive as the set of nonlinear equations Eq. (35) need to be solved for every point on the surface. However, it is worth noting that Eq. (35) is a set of polynomial equations (as we are working with Taylor approximations), and this makes the algorithm viable from a computational time standpoint. Moreover, when $\mathbf{LOV}_2$ approximates a straight line, the more efficient algorithm in Sect. 4.3 can be used to sample the uncertainty region.

4.3 Arbitrary direction sampling

When nonlinearities are significant only along the weak direction but the confidence region cannot be represented as a one-dimensional curve, a simplified version of the algorithm described in Sect. 4.2 can be adopted. This algorithm will be referred to as the arbitrary direction (AD) algorithm and is summarized as follows:

• 1. Run the algorithm described in Sect. 4.1.1. The resulting set of l points is referred to as ${\varvec{x}}^{LOV}$.

• 2. Take one point from ${\varvec{x}}^{LOV}$ as initial point, ${\varvec{x}}_{i,0} ={\varvec{x}}_i^{LOV}$.

• 3. Select a direction ${\varvec{v}}$ in the state vector space along which we want to sample the confidence region. This direction can be ${\varvec{v}}_2$ (i.e., the eigenvector corresponding to the second smallest eigenvalue of H) or any other direction of interest, including a random one.

• 4. Generate a set of samples ${\varvec{x}}_{i,k+1} = {\varvec{x}}_{i,k} \pm \varDelta x {\varvec{v}}$ in which $\varDelta x$ is a fraction of $K\gamma _i$ along ${\varvec{v}}$. Stop when $J({\varvec{x}}_{i,k+1}) \ge J({\varvec{x}}^*)+K^2$.

• 5. Repeat steps (3)–(4) for the desired number of directions.

• 6. Repeat steps (2)–(5) for all points ${\varvec{x}}_i^{LOV}$ with $i=1,..,l$.

This algorithm avoids solving the system of nonlinear equations (35). However, it can be applied to accurately sample the confidence region only when the curvature along the selected directions is negligible. In addition, by generating a set of random directions, the algorithm can be used to produce samples at the confidence region boundaries for different confidence levels.

4.4 Full enclosure of the confidence region with ADS

The LOV is a one-dimensional representation of the LS confidence region. When this is not a good approximation, the GES approach enables a bi-dimensional representation. In some cases (e.g., for the computation of low collision probabilities or the initialization of particle filters in state estimation), it may be necessary to consider a full n-dimensional representation of the confidence region. We can apply automatic domain splitting (ADS) techniques (Wittig et al. 2015) to enclosure this region with a set of boxes on which the penalty function is accurately represented by multiple Taylor polynomials. These boxes can be obtained using the following steps:

• 1. Let $H({\varvec{x}}^*)$ be the Hessian of the target function evaluated at ${\varvec{x}}^*$. Compute the eigenvectors of $H({\varvec{x}}^*)$ and store them column-wise in the matrix V.

• 2. Compute an n-th dimensional box enclosure of the LS confidence region. This is achieved by determining the box D that encloses both the second-order confidence region expressed by Eq. (18), and (when necessary, see Sects. 4–5 for details) the $\mathbf{LOV}_j$ expressed in the eigenvector space. This last set of points is obtained by multiplying the $\mathbf{LOV}_j$ points by $V^{T}$:

  $$\begin{aligned} \tilde{{\varvec{x}}}_i^{{LOV}_j}=V^T{\varvec{x}}_i^{{LOV}_j}, \quad \hbox { for } i=1,\dots ,l \quad \text {and} \quad j=1,\dots ,n. \end{aligned}$$

  (36)

• 3. Compute the high-order expansion of the penalty in the eigenvector space, $\mathcal {T}^k_{\delta J_V}(\tilde{{\varvec{x}}})$, with $\tilde{{\varvec{x}}}=V^T{\varvec{x}}$.

• 4. Apply ADS to the Taylor expansion $\mathcal {T}^k_{\delta J_V}(\tilde{{\varvec{x}}})$ over the domain D to ensure that the truncation error is below a given threshold on D. As a result, D is split into a set of subdomains and a corresponding set of Taylor approximations of $\delta J_V(\delta \tilde{{\varvec{x}}})$ are computed.

• 5. Find the minimum of $\mathcal {T}^k_{\delta J_V}(\delta \tilde{{\varvec{x}}})$ over each subdomain and retain only the subdomains in which the minimum is smaller than $J({\varvec{x}}^*)+K^2$. This step is obtained by running an optimizer (e.g., MATLAB fmincon function) on each local Taylor polynomial.

The result of the algorithm is a set of subdomains that cover the nonlinear LS confidence region. Note that, as D encloses both the $\mathbf{LOV}_j$ and the second-order confidence region, it will likely enclose the full nonlinear confidence region. In addition, it is worth mentioning that D is defined in the eigenvector space to reduce the wrapping effect. Once we have enclosed the uncertainty domain in the box D and computed the accurate polynomial representation of the penalty in this domain, we can introduce the high-order extension of the solution pdf, $p^k({\varvec{x}})$. By analogy with the Gaussian representation introduced at the end of Sect. 2.1, we make the assumption that $p^k({\varvec{x}})$ can be expressed as:

$$\begin{aligned} p^k({\varvec{x}})=\frac{1}{\int _D e^{-\frac{1}{2}\mathcal {T}^{k}_{\delta J} ({\varvec{x}})}\text {d} {\varvec{x}}}e^{-\frac{1}{2}\mathcal {T}^{k}_{\delta J} ({\varvec{x}})}. \end{aligned}$$

(37)

Although not rigorously the pdf of ${\varvec{x}}$, our assumption is motivated by the fact that, in this way, surfaces of equal residuals (nonlinear confidence region boundaries) remain surfaces of equal probability and that Eq. (37) returns the normal distribution $p({\varvec{x}})$ of Eq. (19) when the high-order terms in $J({\varvec{x}})$ are negligible. The integral, introduced to normalize the pdf to 1 over D, is evaluated by means of Monte Carlo integration:

$$\begin{aligned} \int _D e^{-\frac{1}{2}\mathcal {T}^{k}_{\delta J} ({\varvec{x}})}\text {d} {\varvec{x}}\approx \frac{1}{N} \sum _i\frac{e^{-\frac{1}{2}\mathcal {T}^{k}_{\delta J} ({\varvec{x}}_i)}}{q({\varvec{x}}_i)}, \end{aligned}$$

(38)

where N is the number of samples generated according to the importance sampling distribution $q({\varvec{x}})$. The normal multivariate distribution $p({\varvec{x}})$ defined in Eq. (19) is selected as the importance sampling distribution to speed up the Monte Carlo integration convergence rate. Note that the integral in Eq. (38) could be approximated using DA integration tools. However, this would require the Taylor expansion of $e^{-\frac{1}{2}\mathcal {T}^{k}_{\delta J}({\varvec{x}})}$, which would generate a large number of subdomains for an accurate representation.

5 Strategy for confidence region representation

OD problems do not always need high-order methods to describe the confidence region. Similarly, the description of the confidence region does not always require an n-th dimensional representation. In this section, we first introduce some indices to capture the main features of the uncertainty region and then we describe our strategy to describe it balancing computational effort and accuracy.

5.1 High-order index

After computing the DALS solution and the polynomial approximation of J, we want to define an index to assess the relevance of high-order terms. Recalling Eqs. (19) and (37), we define the index

$$\begin{aligned} \varGamma _H = \dfrac{\int _{-\infty }^{\infty }\left| e^{-\frac{1}{2}\mathcal {T}^{k}_{\delta J} ({\varvec{x}})}-e^{-\frac{1}{2}\mathcal {T}^{2}_{\delta J} ({\varvec{x}})}\right| \text {d} {\varvec{x}}}{\int _{- \infty }^{\infty } e^{-\frac{1}{2}\mathcal {T}^{2}_{\delta J} ({\varvec{x}})} \text {d} {\varvec{x}}}. \end{aligned}$$

(39)

This index quantifies the effect of nonlinearities by measuring how much the statistics of LS solution deviate from Gaussianity when high-order terms are retained in the penalty expression. The integral in the denominator in Eq. (39) is $\sqrt{(2\pi )^{n}|P|}$, whereas the integral in the numerator is computed via a Monte Carlo method by generating a cloud of N samples distributed according to the second-order representation of J, i.e., according to $p({\varvec{x}}) = \mathcal {N}({\varvec{x}}^*,P)$. After some manipulation, the index can be approximated as

$$\begin{aligned} \varGamma _H \approx \frac{1}{N} \sum _i^N \left| e^{-\frac{1}{2}\left( \mathcal {T}^{k}_{\delta J} ({\varvec{x}}_i) - \mathcal {T}^{2}_{\delta J} ({\varvec{x}}_i)\right) } - 1 \right| . \end{aligned}$$

(40)

$\varGamma _H$ indicates whether high-order terms in J provide significant contribution over the entire uncertainty domain. This check is relevant, for instance, when we sample the solution pdf in the initialization of a particle filter. When the index shows that high-order terms are not relevant, we rely on a second-order representation of the LS confidence region. Otherwise, high-order analyses are performed starting with the computation of the LOV along the ${\varvec{v}}_1$ direction. Thus, to avoid wasting computational time on cases for which high-order terms are not relevant, the index is computed for $k=3$.

5.2 LOV index

When high-order terms turn out to be relevant, we might need to compute the LOVs associated with different eigenvectors to correctly represent the confidence region’s structure. However, high-order terms might only be relevant along certain directions. In particular, after sorting the covariance eigenvalues in decreasing order, if the high-order terms are neglected for specific eigenvectors, then they can be neglected for all subsequent ones.

Due to high-order terms, the LOVs may depart significantly from the second-order confidence ellipsoid axes. In particular, the LOVs could be stretched and/or curved. An index to assess the effect of nonlinearities on the LOV computation, $\varGamma _{LOV}$, can be defined as the relative error between the second-order and the kth-order representation of the pdf evaluated at the LOV points:

$$\begin{aligned} \varGamma _{LOV}=\frac{\sum _i \left| e^{-\frac{1}{2}\mathcal {T}^{k}_{\delta J} \left( {\varvec{x}}_i^{LOV}\right) }- e^{-\frac{1}{2}\mathcal {T}^{2}_{\delta J} \left( {\varvec{x}}_i^{LOV}\right) }\right| }{\sum _i e^{-\frac{1}{2}\mathcal {T}^{k}_{\delta J} \left( {\varvec{x}}_i^{LOV}\right) }}. \end{aligned}$$

(41)

$\varGamma _{LOV}$ can be used to assess how much the LOV departs from the confidence ellipsoid axis: the larger $\varGamma _{LOV}$, the more relevant the curvature and/or stretching is. As mentioned earlier, this index is first computed for the $\mathbf{LOV}_1$, i.e., along ${\varvec{v}}_1$. The $\mathbf{LOV}_2$ and its index are only computed when the result for $\mathbf{LOV}_1$ shows significant stretching or curvature. The procedure is halted when the index computed for a given LOV shows negligible effects from higher-order terms.

In the LOV algorithm, the polynomial expression of the target function J is recomputed when necessary. The need for recomputing can be quantified by substituting both the second-order and kth-order approximations of J in Eq. (41) without recomputing the polynomial.

5.3 Dimensionality index

The full representation of the confidence region requires generating samples that accurately describe the n-th dimensional confidence region. It is apparent that a huge number of samples may be required for a six-dimensional confidence region. To alleviate this problem, it is important to understand when a lower-dimensional sampling is sufficient (Milani et al. 2004). However, determining the dimensionality is not a trivial task as it strongly depends on the problem at hand, the coordinate representation, and the units and scaling factors adopted.

Here, an index is introduced based on the fact that a variation of an orbit’s semi-major axis causes its uncertainty region to quickly stretch along the orbit, making follow-up observations challenging. For this reason, we look at the impact the uncertainty along the different eigenvectors or LOVs has on the orbit semi-major axis. In particular, the index is defined as the variation of the mean anomaly M after one orbital period T due to the variation of the orbit’s semi-major axis associated with the ith direction, $\varDelta a_i$:

$$\begin{aligned} \varGamma _D^i= & {} \left| \dfrac{180}{\pi }\varDelta M^i \right| \approx \dfrac{180}{\pi }\left| \dfrac{\partial n^*}{\partial a}\right| \varDelta a^i T^*\nonumber \\= & {} \dfrac{3}{2} \dfrac{180}{\pi } \dfrac{n^*}{a^*} \varDelta a^i \dfrac{2\pi }{n^*} = 540 \dfrac{\varDelta a^i}{a^*}\ \ \text {[deg]}, \end{aligned}$$

(42)

in which n is the mean motion, and the starred quantities indicate properties of the LS solution. For example, an index value above one corresponds to a stretching of the uncertainty region of more than one degree after one orbital revolution along the LS solution orbit.

5.4 Summary of the algorithm

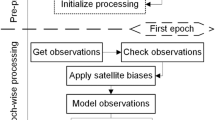
In Fig. 1, a summary of the proposed algorithm is shown:

• 1. Collect the observations (spread over a short arc).

• 2. Run the IOD and DALS solvers using all the observations acquired. As a result, the LS solution and the polynomial approximation of the target function are obtained.

• 3. Compute the index $\varGamma _H$. If $\varGamma _H$ is smaller than a given threshold, the second-order description of the confidence region is adopted. Else, a high-order analysis is carried out.

• 4. Start from $i=1$ and compute the $\mathbf{LOV}_i$ until $\varGamma _{LOV_{i}}$ is smaller than an established threshold.

• 5. Sample the region using one of the proposed algorithms.

Fig. 1

Flowchart of the proposed algorithm

6 Simulation results

For all the following test cases, optical observations (i.e., right ascension and declination) were simulated from Teide observatory, Tenerife, Canary Islands, Spain (observation code 954). Four different orbits were used as test cases: a low Earth orbit (LEO) (NORAD Catalog number 04784), a geostationary Earth orbit (GEO) (NORAD Catalog number 26824), a geostationary transfer orbit (GTO) (NORAD Catalog number 25542), and a Molniya orbit (NORAD Catalog number 40296). In  Principe et al. (2016), the same objects in LEO, GEO and Molniya were considered. However, in this work all algorithms were tested with shorter observational arcs. This section is divided in two parts: in the first one we analyze the convergence properties of the DALS algorithm, whereas in the second one we apply the strategy described in Sects. 4–5 to characterize the uncertainty region of the LS solution.

6.1 DALS convergence properties

The observation strategy adopted for GEO, GTO and Molniya objects involves re-observing the same portion of sky every 40 s, which is compatible with Siminski et al. (2014) and Fujimoto et al. (2014). The measurement noise is Gaussian with zero mean and standard deviation $\sigma =0.5$ arcsec. The object in LEO is assumed to be observed with a wide field-of-view camera, which takes observations every 5 s and has an exposure time of 3 s. In this case, $\sigma =5$ arcsec. In both cases, two scenarios with 8 or 15 observations are reproduced. In the 8-observation scenario, the arc length of the observation ranged from ${1.09}^{\circ }$ for the Molniya orbit to ${3.95}^{\circ }$ for the GTO; in the 15-observation scenario, the arc length ranged from ${2.14}^{\circ }$ for the Molniya orbit to ${7.44}^{\circ }$ for the GTO. In Table 1, the observation conditions are summarized.

Table 1 Test cases, observation window

The results discussed in this section assume the availability of an initial orbit, obtained by solving an IOD problem. In the computation of this preliminary solution, a high-order algorithm that solves two Lambert’s problems between the central epoch and the two ends of the observed arc is used. For more details, the reader can refer to Armellin et al. (2016). It is finally worth noting that Kepler’s dynamics are considered throughout this section, even though the proposed approach does not rely on any Keplerian assumption.

For each test case shown in Table 1, synthetic observations were generated by adding Gaussian noise to ideal observations and 100 simulations were run. The DALS solver estimated the orbit at the center of the observation window (at observation $\#4$ for the 8-observation scenario and $\#7$ for the 15-observation one). This approach proved to optimize both the algorithm performance and robustness. The tolerances $\epsilon _x$ and $\epsilon _J$ were such that convergence was reached when at least one of the following conditions was met:

$$\begin{aligned} ||\varDelta {\varvec{x}} ||_{\infty }\le \left\{ \begin{array}{c} \qquad 1\ \text {m} \quad \text {for position}, \\ 1\ \text {mm/s} \quad \text{ for } \text{ velocity }\end{array}\right. \qquad \varDelta J \le m \left( \frac{\sigma }{100}\right) ^2, \end{aligned}$$

where m is the number of measurements and $\sigma$ the standard deviation of the sensor noise.

The DALS solver always converged with LEO, GTO and Molniya orbits, while with GEO the convergence rate was $92\%$. The solver took on average 6 iterations. Thus, the observation arcs were long enough to guarantee a good convergence rate for the DALS solver. Note that the convergence of the algorithm does not provide any information on the quality of the solution. In Table 2, the median absolute error with respect to the reference orbit in position (km) and velocity (m/s) is reported for all test cases and scenarios. The estimation errors of the DALS solution were generally lower than those of the IOD solution, proving that including all the observations can improve the orbit estimation even for short arcs. In addition, the enhancement in accuracy granted by the LS was greater for longer observational arcs. For shorter observation arcs (8 observations), the median error was up to thousands kilometers, which hardens the task of performing follow-up observations. As expected, orbit estimation is more accurate for longer observation arcs, as the median error decreased with the number of observations.

Table 2 Median absolute value of the error (with respect to the true solution) in position (km) and velocity (m/s), for IOD and DALS solutions

As the true solution is supposed to be unknown in a real-world scenario, the solution accuracy was assessed by analyzing the absolute values of the residuals scaled by the measurements $\sigma$. The maximum median of absolute values was found for each test case among the 100 simulations and reported in Table 3. These values are compatible with the measurement statistics.

Table 3 Maximum median of the absolute value normalized residuals

Figure 2 reports the results of simulations for an 8-observation Molniya orbit scenario. The statistics of the absolute value normalized residuals are plotted and compared against the IOD solutions. The residuals of the IOD solutions vanished at observations #1,4,8, i.e., the observations used for the IOD solver. This is down to the fact that IOD solutions are deterministic and exactly reproduce the observations adopted for IOD. However, the residuals considerably went up at other observation epochs. In contrast, the LS residuals were on average smaller and more uniformly distributed. Thus, the LS solution was a better estimate of the orbit compared to the IOD solution, even when only few measurements distributed on a short arc were available.

Fig. 2

Statistics of the absolute value normalized residuals on $\alpha$ and $\delta$ for the IOD and DALS solutions. Observed object on a Molniya orbit

6.2 Confidence region representation

This section is devoted to analyze the representation of the confidence region. The object in Molniya orbit is used as test case, as it is characterized by the shortest observational arc. The DALS solver was run with 8 observations 40 s apart, and $\sigma =0.5$ arcsec. The DALS solution led to $J^*=5.008$. In confidence region definition, a value $K=3.1$ was chosen to ensure a confidence level of 95 percent (see Eqs. (8) and (25)). The state vector was represented in Cartesian coordinates, while results are shown on the $\rho -\dot{\rho }$ plane, where the largest uncertainty was expected (Milani et al. 2004; Worthy and Holzinger 2015).

First, the relevance of high-order terms was evaluated. Using a third-order polynomial approximation of J and a cloud of 50,000 samples led to $\varGamma _H=0.563$, which means that the relative impact of the third-order terms was around $56\%$. This suggested that high-order terms were relevant for an accurate analysis, and a high-order description of the confidence region should be adopted. In contrast, the same test case performed with observations 420 s apart (i.e., spread over a longer arc) led to $\varGamma _H=0.003$.

Next, the algorithm described in Sect. 4.1.1 was run. The polynomial approximation of J was recomputed five times to ensure an estimated truncation error of $10^{-2}$. The resulting $\mathbf{LOV}_1$ is plotted in Fig. 3 and compared against the semi-major axis of the second-order ellipsoid. The curvature and stretching of $\mathbf{LOV}_1$ led to $\varGamma _{LOV_{1}}=0.119$. If we replace the second-order approximation of J with its 6th-order counterpart in the calculation of this index without recomputing the polynomial, we obtain a value of 0.169. This result further proved the need for recalculating the Taylor expansions to achieve accurate results. The same algorithm was run along ${\varvec{v}}_2$, the second main direction of uncertainty. The resulting set of points is plotted in Fig. 4. These points mostly lay on the axis of the ellipsoid, giving $\varGamma _{LOV_{2}}=0.0021$. Consequently, it was not necessary to run the algorithm along ${\varvec{v}}_3$. In case of observations spread over a long arc, also the first LOV lay on the semi-major axis (see Fig. 5), leading to $\varGamma _{LOV_{1}}=0.0015$. This confirmed that the second-order approximation was accurate enough in case of long observation arc.

The third step was evaluating the uncertainty set’s dimensionality by computing $\varGamma _D^i$. The confidence region was very large along ${\varvec{v}}_1$, with $\varGamma _D^1={481}^{\circ }$. $\varGamma _D^2$ was ${49}^{\circ }$, while $\varGamma _D^i\approx {0.1}^{\circ }-{0.2}^{\circ }$ for $i=3,\ldots ,6$. Thus, a two-dimensional description of the confidence region seemed to be appropriate. The confidence region turned out to be much smaller for the long observation arc. Along ${\varvec{v}}_1$, $\varGamma _D^1={3.73}^{\circ }$, whereas along the other directions $\varGamma _D^i\le {0.5}^{\circ }$ for $i=2,\dots ,6$. A mono-dimensional approximation of the confidence region may thus be sufficiently accurate in the case of long arc.

Fig. 3

$\mathbf{LOV}_1$ and semi-major axis of the second-order ellipsoid in the $\rho -\dot{\rho }$ plane for an object in Molniya orbit (NORAD Catalog number 40296). The DALS was run with 8 observations 40 s apart and $\sigma =0.5$ arcsec

Fig. 4

$\mathbf{LOV}_2$ and second axis of the second-order ellipsoid in the $\rho -\dot{\rho }$ plane for an object in Molniya orbit (NORAD Catalog number 40296). The DALS was run with 8 observations 40 s apart and $\sigma =0.5$ arcsec

Fig. 5

$\mathbf{LOV}_1$ and semi-major axis of the second-order ellipsoid in the $\rho -\dot{\rho }$ plane for an object in Molniya orbit (NORAD Catalog number 40296). The DALS was run with 8 observations 420 s apart and $\sigma =0.5$ arcsec

As the confidence region was shown to be two-dimensional in the short arc case, the methods introduced in Sect. 4 can be applied to fully characterize the uncertainty set. In Fig. 6, samples generated with a second-order approximation are plotted in the $\rho -\dot{\rho }$ plane, while the performances of the algorithms described in Sect. 4 are compared in Fig. 7. The second-order approximation did not allow us to sample the whole uncertainty set, as suggested by the value of $\varGamma _H$. In contrast, both the GES and AD algorithms provided a more reliable description of the region. The two high-order methods performed equally well because $\varGamma _{LOV}^2$ was very small, meaning that nonlinearities could be neglected along ${\varvec{v}}_2$. The higher computational cost of the GES could thus be avoided. Table 4 shows the computational time of the algorithms obtained on a Windows desktop with a 3.20 GHz Intel i5-6500 processor and 16 GB memory. Note that polynomial evaluations were performed in MATLAB, and not optimized for efficiency.

Fig. 6

Sampling of the confidence region based on a second-order approximation. The colormap refers to $e^{-(J_i-J^*)}$. The object was in Molniya orbit (NORAD Catalog number 40296), and the DALS was run with 8 observations 40 s apart and $\sigma =0.5$ arcsec

Fig. 7

Sampling of the confidence region by means of GES algorithm and AD algorithm. The colormap refers to $e^{-(J_i-J^*)}$. The object was in Molniya orbit (NORAD Catalog number 40296), and the DALS was run with 8 observations 40 s apart and $\sigma =0.5$ arcsec

Table 4 Computational time of the different sampling algorithms. In each column, the number of times an operation was run in the corresponding algorithm is reported

The next analysis considers the representation of the full n-dimensional uncertainty region by ADS. The first step was to enclose the uncertainty domain with a box defined in the eigenvector space. This was achieved by considering the enclosure of the LOVs and the second-order ellipsoid. The ADS was then run to obtain an accurate polynomial representation of J on the entire domain, using $10^{-2}$ as accuracy threshold of the estimated truncation error. In Fig. 8, the resulting subdomains are shown both in the $\rho -\dot{\rho }$ and ${\varvec{v}}_1-{\varvec{v}}_2$ planes. Subdomains in white were discarded (minimum larger than the confidence region threshold), while colored subdomains were retained. The colormap refers to the ratio $\frac{J^*}{J_i}$, with $J_i$ being the minimum value of J within each subdomain. The domain was only split along ${\varvec{v}}_1$, the main direction of uncertainty. The LOV crossed 5 subdomains, the same number of times the polynomial expansion of J was recomputed when running the LOV algorithm.

Within the domain, the accurate representation of the target function allowed us to obtain the solution pdf using Eq. (37) once the integral of Eq. (38) is computed. In this case, we used $5\times 10^4$ samples and computed $\int _D e^{-\frac{1}{2}\mathcal {T}^{k}_{\delta J} ({\varvec{x}})}d{\varvec{x}} = 4.6\times 10^{-7}$. The relative difference with respect to the second-order value provided by $\sqrt{\frac{(2\pi )^n}{\left| C\right| }}$ was 0.084. For the long-arc case, the relative difference reduced to $4\times 10^{-12}$.

Fig. 8

Splitting of the domain in the $\rho -\dot{\rho }$ and ${\varvec{v}}_1-{\varvec{v}}_2$ planes performed by the ADS, compared against the LOV. The colormap refers to the value of J. The color of the subdomains depends on the ratio $\frac{J*}{J_i}$, with $J_i$ being the minimum value of J within the subdomain, while white subdomains were discared. The observed object was in Molniya orbit (NORAD Catalog number 40296) and the DALS was run with 8 observations 40 s apart and $\sigma =0.5$ arcsec

6.3 Effect of state representation

The choice of state representation significantly affected the confidence region description. In Sect. 6.2, the polynomial approximation of J was expressed in Cartesian coordinates, in which the effect of high-order terms was found to be less relevant. However, the MEE representation is a more suitable choice when it comes to propagating the confidence region. MEE absorb part of the nonlinearity of orbital dynamics and, thus, bring benefits when propagating the region (Vittaldev et al. 2016). In this section, the same object as in Sect. 6.2 is analyzed. However, the state vector was expressed in MEE.

The third-order polynomial approximation of J led to $\varGamma _H\approx \infty$, meaning that the size of third-order terms was large and the accuracy of the Taylor expansion low (the approximation of J also assumed negative values within the sampled domain, which explains the very large number obtained for $\varGamma _H$). In Figs. 9, 10, the resulting LOVs along ${\varvec{v}}_1$ and ${\varvec{v}}_2$ are plotted and compared against the axes of the second-order ellipsoid on the plane $\rho -\dot{\rho }$. The $\mathbf{LOV}_1$ strongly differed from the semi-major axis of the ellipsoid, more than with Cartesian coordinates (compare Fig. 9 with Fig. 3). The corresponding value of $\varGamma _{LOV_{1}}$ was 0.983. As shown in Fig. 10, the $\mathbf{LOV}_2$ also diverged from the ellipsoid axis, with $\varGamma _{LOV_{2}}=0.686$, while the effect of high-order terms along ${\varvec{v}}_3$ was negligible (with $\varGamma _{LOV_{3}}=1\times 10^{-4}$). Note that the ellipsoid axes computed in MEE coordinates were not straight lines when projected onto the $\rho -\dot{\rho }$ plane due to the nonlinearities in the coordinate transformation. This is also the reason why MEE are less appropriate in confidence description.

As for the uncertainty set’s dimensionality, the size of the confidence region along ${\varvec{v}}_1$ was such that $\varGamma _D^1={562}^{\circ }$, thus comparable to the confidence region with Cartesian coordinates. In contrast, along ${\varvec{v}}_2$ the confidence region in MEE was smaller, with $\varGamma _D^2={2.4}^{\circ }$. Along the other directions, $\varGamma _D^i\le {0.3}^{\circ }$ for $i=3,\dots ,6$. Thus, also with MEE a two-dimensional approximation of the confidence region seemed to be reasonable with short arc.

The GES algorithm was more accurate than the AD algorithm in sampling the uncertainty set, due to the relevance of high-order terms along ${\varvec{v}}_2$. Figure 11 compares the two resulting samplings. The GES algorithm succeeded in generating samples in the whole uncertainty region, so justifying its computational cost. It is worth noting that Fig. 11 is related to a scenario in which observations are 60 s apart rather than 40. This choice was adopted because, in the latter case where the GES algorithm was applied to the MEE representation, the solution of the nonlinear system in Eq. (35) failed to converge for some points of the uncertainty set.

In summary, the Cartesian coordinates proved to be a more suitable choice when it came to describe the confidence region of an OD solution, with nonlinearities playing a less relevant role. However, also with Cartesian coordinates, a high-order approach is recommended when accurate results are required.

Fig. 9

$\mathbf{LOV}_1$ and semi-major axis of the second-order ellipsoid in the $\rho -\dot{\rho }$ plane for an object in Molniya orbit (NORAD Catalog number 40296). The DALS was run with 8 observations 40 s apart and $\sigma =0.5$ arcsec, using MEE

Fig. 10

$\mathbf{LOV}_2$ and second axis of the second-order ellipsoid in the $\rho -\dot{\rho }$ plane for an object in Molniya orbit (NORAD Catalog number 40296). The DALS was run with 8 observations 40 s apart and $\sigma =0.5$ arcsec, using MEE

Fig. 11

Sampling of the confidence region by means of GES algorithm and AD algorithm. The colormap refers to $e^{-(J_i-J^*)}$. The object was in Molniya orbit (NORAD Catalog number 40296), and the DALS was run with 8 observations 60 s apart and $\sigma =0.5$ arcsec, using MEE

6.4 Effect of observation separation

In Sect. 6.2, analysis of the confidence region with short arc was compared to results obtained when observations were spread over a larger arc, suggesting that the observation separation may significantly affect the uncertainty set. In this section, the effect of the observation separation on the indices described in Sect. 5 is analyzed. The DALS solver was run with 8 observations of the object in Molniya orbit (NORAD Catalog number 40296) and $\sigma =0.5$ arcsec. Different angular separations were simulated. In Fig. 12, the trends of $\varGamma _H$ and $\varGamma _{LOV_{1}}$ for different observation separations are plotted. The effect of high-order terms significantly decreased for observations spread over a larger arc and, consequently, the LOV’s departure from the semi-major axis of the second-order confidence ellipsoid was less evident. The values of both indices were smaller when a Cartesian representation was adopted, meaning that Cartesian coordinates could allow us to neglect high-order terms with shorter arcs. In Fig. 12(a), $\varGamma _H$ tended toward infinity when MEE were used. This happened because the third-order approximation of J can turn into negative values within the domain of interest. It is a hint that we need to recompute the polynomial expression of J when running the LOV algorithm. In contrast, in Fig. 12(b), $\varGamma _{LOV_{1}}$ tended toward 1 because the term $e^{-\frac{1}{2}\mathcal {T}^{2}_{\delta J} \left( {\varvec{x}}_i^{LOV}\right) }$ became negligible with short arcs.

In Fig. 13, $\varGamma _D^1$, $\varGamma _D^2$ and $\varGamma _D^3$ are plotted. The values of these indices decreased for longer observation separations with both Cartesian coordinates and MEE, meaning that the uncertainty set shrank when observations were spread over a longer arc. $\varGamma _D^3$ was also relatively small with short observational arcs, which justified the two-dimensional description of the confidence region suggested in this work. Finally, it is worth noting that, with longer arcs, $\varGamma _D^2$ became small enough that also the second dimension was negligible. This behavior was more evident when MEE were used, showing that a mono-dimensional representation may be appropriate in this case, due to the alignment of one coordinate with the semi-major axis.

Fig. 12

Trends of $\varGamma _H$ and $\varGamma _{LOV_{1}}$ as functions of observation separation for both Cartesian and MEE representation. Values larger than $10^6$ were omitted

Fig. 13

Trend of $\varGamma _D$ as a function of observation separation for both Cartesian and MEE representation

7 Conclusions

In this work, we focused our investigation on the OD problem when optical observations are taken on observation arcs that are long enough to solve a least square problem, but too short to accurately determine the orbits.

We formulated a classical LS problem and implemented an arbitrary-order solver (referred to as DALS solver). In doing so, we avoided the approximation of classical differential correction methods. The formulation of a LS problem and its solution via the DALS improved on average the available IOD solution. Thus, including all acquired observations in the OD process turned out to be useful even on short arcs.

We have introduced nonlinear methods in the representation of the LS solution’s confidence region. DA techniques allowed us to retain high-order terms in the polynomial approximation of the target function. These terms are typically neglected by linearized theories, but they can be relevant for the accurate description of the confidence region of orbits determined with short arcs.

To this aim, we have introduced four algorithms based on DA techniques to nonlinearly describe the confidence region. The first one is a DA-based implementation of the LOV. We used DA to effectively solve the set of nonlinear equations required to capture the departure of the LOV from the axis of the second-order ellipsoid. In this algorithm, the polynomial approximation of the target function is recomputed only when necessary, based on accuracy requirements. The concept of LOV was then extended to two dimensions, introducing the GES. Another approach combined the LOV with a high-order polynomial to obtain a two-dimensional sampling without the computational cost of GES. Finally, a method was proposed to fully enclose the n-dimensional uncertainty set and accurately represent the target function over it by using ADS.

As high-order computations require extra computational cost, we have introduced an index to guide the choice between second-order and high-order representation of the uncertainty set. Through this index, it was shown that the effect of nonlinearities decreases significantly for longer observational arc and that Cartesian coordinates are a better choice than MEE. An additional index was introduced to determine the uncertainty set’s dimensionality based on the along-track dispersion associated with uncertainties in the determination of the orbit semi-major axis. This choice is strongly connected with the possibility of acquiring follow-up observations. Analysis of the dimensionality index demonstrated that a two-dimensional representation of the uncertainty region can be sufficiently accurate, depending on the telescope properties and the adopted observation strategy. With longer arcs, the uncertainty region could even be approximated as a mono-dimensional set, in particular when MEE are used.

The methods we have introduced come at the cost of intensive computations and the loss of a closed-form representation of the state statistics. However, the accuracy gained by the retention of nonlinear terms may play a key role in the development of reliable tools for observations correlation and for the initialization of nonlinear state estimation techniques, such as a particle filter. Future effort will be dedicated to the development of a full nonlinear mapping between sensor noise and object state, which will allow us to consider measurement noise with arbitrary statistics.