Skip to main content
SpringerLink
Log in

Equilibrium points and associated periodic orbits in the gravity of binary asteroid systems: (66391) 1999 KW4 as an example

  • Original Article
  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

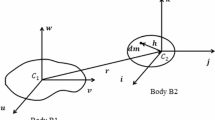
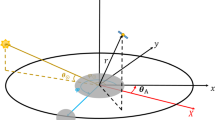
Abstract

The motion of a massless particle in the gravity of a binary asteroid system, referred as the restricted full three-body problem (RF3BP), is fundamental, not only for the evolution of the binary system, but also for the design of relevant space missions. In this paper, equilibrium points and associated periodic orbit families in the gravity of a binary system are investigated, with the binary (66391) 1999 KW4 as an example. The polyhedron shape model is used to describe irregular shapes and corresponding gravity fields of the primary and secondary of (66391) 1999 KW4, which is more accurate than the ellipsoid shape model in previous studies and provides a high-fidelity representation of the gravitational environment. Both of the synchronous and non-synchronous states of the binary system are considered. For the synchronous binary system, the equilibrium points and their stability are determined, and periodic orbit families emanating from each equilibrium point are generated by using the shooting (multiple shooting) method and the homotopy method, where the homotopy function connects the circular restricted three-body problem and RF3BP. In the non-synchronous binary system, trajectories of equivalent equilibrium points are calculated, and the associated periodic orbits are obtained by using the homotopy method, where the homotopy function connects the synchronous and non-synchronous systems. Although only the binary (66391) 1999 KW4 is considered, our methods will also be well applicable to other binary systems with polyhedron shape data. Our results on equilibrium points and associated periodic orbits provide general insights into the dynamical environment and orbital behaviors in proximity of small binary asteroids and enable the trajectory design and mission operations in future binary system explorations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30

Similar content being viewed by others

References

  • Bellerose, J.: The restricted full three body problem: applications to binary asteroid exploration. PhD thesis, University of Michigan (2008)

  • Bellerose, J., Scheeres, D.J.: Periodic orbits in the vicinity of the equilateral points of the restricted full three-body problem. In: AAS/AIAA Conference, Lake Tahoe, California, AAS-05-295, vol. 711 (2005)

  • Bellerose, J., Scheeres, D.: General dynamics in the restricted full three body problem. Acta Astronaut. 62(10), 563–576 (2008a)

    Article  ADS  MATH  Google Scholar 

  • Bellerose, J., Scheeres, D.J.: Restricted full three-body problem: application to binary system 1999 KW4. J. Guid. Control Dyn. 31(1), 162–171 (2008b)

    Article  ADS  Google Scholar 

  • Chanut, T., Winter, O., Amarante, A., Araújo, N.: 3d plausible orbital stability close to asteroid (216) Kleopatra. Mon. Not. R. Astron. Soc. 452(2), 1316–1327 (2015)

    Article  ADS  Google Scholar 

  • Chapman, C., Veverka, J., Thomas, P., Klaasen, K., et al.: Discovery and physical properties of Dactyl, a satellite of asteroid 243 Ida. Nature 374(6525), 783 (1995)

    Article  ADS  Google Scholar 

  • Chappaz, L., Howell, K.: Trajectory exploration within binary systems comprised of small irregular bodies. In: 23rd AAS/AIAA Space Flight Mechanics Meeting, Kauai, Hawaii (2013)

  • Chappaz, L., Howell, K.C.: Exploration of bounded motion near binary systems comprised of small irregular bodies. Celest. Mech. Dyn. Astron. 123(2), 123–149 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  • Ćuk, M., Nesvornỳ, D.: Orbital evolution of small binary asteroids. Icarus 207(2), 732–743 (2010)

    Article  ADS  Google Scholar 

  • Dichmann, D., Doedel, E., Paffenroth, R.: The computation of periodic solutions of the 3-body problem using the numerical continuation software auto. Libration Point Orbits and Applications, pp. 429–488 (2003)

  • Doedel, E., Keller, H.B., Kernevez, J.P.: Numerical analysis and control of bifurcation problems (i): bifurcation in finite dimensions. Int. J. Bifurc. Chaos 1(03), 493–520 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  • Doedel, E.J., Romanov, V.A., Paffenroth, R.C., Keller, H.B., Dichmann, D.J., Galán-Vioque, J., et al.: Elemental periodic orbits associated with the libration points in the circular restricted 3-body problem. Int. J. Bifurc. Chaos 17(08), 2625–2677 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  • Fahnestock, E.G.: The full two-body-problem: simulation, analysis, and application to the dynamics, characteristics, and evolution of binary asteroid systems. PhD thesis, University of Michigan (2009)

  • Fahnestock, E.G., Scheeres, D.J.: Simulation and analysis of the dynamics of binary near-earth asteroid (66391) 1999 KW4. Icarus 194(2), 410–435 (2008)

    Article  ADS  Google Scholar 

  • Gómez, G., Mondelo, J.M.: The dynamics around the collinear equilibrium points of the RTBP. Physica D 157(4), 283–321 (2001)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Hénon, M.: Generating Families in the Restricted Three-Body Problem, vol. 52. Springer, Berlin (2003)

    MATH  Google Scholar 

  • Hou, X., Liu, L.: Bifurcating families around collinear libration points. Celest. Mech. Dyn. Astron. 116(3), 241–263 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  • Howell, K.C.: Three-dimensional, periodic, ‘halo’ orbits. Celest. Mech. 32(1), 53–71 (1984)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Jacobson, S.A., Scheeres, D.J.: Dynamics of rotationally fissioned asteroids: source of observed small asteroid systems. Icarus 214(1), 161–178 (2011a)

    Article  ADS  Google Scholar 

  • Jacobson, S.A., Scheeres, D.J.: Long-term stable equilibria for synchronous binary asteroids. Astrophys. J. Lett. 736(1), L19 (2011b)

    Article  ADS  Google Scholar 

  • Jacobson, S.A., Scheeres, D.J., McMahon, J.: Formation of the wide asynchronous binary asteroid population. Astrophys. J. 780(1), 60 (2013)

    Article  ADS  Google Scholar 

  • Jiang, Y., Baoyin, H.: Periodic orbit families in the gravitational field of irregular-shaped bodies. Astron. J. 152(5), 137 (2016)

    Article  ADS  Google Scholar 

  • Jiang, Y., Baoyin, H., Li, H.: Periodic motion near the surface of asteroids. Astrophys. Space Sci. 360(2), 63 (2015a)

    Article  ADS  Google Scholar 

  • Jiang, Y., Yu, Y., Baoyin, H.: Topological classifications and bifurcations of periodic orbits in the potential field of highly irregular-shaped celestial bodies. Nonlinear Dyn. 81(1–2), 119–140 (2015b)

    Article  MathSciNet  MATH  Google Scholar 

  • Koon, W.S., Lo, M.W., Marsden, J.E., Ross, S.D.: Dynamical Systems, the Three-Body Problem and Space Mission Design. Marsden Books, Wellington (2008)

    MATH  Google Scholar 

  • Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory, vol. 112. Springer, Berlin (2013)

    Google Scholar 

  • Liu, X., Baoyin, H., Ma, X.: Periodic orbits in the gravity field of a fixed homogeneous cube. Astrophys. Space Sci. 334(2), 357–364 (2011)

    Article  ADS  MATH  Google Scholar 

  • Margot, J.L., Nolan, M., Benner, L., Ostro, S., Jurgens, R., Giorgini, J., et al.: Binary asteroids in the near-earth object population. Science 296(5572), 1445–1448 (2002)

    Article  ADS  Google Scholar 

  • McMahon, J., Scheeres, D.: Detailed prediction for the BYORP effect on binary near-earth asteroid (66391) 1999 KW4 and implications for the binary population. Icarus 209(2), 494–509 (2010a)

    Article  ADS  Google Scholar 

  • McMahon, J., Scheeres, D.: Secular orbit variation due to solar radiation effects: a detailed model for BYORP. Celest. Mech. Dyn. Astron. 106(3), 261–300 (2010b)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Ni, Y., Jiang, Y., Baoyin, H.: Multiple bifurcations in the periodic orbit around Eros. Astrophys. Space Sci. 361(5), 170 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  • Ostro, S.J., Margot, J.L., Benner, L.A., Giorgini, J.D., Scheeres, D.J., Fahnestock, E.G., et al.: Radar imaging of binary near-earth asteroid (66391) 1999 KW4. Science 314(5803), 1276–1280 (2006)

    Article  ADS  Google Scholar 

  • Peng, H., Xu, S.: Stability of two groups of multi-revolution elliptic halo orbits in the elliptic restricted three-body problem. Celest. Mech. Dyn. Astron. 123(3), 279–303 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  • Pravec, P., Harris, A.W.: Binary asteroid population: 1. Angular momentum content. Icarus 190(1), 250–259 (2007)

    Article  ADS  Google Scholar 

  • Scheeres, D.J.: Orbital Motion in Strongly Perturbed Environments: Applications to Asteroid, Comet and Planetary Satellite Orbiters. Springer, Berlin (2016)

    Google Scholar 

  • Scheeres, D., Williams, B., Miller, J.: Evaluation of the dynamic environment of an asteroid: applications to 433 Eros. J. Guid. Control Dyn. 23(3), 466–475 (2000)

    Article  ADS  Google Scholar 

  • Scheeres, D.J., Fahnestock, E.G., Ostro, S.J., Margot, J.L., Benner, L.A., Broschart, S.B., et al.: Dynamical configuration of binary near-earth asteroid (66391) 1999 KW4. Science 314(5803), 1280–1283 (2006)

    Article  ADS  Google Scholar 

  • Scheeres, D., Van Wal, S., Olikara, Z., Baresi, N.: The dynamical environment for the exploration of Phobos, ists-2017-d-007. International Symposium on Space Technology and Science. Ehime, Japan, pp. 3–9 (2017)

  • Szebehely, V.: Theory of Orbit: The Restricted Problem of Three Bodies. Elsevier, Amsterdam (2012)

    MATH  Google Scholar 

  • Vaquero, M., Howell, K.C.: Design of transfer trajectories between resonant orbits in the Earth–Moon restricted problem. Acta Astronaut. 94(1), 302–317 (2014)

    Article  ADS  Google Scholar 

  • Werner, R.A., Scheeres, D.J.: Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia. Celest. Mech. Dyn. Astron. 65(3), 313–344 (1996)

    ADS  MATH  Google Scholar 

  • Woo, P., Misra, A.K.: Equilibrium points in the full three-body problem. Acta Astronaut. 99, 158–165 (2014)

    Article  ADS  Google Scholar 

  • Woo, P., Misra, A.K.: Bounded trajectories of a spacecraft near an equilibrium point of a binary asteroid system. Acta Astronaut. 110, 313–323 (2015)

    Article  ADS  Google Scholar 

  • Yu, Y., Baoyin, H.: Generating families of 3d periodic orbits about asteroids. Mon. Not. R. Astron. Soc. 427(1), 872–881 (2012)

    Article  ADS  Google Scholar 

  • Yu, Y., Baoyin, H., Jiang, Y.: Constructing the natural families of periodic orbits near irregular bodies. Mon. Not. R. Astron. Soc. 453(3), 3269–3277 (2015)

    Article  ADS  Google Scholar 

  • Zamaro, M., Biggs, J.: Natural motion around the Martian moon Phobos: the dynamical substitutes of the libration point orbits in an elliptic three-body problem with gravity harmonics. Celest. Mech. Dyn. Astron. 122(3), 263–302 (2015)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work has been supported by the National Natural Science Foundation of China under Grants 11432001 and 11602009, the Young Elite Scientist Sponsorship Program by China Association for Science and Technology, and the Fundamental Research Funds for the Central Universities.

Author information

Authors and Affiliations

  1. School of Astronautics, Beihang University, Beijing, 100083, China

    Yu Shi, Yue Wang & Shijie Xu

Authors
  1. Yu Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yue Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shijie Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yue Wang.

Ethics declarations

Conflict of interest

We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the paper submitted.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shi, Y., Wang, Y. & Xu, S. Equilibrium points and associated periodic orbits in the gravity of binary asteroid systems: (66391) 1999 KW4 as an example. Celest Mech Dyn Astr 130, 32 (2018). https://doi.org/10.1007/s10569-018-9827-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10569-018-9827-7

Keywords

Search

Navigation