Skip to main content
SpringerLink
Log in

Stability of the Euler resting N-body relative equilibria

  • Original Article
  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

A Correction to this article was published on 20 August 2018

This article has been updated

Abstract

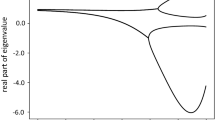
The stability of a system of N equal-sized mutually gravitating spheres resting on each other in a straight line and rotating in inertial space is considered. This is a generalization of the “Euler Resting” configurations previously analyzed in the finite density 3 and 4 body problems. Specific questions for the general case are how rapidly the system must spin for the configuration to stabilize, how rapidly it can spin before the components separate from each other, and how these results change as a function of N. This paper shows that the Euler Resting configuration can only be stable for up to 5 bodies and that for 6 or more bodies the configuration can never be stable. This places an ideal limit of 5:1 on the aspect ratio of a rubble pile body’s shape.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Change history

  • 20 August 2018

    Due to an error in a supporting algorithm used in writing the paper there was an incorrect conclusion given which is corrected here.

References

  • de Lagrange, J.L.: Theorie de la libration de la lune. In: Serret, J.A., Darboux, G. (eds.) Lagrange JL (1867–1892) Oeuvres de Lagrange, pp. 5–124. Paris, Gauthier-Villars (1780)

  • Duboshin, G.N.: The differential equations of translational-rotational motion of mutally attracting rigid bodies. Sov. Astron. 2, 239 (1958)

    ADS  Google Scholar 

  • Fujiwara, A., Kawaguchi, J., Yeomans, D.K., Abe, M., Mukai, T., Okada, T., et al.: The rubble-pile asteroid Itokawa as observed by Hayabusa. Science 312(5778), 1330–1334 (2006)

    Article  ADS  Google Scholar 

  • Jeffrey, A.: Beck and Christopher D Hall. Relative equilibria of a rigid satellite in a circular keplerian orbit. J. Astronaut. Sci. 46(3), 215–247 (1998)

    MathSciNet  Google Scholar 

  • Maciejewski, A.J.: Reduction, relative equilibria and potential in the two rigid bodies problem. Celest. Mech. Dyn. Astron. 63(1), 1–28 (1995)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Moeckel, R.: Minimal energy configurations of gravitationally interacting rigid bodies. Celest. Mech. Dyn. Astron. 128(1), 3–18 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Moulton, F.R.: Periodic Orbits. Carnegie Institution of Washington (1920)

  • Scheeres, D.J.: Stability in the full two-body problem. Celest. Mech. Dyn. Astron. 83(1), 155–169 (2002)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Scheeres, D.J.: Minimum energy asteroid reconfigurations and catastrophic disruptions. Planet. Space Sci. 57(2), 154–164 (2009)

    Article  ADS  Google Scholar 

  • Scheeres, D.J.: Minimum energy configurations in the \(N\)-body problem and the Celestial mechanics of granular systems. Celest. Mech. Dyn. Astron. 113(3), 291–320 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Scheeres, D.J.: Relative equilibria in the full \(N\)-body problem with applications to the equal mass problem. In: Chyba, M., Bonnard, B. (eds.) Recent Advances in Celestial and Space Mechanics, vol. 23, pp. 31–81. Springer, Switzerland (2016a)

  • Scheeres, D.J.: Relative equilibria in the spherical, finite density three-body problem. J. Nonlinear Sci. 26, 1445–1482 (2016b)

  • Smale, S.: Topology and mechanics. I. Invent. Math. 10(4), 305–331 (1970a)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Smale, S.: Topology and mechanics. II. Invent. Math. 11(1), 45–64 (1970b)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Wang, L.S., Krishnaprasad, P.S., Maddocks, J.H.: Hamiltonian dynamics of a rigid body in a central gravitational field. Celest. Mech. Dyn. Astron. 50(4), 349–386 (1990)

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This research was supported by NASA grant NNX14AL16G.

Author information

Authors and Affiliations

  1. Smead Department of Aerospace Engineering Sciences, The University of Colorado Boulder, 429 UCB, Boulder, CO, USA

    D. J. Scheeres

Authors
  1. D. J. Scheeres
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. J. Scheeres.

Ethics declarations

Conflict of interest

The author declares no conflict of interest.

Additional information

This article is part of the topical collection on Close Approaches and Collisions in Planetary Systems.

Guest Editors: Giovanni Federico Gronchi, Ugo Locatelli, Giuseppe Pucacco and Alessandra Celletti.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Scheeres, D.J. Stability of the Euler resting N-body relative equilibria. Celest Mech Dyn Astr 130, 26 (2018). https://doi.org/10.1007/s10569-018-9819-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10569-018-9819-7

Keywords

Search

Navigation