Abstract
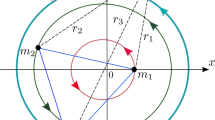
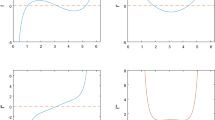
This study relates to equal-mass four-body orbits close to a quadruple central configuration. Locally, these orbits can be approximated by a perturbation from the homothetic quadruple collision/expansion orbit. Appropriate expressions are derived and the equal-mass four-body Siegel exponents and associated eigenmodes are presented.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Albouy, A.: Symétrie des configurations centrales de quadre corps. C. R. Acad. Sci. Paris 320, 217–220 (1995)
Albouy, A.: The symmetric central configurations of four equal masses. Contemp. Math. 198, 131–135 (1996)
Heggie, D.C., Sweatman, W.L.: Three-body scattering near triple collision or expansion. Mon. Not. R. Astron. Soc. 250, 555–575 (1991)
Lehmann-Filhés, R.: Ueber zwei Fälle des Vielkörperproblems. Astron. Nach. 127, 137–144 (1891)
McGehee, R.: Triple collision in the collinear three-body problem. Invent. Math. 27, 191–227 (1974)
Mikkola, S.: Encounters of binaries-I. Equal energies. Mon. Not. R. Astron. Soc. 203, 1107–1121 (1983)
Moeckel, R.: Central Configurations. Scholarpedia. http://www.scholarpedia.org/article/Central_configurations (2014)
Moulton, F.R.: The straight line solutions of the problem of N bodies. Ann. Math. 12, 1–17 (1910)
Siegel, C.L.: Der Dreierstoss. Ann. Math. 42, 127–168 (1940)
Siegel, C.L., Moser, J.K.: Lectures on Celestial Mechanics. Springer, Berlin (1971)
Simó, C., Lacomba, E.: Analysis of some degenerate quadruple collisions. Celest. Mech. 28, 49–62 (1982)
Sweatman, W.L.: Full ionisation in binary-binary encounters of equal masses with a small positive total energy. Mon. Not. R. Astron. Soc. 377, 459–464 (2007)
Waldvogel, J.: The close triple approach. Celest. Mech. 11, 429–432 (1975)
Waldvogel, J.: The three-body problem near triple collision. Celest. Mech. 14, 287–300 (1976)
Waldvogel, J.: The variational equation of the three-body problem. Celest. Mech. 21, 171–175 (1980)
Waldvogel, J.: The variational equation of the three-body problem. Celest. Mech. 28, 69–82 (1982)
Waldvogel, J.: Central configurations revisited. In: Steves, B.A., Maciejewski, A.J. (eds.) The Restless Universe: Applications of Gravitational N-Body Dynamics to Planetary, Stellar and Galactic Systems, pp. 285–299. Institute of Physics Publishing, Bristol (2001). ISBN 0-7503-0822-2
Acknowledgments
The author is grateful to Douglas Heggie and the University of Edinburgh and Bonnie Steves and Glasgow Caledonian University for their hospitality while progressing this research. He also thanks the organisers and participants of Celmec VI: San Martino al Cimino, Viterbo, Italy for fruitful discussions and the referees of this paper for their constructive comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sweatman, W.L. Orbits near central configurations for four equal masses. Celest Mech Dyn Astr 119, 379–395 (2014). https://doi.org/10.1007/s10569-014-9556-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-014-9556-5