Skip to main content
SpringerLink
Log in

Dynamics of a small body under the action of a Maxwell ring-type N-body system with a spheroidal central body

  • Original Article
  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

Abstract

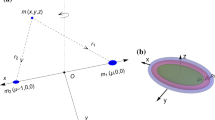
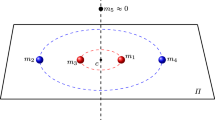
This study outlines some aspects of the dynamics of a small body under the action of a Maxwell-type N-body system with a spheroidal central body. The non-sphericity of the central primary is described by means of a corrective term in the Newton’s law of gravitation and is taken into account during the derivation of the equations of motion of the small body, improving in this way, previous treatments. Based on this new consideration we investigate the equilibrium locations of the small body and their parametric dependence, as well as the zero-velocity curves and surfaces for the planar motion, and the evolution of the regions where this motion is permitted when the Jacobian constant varies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Arribas, M., Elipe, A.: Bifurcations and equilibria in the extended N-body problem. Mech. Res. Commun. 31, 1–8 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  • Bang, D., Elmabsout, B.: Restricted N+1-body problem: existence and stability of relative equilibria. Celest. Mech. Dyn. Astron. 89, 305–318 (2004)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Barrabes, E., Cors, J.M., Hall, G.R.: A limit case of the “ring problem”: the planar circular restricted \((1+\text{ N })\) body problem. SIAM J. Appl. Dyn. Syst. 9(2), 634–658 (2010)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Barrio, R., Blesa, F., Serrano, S.: Qualitative analysis of the \((\text{ N }+1)\)-body ring problem. Chaos Solitons Fractals 36, 1067–1088 (2008)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Barrio, R., Blesa, F., Serrano, S.: Periodic, escape and chaotic orbits in the Copenhagen and the \((\text{ n }+1)\)-body ring problems. Commun. Nonlinear Sci. Numer. Simul. 14, 2229–2238 (2009)

    Google Scholar 

  • Bountis, T., Papadakis, K.E.: The stability of vertical motion in the N-body circular Sitnikov problem. Celest. Mech. Dyn. Astron. 104, 205–225 (2009)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Croustalloudi, M., Kalvouridis, T.: Attracting domains in ring-type N-body formations. Planet. Space Sci. 55(1–2), 53–69 (2007)

    Article  ADS  Google Scholar 

  • Elipe, A., Arribas, M., Kalvouridis, T.J.: Periodic solutions and their parametric evolution in the planar case of the \((\text{ n }+1)\) ring problem with oblateness. J. Guid. Control Dyn. 30(6), 1640–1648 (2007)

    Google Scholar 

  • Elmabsout, B.: Stability of some degenerate positions of relative equilibrium in the n-body problem. Dyn. Stab. Syst. 9(4), 315–319 (1994)

    Article  MathSciNet  Google Scholar 

  • Hadjifotinou, K.G., Kalvouridis, T.J.: Numerical investigation of periodic motion in the three-dimensional ring problem of N bodies. Int. J. Bifurcat. Chaos 15(8), 2681–2688 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  • Garcia-Azpeitia, C., Ize, J.: Global bifurcation of planar and spatial periodic solutions in the restricted n-body problem. Celest. Mech. Dyn. Astr. 110, 217–237 (2011)

    Article  MathSciNet  ADS  Google Scholar 

  • Haranas, I., Ragos, O., Mioc, V.: Yukawa-type potential effects in the anomalistic period of celestial bodies. Astrophys. Space Sci. 332, 107–113 (2011)

    Article  ADS  MATH  Google Scholar 

  • Kalvouridis, T.J.: A planar case of the n+1 body problem: the ‘ring’ problem. Astrophys. Space Sci. 260(3), 309–325 (1999)

    Article  ADS  Google Scholar 

  • Kalvouridis, T.J.: Particle motions in Maxwell’s ring dynamical systems. Celest. Mech. Dyn. Astron. 102(1–3), 191–206 (2008)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Maneff, G.: La gravitation et le principe de l’action et de la réaction. C.R. Acad. Sci. Paris 178, 2159–2161 (1924)

    MATH  Google Scholar 

  • Papadakis, K.E.: Asymptotic orbits in the (N+1)-body ring problem. Astrophys. Space Sci. 323, 261–272 (2009)

    Article  ADS  MATH  Google Scholar 

  • Pinotsis, A.D.: Evolution and stability of the theoretically predicted families of periodic orbits in the N-body ring problem. Astron. Astrophys. 432, 713–729 (2005)

    Article  ADS  MATH  Google Scholar 

  • Salo, H., Yoder, C.F.: The dynamics of co-orbital satellite systems. Astron. Astrophys. 205, 309–327 (1988)

    ADS  Google Scholar 

  • Scheeres, D.: On symmetric central configurations with application to satellite motion about rings. PhD Thesis, The University of Michigan (1992)

  • Vanderbei, R.J., Kolemen, E.: Linear stability of ring systems. Astron. J. 133, 656–664 (2007)

    Article  ADS  Google Scholar 

  • Vanderbei, R.J.: Linear stability of ring systems around oblate central masses. Adv. Space Res. 42, 1370–1377 (2008)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanics, Faculty of Applied Sciences, National Technical University of Athens, 5, Heroes of Polytechnion Ave., 157 73 , Athens, Greece

    Demetrios Gn. Fakis & Tilemahos J. Kalvouridis

Authors
  1. Demetrios Gn. Fakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tilemahos J. Kalvouridis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tilemahos J. Kalvouridis.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fakis, D.G., Kalvouridis, T.J. Dynamics of a small body under the action of a Maxwell ring-type N-body system with a spheroidal central body. Celest Mech Dyn Astr 116, 229–240 (2013). https://doi.org/10.1007/s10569-013-9484-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10569-013-9484-9

Keywords

Search

Navigation