Skip to main content
SpringerLink
Log in

Low-thrust propulsion in a coplanar circular restricted four body problem

  • Original Article
  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

Abstract

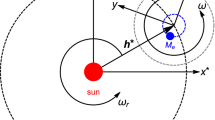
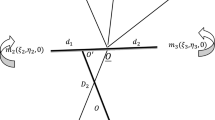
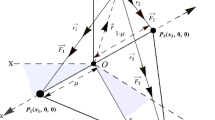
This paper formulates a circular restricted four body problem (CRFBP), where the three primaries are set in the stable Lagrangian equilateral triangle configuration and the fourth body is massless. The analysis of this autonomous coplanar CRFBP is undertaken, which identifies eight natural equilibria; four of which are close to the smaller body, two stable and two unstable, when considering the primaries to be the Sun and two smaller bodies of the Solar System. Following this, the model incorporates ‘near term’ low-thrust propulsion capabilities to generate surfaces of artificial equilibrium points close to the smaller primary, both in and out of the plane containing the celestial bodies. A stability analysis of these points is carried out and a stable subset of them is identified. Throughout the analysis the Sun-Jupiter-asteroid-spacecraft system is used, for conceivable masses of a hypothetical asteroid set at the libration point L 4. It is shown that eight bounded orbits exist, which can be maintained with a constant thrust less than 1.5 × 10−4 N for a 1000 kg spacecraft. This illustrates that, by exploiting low-thrust technologies, it would be possible to maintain an observation point more than 66% closer to the asteroid than that of a stable natural equilibrium point. The analysis then focusses on a major Jupiter Trojan: the (624) Hektor asteroid. The thrust required to enable close asteroid observation is determined in the simplified CRFBP model. Finally, a numerical simulation of the real Sun-Jupiter-(624) Hektor-spacecraft is undertaken, which tests the validity of the stability analysis of the simplified model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Alvarez-Ramirez, M., Vidal, C.: Dynamical aspects of an equilateral restricted four-body problem. Math. Probl. Eng. 2009, 1–23 (2009)

  • Ambrosetti A., Prodi G.: A Primer of Nonlinear Analysis, pp. 153–159. Cambridge University Press, Cambridge (1993)

    Google Scholar 

  • Andreu, M.A.: New results on computation of translunar Halo orbits of the real Earth-Moon system. In: Proceedings of the Conference Libration point orbits and applications, Aiguablava, pp. 225–237 (2002)

  • Arnold V.A., Kozolov V.V, Neishtadt A.I.: Mathematical Aspects of Classical and Celestial Mechanics. (Dynamical systems. III). Springer, Berlin (2006)

    Google Scholar 

  • Artin M.: Algebra, pp. 543–547. Prentice Hall, New Jersey (1991)

    Google Scholar 

  • Baig S., McInnes C.R.: Artificial three body equilibria for hybrid low-thrust propulsion. J. Guid. Contr. Dyn. 31(6), 1644–1655 (2008)

    Article  Google Scholar 

  • Baig S., McInnes C.R.: Artificial halo orbits for low-thrust propulsion spacecraft. Celest. Mech. Dyn. Astron. 104(4), 321–335 (2009)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Baltagiannis A.N., Papadakis K.E.: Equilibrium points and their stability in the restricted four body problem. Int. J. Bifurcat. Chaos. 21(8), 2179–2193 (2011)

    Article  Google Scholar 

  • Bombardelli C., Pelaez J.: On the stability of artificial equilibrium points in the circular restricted three-body problem. Celest. Mech. Dyn. Astron. 109(1), 13–26 (2011)

    Article  MathSciNet  ADS  Google Scholar 

  • Ceccaroni, M., Biggs, J.: Extension of low-thrust propulsion to the Autonomous Coplanar Circular Restricted Four Body Problem with application to future Trojan Asteroid missions. In: 61st International Astronautical Congress, IAC-10-1.1.3, Prague (2010)

  • Cronin J., Richards P.B., Russell L.H.: Some periodic solutions of a four-body problem. Icarus 3, 423 (1964)

    Article  MathSciNet  ADS  Google Scholar 

  • Dvorak, R., Schwarz, R., Lhotka, C.: On the dynamics of Trojan planets in extrasolar planetary systems. In: Proceedings of the IAU (International Astronomical Union) symposium, N. 249 (2008)

  • Erdi B., Forgács-Dajka E., Nagy I., Rajnai R.: A parametric study of stability and resonances around L4 in the elliptic restricted three-body problem. Celest. Mech. Dyn. Astron. 104, 145–158 (2009)

    Article  ADS  MATH  Google Scholar 

  • Fearn, D.G., Crookham, C.: The development of ion propulsion in the UK: a historical prespective. In: Proceedings of the 29th IEPC, Princeton (2005)

  • Gascheau M.: Examen d’une classe d’equations differentielles et application a un cas particulier du probleme des trois corps. C. R. Acad. Sci. 16, 343 (1843)

    Google Scholar 

  • Gomez, G., Jorba, A., Masdemont, J., Simó, C.: Dynamics and mission design near libration points vol. 4: advanced methods for triangular points. In: World Scientific Monograph Series in Mathematics, vol. 5, pp. 249–253 (2001)

  • Hadjidemetriou, J.D.: Instabilities in planetary-type orbits: applications to celestial mechanics. Instabilities in Dynamical Systems, Proceedings of the Advanced Study Institute, Cortina d’Ampezzo, pp. 135–163 (1978)

  • Hadjidemetriou J.D.: On periodic orbits and resonance in extrasolar planetary systems. Celest. Mech. Dyn. Astron. 102, 69–82 (2008)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Hadjidemetriou J.D., Psychoyos D., Voyatzis G.: The 1/1 resonance in extrasolar planetary systems. Celest. Mech. Dyn. Astron. 104, 23–38 (2009)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Hou X.Y., Liu L.: On quasi-periodic motions around the triangular libration points of the real EarthMoon system. Celest. Mech. Dyn. Astron. 108(3), 301–313 (2010)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Kloppenborg B., Stencel R., Monnier J.D., Schaefer G., Zhao M., Baron F. et al.: Infrared images of the transiting disk in the \({\epsilon}\) Aurigae system. Nature Lett. 464, 870–872 (2010)

    Article  ADS  Google Scholar 

  • Koon W.S., Lo M., Marsden J.E., Ross S.: Dynamical Systems, The Three-Body Problem and Space Mission Design, pp. 123–130. Marsden Books, London (2008)

    Google Scholar 

  • Marchal C.: Long term evolution of quasi-circular Trojan orbits. Celest. Mech. Dyn. Astron. 104, 53–67 (2009)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Marzari, F., Scholl, H., Murray, C., Lagerkvist, C.: Origin and evolution of Trojan asteroids, vol. 1, pp. 725–738. Asteroids III University of Arizona Press (2002)

  • Marzari F.: Puzzling Neptune Trojans. Science 313(5786), 451–452 (2006)

    Article  Google Scholar 

  • McInnes C.R., McDonald A.J., John F.L., MacDonald E.W.: Solar sail parking in restricted three-body systems. J. Guid. Contr. Dyn. 17(2), 399–406 (1994)

    Article  ADS  MATH  Google Scholar 

  • McKay, R., Macdonald, M., Bosquillon de Frescheville, F., Vasile, M., McInnes, C.R., Biggs, J.: Non-Keplerian orbits using low thrust, high ISP propulsion systems. In: 60th International Astronautical Congress, IAC-09-1.2.8, Daejeon (2009)

  • McKay R., Macdonald M., Biggs J., McInnes C.R.: Survey of highly non-Keplerian orbits with low-thrust propulsion. J. Guid. Contr. Dyn. 34(3), 645–666 (2011)

    Article  Google Scholar 

  • Melita M.D., Licandro J., Jones D.C., Williams I.P.: Physical properties and orbital stability of the Trojan asteroids. Icarus 195, 686–697 (2008)

    Article  ADS  Google Scholar 

  • Michalodimitrakis M.: The circular restricted four body problem. Astrophys. Space Sci. 75(2), 289–305 (1981)

    Article  ADS  Google Scholar 

  • Milani A., Nobili A.M.: On the stability of hierarchical four body systems. Celest. Mech. 31(3), 241–291 (1983)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Morimoto K., Yamakawa M.Y., Uesugi H.: Periodic orbits with low-thrust propulsion in the restricted three-body problem. J. Guid. Contr. Dyn. 29(5), 1131–1139 (2006)

    Article  Google Scholar 

  • Morimoto K., Yamakawa M.Y., Uesugi H.: Artificial equilibrium points in the low-thrust restricted three-body problem. J. Guid. Contr. Dyn. 30(5), 1563–1568 (2007)

    Article  Google Scholar 

  • Moulton F.R.: On a class of particular solutions of the problem of four bodies. Trans. Am. Math. Soc. 1, 17–29 (1900)

    Article  MathSciNet  MATH  Google Scholar 

  • Moulton F.R.: The straight line solutions of the problem of N bodies. Ann. Math. 12(3), 1–17 (1910)

    Article  MathSciNet  MATH  Google Scholar 

  • Nicolini, D.: LISA pathfinder field emission thruster system development program. In: Proceedings of the 30th International Electric Propulsion Conference, Florence (2007)

  • Papadakis K.E.: Asymptotic orbits in the restricted four body problem. Planet. Space Sci. 55(10), 1368–1379 (2007)

    Article  ADS  Google Scholar 

  • Piña E., Lonngi P.: Central configurations for the planar Newtonian four-body problem. Celest. Mech. Dyn. Astron. 108(1), 73–93 (2010)

    Article  ADS  MATH  Google Scholar 

  • Rivkin, A.S., Emery, J., Barucci, A., Bell, J.F., Bottke, W.F., Dotto, E., Gold, R., Lisse, C., Licandro, J., Prockter, L., Hibbits, C., Paul, M., Springmann, A., Yang, B.: The Trojan asteroids: keys to many locks, national academies of science in support of the national academies planetary science decadal survey 2013–2022, SBAG Community White Papers (2009)

  • Routh E.J.: On Laplace’s three particles, with a supplement on the stability of steady motion. Proc. Lond. Math. Soc. 6, 86–97 (1875)

    Article  MATH  Google Scholar 

  • Roy, A.E., Walker, I.W., MacDonald, A.J.C.: Studies on the stability of hierarchical dynamical systems. In: Proceedings of the Stability of the Solar System and Its Minor Natural and Artificial Bodies, pp. 151–174. Advanced Study Institute, Cortina d’Ampezzo (1985)

  • Scheeres D.J.: The restricted Hill four-body problem with applications to the earth moon sun system. Celest. Mech. Dyn. Astron. 70(2), 75–98 (1998)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Schwarz R., Suli A., Dvorak R.: Dynamics of possible Trojan planets in binary systems. Mon. Not. R. Astron. Soc. 398, 2085–2090 (2009)

    Article  ADS  Google Scholar 

  • Schwarz R., Süli Á., Dvorak R., Pilat-Lohinger E.: Stability of Trojan planets in multi-planetary systems Stability of Trojan planets in different dynamical systems. Celest. Mech. Dyn. Astron. 104(1–2), 69–84 (2009)

    Article  ADS  MATH  Google Scholar 

  • Shoemaker, E.M., Shoemaker, C.S., Wolfe, R.F.: Trojan asteroids: populations, dynamical structure and origin of the L4 and L5 swarms. Asteroids II, Proceedings of the Conference, Tucson (1988)

  • Simó C.: Relative equilibrium solutions in the four body problem. Celest. Mech. 18(2), 165–184 (1978)

    Article  ADS  MATH  Google Scholar 

  • Steves B.A., Roy A.E., Bell M.: Some special restricted four-body problems—I. Modelling the Caledonian problem. Planet. Space Sci. 46(11–12), 1465–1474 (1998)

    Article  ADS  Google Scholar 

  • Steves B.A., Roy A.E., Bell M.: Some special solutions of the four body problem—II. From Caledonia to Copenaghen. Planet. Space Sci. 46(11–12), 1475–1486 (1998)

    ADS  Google Scholar 

  • Van Hamme W., Wilson R.E.: The restricted four-body problem and epsilon Aurigae. Astroph. J. 306, 33–36 (1986)

    Article  ADS  Google Scholar 

  • Waters T., McInnes C.R.: Periodic orbits above the ecliptic plane in the solar sail restricted 3-body problem. J. Guid. Contr. Dyn. 30(3), 687–693 (2007)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Advanced Space Concepts Laboratory, University of Strathclyde, Glasgow, UK

    Marta Ceccaroni & James Biggs

Authors
  1. Marta Ceccaroni
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. James Biggs
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marta Ceccaroni.

Electronic Supplementary Material

The Below is the Electronic Supplementary Material.

ESM 1 (TEX 8 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ceccaroni, M., Biggs, J. Low-thrust propulsion in a coplanar circular restricted four body problem. Celest Mech Dyn Astr 112, 191–219 (2012). https://doi.org/10.1007/s10569-011-9391-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10569-011-9391-x

Keywords

Search

Navigation