Skip to main content
SpringerLink
Log in

Exact solution of a triaxial gyrostat with one rotor

  • Original Article
  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

Abstract

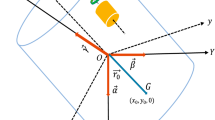
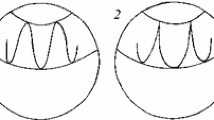
The problem of the attitude dynamics of a triaxial gyrostat under no external torques and one constant internal rotor, is a three degrees-of-freedom system, although thanks to the existence of integrals of motion it can be reduced to only one degree-of-freedom problem. We introduce coordinates to represent the orbits of constant angular momentum as a flow on a sphere. This representation shows that the problem is equivalent to a quadratic Hamiltonian depending on two parameters. We find the exact solution of the orbits in terms of elliptic functions. By making use of properties of elliptic functions we find the solution at each region of the parametric partition from the solution of one region. We also prove that heteroclinic orbits are planar curves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abad A., Elipe A., Vallejo M.: Automated Fourier series expansions for elliptic functions. Mech. Res. Commun. 21, 361–366 (1994)

    Article  MATH  Google Scholar 

  • Abad A., Elipe A., Vallejo M.: Normalization of perturbed non-linear Hamiltonian oscillators. Int. J. Nonlinear Mech. 32, 443–453 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  • Abad A., Elipe A., Palacián J., San-Juan J.F.: ATESAT: A symbolic processor for artificial satellite theory. Math. Comput. Simul. 45, 497–510 (1998)

    Article  MATH  Google Scholar 

  • Bowman F.: Introduction to Elliptic Functions with Applications. Dover Pub., New York (1961)

    MATH  Google Scholar 

  • Byrd P.F., Friedman M.D.: Handbook of Elliptic Integrals for Engineers an Physicists. Springer Verlag, Berlin (1954)

    Google Scholar 

  • Coffey S.L., Deprit A., Deprit E., Healy L.: Painting the phase space portrait of an integrable dynamical system. Science 247, 833–836 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  • Cochran J.E., Shu P.H., Rew S.D.: Attitude motion of asymmetric dual-spin spacecraft. J. Guid. Control Dyn. 5, 37–42 (1982)

    Article  MATH  Google Scholar 

  • Deprit A., Elipe A.: Complete reduction of the Euler–Poinsot problem. J. Astronaut. Sci. 41, 603–628 (1993)

    ADS  MathSciNet  Google Scholar 

  • Elipe A., Lanchares V.: Biparametric quadratic Hamiltonians on the unit sphere: complete classification. Mech. Res. Commun. 21, 209–214 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  • Elipe A., Lanchares V.: Phase flow of an axially symmetrical gyrostat with one constant rotor. J. Math. Phys. 38, 3533–3544 (1997a)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Elipe A., Lanchares V.: Two equivalent problems: Gyrostats in free motion and parametric quadratic Hamiltonians. Mech. Res. Commun. 24, 583–590 (1997b)

    Article  MathSciNet  MATH  Google Scholar 

  • Elipe A., Vallejo M.: On the attitude dynamics of perturbed triaxial rigid bodies. Celest. Mech. Dyn. Astron. 81, 3–12 (2001)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Frauendiener J.: Quadratic Hamiltonians on the unit sphere. Mech. Res. Commun. 22, 313–317 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  • Hall C.D.: Equivalence of two classes of dual-spin spacecraft spinup dynamics. J. Guid. Control Dyn. 15, 1032–1034 (1992)

    Article  ADS  Google Scholar 

  • Hall C.D.: Spinup dynamics of biaxialgyrostats. J. Astronaut. Sci. 43, 263–275 (1995a)

    MathSciNet  Google Scholar 

  • Hall C.D.: Spinup dynamics of gyrostats. J. Guid. Control Dyn. 18, 1177–1183 (1995b)

    Article  MATH  Google Scholar 

  • Hall C.D., Rand R.H.: Spinup dynamics of axial dual-spin spacecraft. J. Guid. Control Dyn. 17, 30–37 (1994)

    Article  Google Scholar 

  • Henrard J., Wauthier P.: A geometric approach to the ideal resonance problem. Celest. Mech. 44, 227–238 (1989)

    ADS  MathSciNet  Google Scholar 

  • Holmes P.J., Marsden J.E.: Horseshoes and Arnold diffusion for Hamiltonian systems on Lie groups. Indiana Univ. Math. J. 32, 273–309 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  • Howland R.A.: A note on the application of a generalized canonical approach to non-linear Hamiltonian systems. Celest. Mech. 45, 407–412 (1989)

    ADS  MathSciNet  MATH  Google Scholar 

  • Hughes P.C.: Spacecraft Attitude Dynamics. Wiley, New York (1986)

    Google Scholar 

  • Iñarrea M., Lanchares V.: Chaos in the reorientation process of a dual-spin spacecraft with time dependent moments of inertia. Int. J. Bifurcat Chaos 10, 997–1018 (2000)

    MATH  Google Scholar 

  • Koiller J.: A mechanical system with a “wild” horseshoe. J. Math. Phys. 25, 1599–1604 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  • Lanchares, V.: Sistemas dinámicos bajo la acción del grupo SO(3): El caso de un Hamiltoniano cuadrático. Ph.D. dissertation, University of Zaragoza (in Spanish) (1993)

  • Lanchares V., Elipe A.: Bifurcations in biparametric quadratic potentials. Chaos 5, 367–373 (1995a)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Lanchares V., Elipe A.: Bifurcations in biparametric quadratic potentials II. Chaos 5, 531–535 (1995b)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Lanchares V. et al.: Surfaces of bifurcation in a triparametric quadratic Hamiltonian. Phys. Rev. E 52, 5540–5548 (1995)

    Article  ADS  MathSciNet  Google Scholar 

  • Lanchares V., Iñarrea M., Salas J.P.: Spin rotor stabilization of a dual-spin spacecraft with time dependent moments of inertia. Int. J. Bifurcat. Chaos 8, 609–617 (1998)

    Article  MATH  Google Scholar 

  • Leimanis E.: The General Problem of the Motion of Coupled Rigid Bodies About a Fixed Point. Springer Verlag, Berlin (1965)

    MATH  Google Scholar 

  • Miller B.R., Coppola V.T.: Synchronization of perturbed non-linear Hamiltonians. Celest. Mech. Dyn. Astron. 55, 331–350 (1993)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Poinsot L.: Théorie nouvelle de la rotation des corps. J. Math. Pures Appl. 16, 289–336 (1851)

    Google Scholar 

  • Vera J.A., Vigueras A.: Hamiltonian dynamics of a gyrostat in the n-body problem: relative equilibria. Celest. Mech. Dyn. Astron. 94, 289–315 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Volterra V.: Sur la théorie des variations des latitudes. Acta Math. 22, 201–358 (1899)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Grupo de Mecánica Espacial and IUMA, Universidad de Zaragoza, 50009, Zaragoza, Spain

    Antonio Elipe

  2. Department of Mathematics and Computation, Universidad de la Rioja, 26004, Logroño, Spain

    Víctor Lanchares

Authors
  1. Antonio Elipe
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Víctor Lanchares
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Antonio Elipe.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Elipe, A., Lanchares, V. Exact solution of a triaxial gyrostat with one rotor. Celest Mech Dyn Astr 101, 49–68 (2008). https://doi.org/10.1007/s10569-008-9129-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10569-008-9129-6

Keywords

Search

Navigation