Skip to main content
SpringerLink
Log in

Dynamics of a particle in a gravitational field of a homogeneous annulus disk

  • Original Article
  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

Abstract

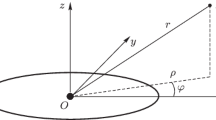
We formulate the problem of an infinitesimal particle moving in the space under the influence of the gravitational force induced by a homogeneous annulus disk fixed on a plane. We compute using different coordinates and in terms of an elliptic integral the potential associated to this problem. Also we study the symmetries of the associated potential. After that, we look at the dynamics in some particular cases, namely: in the line perpendicular to the plane that contains the annulus disk and passes through the center of the ring and on the plane that contains the massive annulus.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Alberti, A.: Dinâmica de uma partícula no potencial de um fio circular homogêneo. Master thesis, Departamento de Matemática—UFPE (2003)

  • Arnold V.I. (1978). Mathematical Methods of Classical Mechanics. Springer, New York

    MATH  Google Scholar 

  • Azevêdo, C., Cabral, H., Ontaneda, P.: On the Fixed Homogeneous Circle Problem. ArXiv: math.DS/0307329v5 (2005)

  • Belbruno E., Llibre J., Ollé M. (1994). On the families of periodic orbits which bifurcate from the circular Sitnikov motions. Celest. Mech. Dynam. Astronom. 60: 99–129

    Article  MATH  ADS  Google Scholar 

  • Broucke R.A., Elipe A. (2005). The Dynamics of Orbits in a Potential Field of a solid Circular Ring. Regular Chaotic Dynam 10(2): 129–143

    Article  MATH  MathSciNet  Google Scholar 

  • Byrd P.F., Friedman M.D. (1954). Handbook of Elliptic Integrals for Engineers and Physicists. Springer Verlag, Berlin, 355

    MATH  Google Scholar 

  • Elipe A., Riaguas A., Lara M. (1999). Periodic orbits around a massive straight segment. Celest. Mech. Dynam. Astronom 73: 169–178

    Article  MATH  ADS  MathSciNet  Google Scholar 

  • Elipe A., Riaguas A. (2003). Nonlinear stability under a logarithmic gravity field. Intern. Math. J. 3(4): 435–453

    MathSciNet  Google Scholar 

  • Elipe A., Lara M. (2003). A simple model for the chaotic motion around (433) Eros. J. Astron. Sci. 51(4): 391–404

    MathSciNet  Google Scholar 

  • Kellog O.D. (1929). Fundations of the Potential Theory. Dover Publications, Inc., New York

    Google Scholar 

  • Lass H., Blitzer L. (1983). The gravitational potential due to uniform disk and rings. Celest. Mech. 30: 225–228

    Article  MATH  ADS  MathSciNet  Google Scholar 

  • MacMillan W.D. (1958). The Theory of the Potential. Dover Publications, Inc., New York

    MATH  Google Scholar 

  • Vidal, C., Alberti, A.: Periodic solutions of a particle in a potential field of a planar massive annulus. Preprint (2006)

Download references

Author information

Authors and Affiliations

  1. Departamento de Matemática, Universidade Federal de Pernambuco, Av. Prof. Luiz Freire, s/n, Cidade Universitária, Recife-Pe, Brasil

    Angelo Alberti

  2. Departamento de Matemática, Facultad de Ciencias, Universidad del Bio Bio, Casilla 5-C, Concepción, VIII-Región, Chile

    Claudio Vidal

Authors
  1. Angelo Alberti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Claudio Vidal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Claudio Vidal.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Alberti, A., Vidal, C. Dynamics of a particle in a gravitational field of a homogeneous annulus disk. Celestial Mech Dyn Astr 98, 75–93 (2007). https://doi.org/10.1007/s10569-007-9071-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10569-007-9071-z

Keywords

Mathematics Subject Classifications

Search

Navigation