Continuity and stability of families of figure eight orbits with finite angular momentum

Abstract

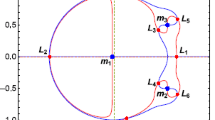
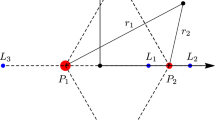
Numerical solutions are presented for a family of three dimensional periodic orbits with three equal masses which connects the classical circular orbit of Lagrange with the figure eight orbit discovered by C. Moore [Moore, C.: Phys. Rev. Lett. 70, 3675–3679 (1993); Chenciner, A., Montgomery, R.: Ann. Math. 152, 881–901 (2000)]. Each member of this family is an orbit with finite angular momentum that is periodic in a frame which rotates with frequency Ω around the horizontal symmetry axis of the figure eight orbit. Numerical solutions for figure eight shaped orbits with finite angular momentum were first reported in [Nauenberg, M.: Phys. Lett. 292, 93–99 (2001)], and mathematical proofs for the existence of such orbits were given in [Marchal, C.: Celest. Mech. Dyn. Astron. 78, 279–298 (2001)], and more recently in [Chenciner, A. et al.: Nonlinearity 18, 1407–1424 (2005)] where also some numerical solutions have been presented. Numerical evidence is given here that the family of such orbits is a continuous function of the rotation frequency Ω which varies between Ω = 0, for the planar figure eight orbit with intrinsic frequency ω, and Ω = ω for the circular Lagrange orbit. Similar numerical solutions are also found for n > 3 equal masses, where n is an odd integer, and an illustration is given for n = 21. Finite angular momentum orbits were also obtained numerically for rotations along the two other symmetry axis of the figure eight orbit [Nauenberg, M.: Phys. Lett. 292, 93–99 (2001)], and some new results are given here. A preliminary non-linear stability analysis of these orbits is given numerically, and some examples are given of nearby stable orbits which bifurcate from these families.