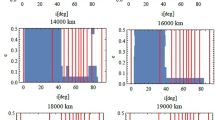
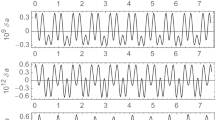
Abstract
This paper presents an analytic solution of the equations of motion of an artificial satellite, obtained using non singular elements for eccentricity. The satellite is under the influence of the gravity field of a central body, expanded in spherical harmonics up to an arbitrary degree and order. We discuss in details the solution we give for the components of the eccentricity vector. For each element, we have divided the Lagrange equations into two parts: the first part is integrated exactly, and the second part is integrated with a perturbation method. The complete solution is the sum of the so-called “main” solution and of the so-called “complementary” solution. To test the accuracy of our method, we compare it to numerical integration and to the method developed in Kaula (Theory of Satellite Geodesy, Blaisdell publ. Co., New York. 1966), expressed in classical orbital elements. For eccentricities which are not very small, the two analytical methods are almost equivalent. For low eccentricities, our method is much more accurate.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
G.E. Cook (1966) ArticleTitlePerturbations of near-circular orbits by the Earth’s gravitational potential Planet. Space Sci. 14 433–444 Occurrence Handle1966P&SS...14..433C
Deleflie F., Métris G., Exertier P. (2006). Long-period variations of the eccentricity vector valid also for near-circular orbits around a non-spherical body, Celest. Mech. Dynam. Astron., this issue.
Demailly J.-P. (1996). Analyse numérique et équations différentielles, EDP Sciences.
P. Exertier (1990) ArticleTitlePrecise determination of mean orbital elements from osculating elements, by semi-analytical filtering Manuscripta Geodaetica 15 115–123
G.E.O. Giacaglia (1977) ArticleTitleThe equations of motion of an artificial satellite in non singular variables Celest. Mech. 15 191–215 Occurrence Handle1977CeMec..15..191G Occurrence Handle0381.70035
W.M. Kaula (1966) Theory of Satellite Geodesy Blaisdell publ. Co. New York
F.G. Lemoine S.C. Kenyon J.K. Factor R.G. Trimmer N.K. Pavlis D.S. Chinn C.M. Cox S.M. Klosko S.B. Luthcke M.H. Torrence Y.M. Wang R.G. Williamson E.C. Pavlis R.H. Rapp T.R. Olson (1998) The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96 Goddard Space Flight Center Greenbelt MD
C.D. Murray S.F. Dermott (1999) Solar System Dynamics Cambridge University Press Cambridge
P.E. Nacozy S.S. Dallas (1977) ArticleTitleThe geopotential in non singular orbital elements Celest. Mech. 15 453–466 Occurrence Handle1977CeMec..15..453N Occurrence Handle57 #2457
Tisserand F. 1890, Traité de Mécanique Céleste, Gauthiers Villards, reprinted. 1960–1962.
E. Wnuk I. Wytrzyszczak (1988) ArticleTitleThe inclination function in terms of non singular Celest. Mech. 42 251–261 Occurrence Handle1988CeMec..42..251W
E. Wnuk (1999) ArticleTitleRecent progress in analytical orbit theories Adv. Space Res. 23 IssueID4 677–687 Occurrence Handle1999AdSpR..23..677W
I. Wytrzyszczak (1986) ArticleTitleNon singular elements in description of the motion of small eccentricity and inclination satellites Celest. Mech. 38 101–109 Occurrence Handle1986CeMec..38..101W Occurrence Handle0627.70025
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Deleflie, F., Métris, G. & Exertier, P. An Analytical Solution of the Lagrange Equations Valid also for Very Low Eccentricities: Influence of a Central Potential. Celestial Mech Dyn Astr 94, 105–134 (2006). https://doi.org/10.1007/s10569-005-1473-1
Received:
Revised:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s10569-005-1473-1