Abstract
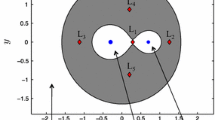
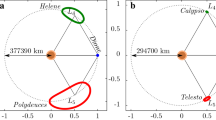
The stability of co-orbital motions is investigated in such exoplanetary systems, where the only known giant planet either moves fully in the habitable zone, or leaves it for some part of its orbit. If the regions around the triangular Lagrangian points are stable, they are possible places for smaller Trojan-like planets. We have determined the nonlinear stability regions around the Lagrangian point L4 of nine exoplanetary systems in the model of the elliptic restricted three-body problem by using the method of the relative Lyapunov indicators. According to our results, all systems could possess small Trojan-like planets. Several features of the stability regions are also discussed. Finally, the size of the stability region around L4 in the elliptic restricted three-body problem is determined as a function of the mass parameter and eccentricity.
Similar content being viewed by others
References
D. B. Caton S. A. Davis K. A. Kluttz R. J. Stamilio K. D. Wohlman (2001) BAAS 33 890
S. A. Davis D. B. Caton K. A. Kluttz K. D. Wohlman R. J. Stamilio K. B. Hix (2001) BAAS 33 1303
R. Dvorak E. Pilat-Lohinger R. Schwarz F. Freistetter (2004) Astron. Astrophys. 426 L37–L40 Occurrence Handle10.1051/0004-6361:200400075
J. Györgyey (1985) Celest. Mech. 36 281 Occurrence Handle10.1007/BF01230741
G. Laughlin J. E. Chambers (2002) Astron. J. 124 592 Occurrence Handle10.1086/341173
E. Lohinger R. Dvorak (1993) Astron. Astrophys. 280 683
M. Nauenberg (2002) Astron J. 124 2332 Occurrence Handle10.1086/342934
G. S. Novak (2002) BAAS 34 939
K. Menou S. Tabachnik (2003) ApJ 583 473 Occurrence Handle10.1086/345359
F. Namouni C. D. Murray (2000) Celest Mech. Dynam. Astron. 76 131 Occurrence Handle10.1023/A:1008385726569
Zs. Sándor B. Érdi C. Efthymiopoulos (2000) Celest. Mech. Dynam. Astron. 78 113 Occurrence Handle10.1023/A:1011112228708
Zs. Sándor B. Érdi C. D. Murray (2002) Celest Mech. Dynam. Astron. 84 355 Occurrence Handle10.1023/A:1021180927001
Zs. Sándor B. Érdi (2003) Celest Mech. Dynam. Astron. 86 301 Occurrence Handle10.1023/A:1024552601635
Zs. Sándor B. Érdi A. Széll B. Funk (2004) Celest Mech. Dynam. Astron. 90 127 Occurrence Handle10.1007/s10569-004-8129-4
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Érdi, B., Sándor, Z. Stability of Co-Orbital Motion in Exoplanetary Systems. Celestial Mech Dyn Astr 92, 113–121 (2005). https://doi.org/10.1007/s10569-004-3114-5
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s10569-004-3114-5