Abstract
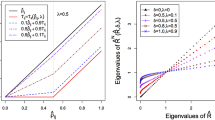
We analyze the consistency of stable estimates of a correlation matrix of observations at their static and dynamic regularization. We prove the advantage of the dynamic regularization method with the optimal parameter in the context of resolving the contradiction “computational stability–consistency” of sample estimates of a correlation matrix of observations. We obtain the algorithm for computation of the optimal parameter of dynamic regularization that do not use predicted data and do not require additional computational costs.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
W. D. Wirth, Radar Techniques Using Array Antennas, The Institution of Engineering and Technology, London (2013).
D. I. Lekhovytskiy, “To the theory of adaptive signal processing in systems with centrally symmetric receive channels,” EURASIP J. Adv. Signal Process, Article number 33 (2016). https://doi.org/https://doi.org/10.1186/s13634-016-0329-z.
D. I. Lekhovitskiy, Yu. I. Abramovich, G. A. Zhuga, and D. S. Rachkov, “Band-diagonal regularization of ML estimates of Gaussian interference correlation matrices in algorithms of antenna arrays adaptation,” Prikladnaya Radioelektronika, Vol. 9, No. 1, 107–121 (2010).
Yu. I. Abramovich, N. K. Spencer, and B. A. Johnson, “Band-inverse TVAR covariance matrix estimation for adaptive detection,” IEEE Trans. on Aerospace and Electronic Systems, Vol. 46, No. 1, 375–396 (2010). https://doi.org/https://doi.org/10.1109/TAES.2010.5417169.
O. P. Cheremisin, “The efficiency of adaptive algorithm with regularization of sample correlation matrix,” Radiotekh. Elektron., Vol. 27, No. 10, 1933–1942 (1982).
A. N. Tikhonov, A. V. Goncharsky, V. V. Stepanov, and A. G. Yagola, Numerical Methods for the Solution of Ill-Posed Problems [in Russian], Nauka, Moscow (1990).
Yu. E. Voskoboinikov and A. A. Mitsel’, Modern Problems of Applied Mathematics, Part 1, Lecture Course [in Russian], Tomskiy Gos. Un-t Sistem Upravleniya i Radioelektroniki (TUSUR), Tomsk (2015).
Yu. S. Osipov, F. P. Vasiliev, and M. M. Potapov, Bases of the Dynamical Regularization Method [in Russian], Izd-vo MGU, Moscow (1999).
V. Skachkov, V. Chepkyi, H. Bratchenko, H. Tkachuk, and N. Kazakova, “Development of the method for dynamic regularization of selected estimates in the correlation matrices of observations,” Eastern-European J. of Enterprise Technologies, Vol. 6, No. 4 (90), 11–18 (2017). https://doi.org/https://doi.org/10.15587/1729-4061.2017.119264.
V. Skachkov, V. Chepkyi, A. Efimchikov, O. Korkin, and A. Dudush “Dynamic regularization parameter optimization of a sample estimate of the correlation matrix of observations by the criterion “computational stability–consistency,” in: Proc. 2019 IEEE 2nd Ukraine Conference on Electrical and Computer Engineering (UKRCON) (Lviv, Ukraine, 2–6 July, 2019), IEEE (2019), pp. 18–23. DOI: https://doi.org/10.1109/UKRCON.2019.8879946.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Kibernetyka ta Systemnyi Analiz, No. 1, January–February, 2021, pp. 94–103.
Rights and permissions
About this article
Cite this article
Skachkov, V.V., Chepkii, V.V., Yefymchykov, O.M. et al. Solving the Problem of Forming Stable and Consistent Estimates of a Correlation Matrix of Observations Using the Method of Dynamic Regularization. Cybern Syst Anal 57, 82–90 (2021). https://doi.org/10.1007/s10559-021-00331-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10559-021-00331-3