Skip to main content
SpringerLink
Log in

Calculation of Bulk Materials Mixing Process

  • RESEARCH, DESIGN, NUMERICAL ANALYSES, AND OPERATING EXPERIENCE
  • PROCESSES AND EQUIPMENT OF CHEMICAL AND OIL-AND-GAS TECHNOLOGIES
  • Published:
Chemical and Petroleum Engineering Aims and scope

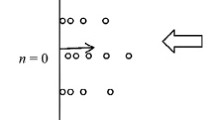
The process of mixing of a diffusing powdery material adjoining an absorbing wall moving in a specific manner is investigated. An entropy method based on statistical approach to the mixing process modeling problem is used as the mathematical apparatus. Given the statistical nature of the investigated phenomenon, an expression based on the postulates of the probability theory is obtained for the key process efficiency parameter (inhomogeneity coefficient) as a function of the parameters of this process. A method for determining the macrodiffusion coefficient that characterizes the particles mixing process intensity is proposed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.

Similar content being viewed by others

References

  1. V. V. Kafarov, Cybernetic Methods in Chemistry and Chemical Engineering [in Russian], Khimiya, Moscow (1985).

    Google Scholar 

  2. L. T. Fan, Y. M. Chen, and F. S. Lai, “Recent developments in solids mixing,” Powder Technology, 61, 255–287 (1990).

    Article  CAS  Google Scholar 

  3. E. A. Barantseva, V. E. Mizonov, S. V. Fedosov, and Yu. V. Khoklova, “A mathematical model of kinetics of blade mixing of bulk materials,” Stroitel. Mater., No. 2, 12–13 (2008).

  4. E. A. Barantseva, V. E. Mizonov, and Yu. V. Khoklova, “Distribution of time of bulk material particles residence in batch blade mixer,” Khim. Prom. Segodnya, No. 3, 50–53 (2009).

  5. Y. Naumenko, “Modeling a flow pattern of the granular fill in the cross section of a rotating chamber,” Eastern-European Journal of Enterprise Technologies, 5, No. 1 (89), 59–69 (2017).

  6. S. N. Cherpitskii, M. Y. Tirshis, L. V. Korolev, and A. V. Kapranova, “An investigation of the process of mixing of bulk materials in a drum-blade mixer,” Khim. Neftegaz. Mashinostr., No. 1, 3–6 (2020).

  7. C. Gardiner, Stochastic Methods in Natural Sciences [Russian translation], Mir, Moscow (1986).

    Google Scholar 

  8. N. A. Fuchs, Mechanics of Aerosols [in Russian], Izd. Akad. Nauk SSSR, Moscow (1955).

    Google Scholar 

  9. V. P. Maikov, Entropy Methods of Modeling in Chemical Engineering [in Russian], MIKhM, Moscow (1981).

    Google Scholar 

  10. E. T. Jaynes, “Principle of maximum entropy,” Maximum-Entropy and Bayesian Methods in Applied Statistics, Cambridge University Press, Cambridge (1996).

    Google Scholar 

  11. E. V. Semenov, A. A. Slavyanskii, I. A. Nikitin, et al., “Calculation of finely dispersed powder mixing process,” Khim. Neftegaz. Mashinostr., No. 3, 3–6 (2020).

  12. I. N. Bronshtein and K. A. Semendyaev, A Handbook of Mathematics for Engineers and Students of Higher Technical Educational Institutions [in Russian], Nauka, Moscow (1986).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. K. G. Razumovskii Moscow State University of Technologies and Management (The First Cossack University) [Moskovskii Gosudarstvennyi Universitet Tekhnologii i Upravleniya im. K. G. Razumovskogo (Pervyi Kazachii Universitet)], Moscow, Russia

    E. V. Semenov, A. A. Slavyanskii, I. A. Nikitin, M. V. Klokonos & D. P. Mitroshina

Authors
  1. E. V. Semenov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. A. Slavyanskii
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. I. A. Nikitin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. V. Klokonos
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. D. P. Mitroshina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. V. Semenov.

Additional information

Translated from Khimicheskoe i Neftegazovoe Mashinostroenie, Vol. 56, No. 10, pp. 3–6, October, 2020.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Semenov, E.V., Slavyanskii, A.A., Nikitin, I.A. et al. Calculation of Bulk Materials Mixing Process. Chem Petrol Eng 56, 779–786 (2021). https://doi.org/10.1007/s10556-021-00842-y

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10556-021-00842-y

Keywords

Search

Navigation