A water-oil emulsion is a unstable liquid system (LS) liable to stratification, comprised of drops (globules) of dispersed water with a diameter of 10–1 to 103 microns. The presence of a solvate shell on the globules prevents their coalescence even during spontaneous collision. To reduce the stability of the emulsion and to facilitate the separation of water from it, i.e., to “destroy” the water-oil emulsion, mechanical, thermochemical and electrochemical methods can be used.

The simplest and relatively rarely used mechanical method is gravitational separation in large-capacity vessels, where the oil is left to settle for 1–2 hr. A higher efficiency of emulsion separation is achieved when a centrifugal force field is used.

The method of settling emulsions in a gravity settler is used in the preparation of water for technological and domestic needs, in the treatment of sewage, etc. The process of gravity separation is an important stage in the natural self-purification of natural and artificial reservoirs [1,2,3,4,5,6,7].

In industry, various devices and machines are used for hydromechanical separation of LS. High separation rates are achieved using filtering equipment, and centrifugal devices, such as centrifuges, separators and hydrocyclones, are the most effective [8,9,10,11].

At the same time, despite the large number of calculated correlations proposed to determine the main performance parameters of devices and machines used for separation of LS, there is no single approach to their calculation. In particular, the methodology for calculating the process of separation of insoluble LS in a gravity settler and in a batch centrifuge has not been sufficiently developed.

In order to improve the technological processes of separation of LS, convenient, easy-to-use and reliable methods for calculating hydrodynamic processes are necessary.

Here, an original mathematical apparatus is offered for calculating the process of separation of insoluble LS in conditions of gravitational settling and in a centrifugal force field.

Formulation of the Problem. An emulsion — a disperse system consisting of microscopic liquid droplets (dispersed phase) distributed in another liquid (dispersion medium) — can be arbitrarily treated as a solution within the framework of the adopted terminology. One of the components is almost always water, the other is a substance composed of weakly polar or neutral molecules.

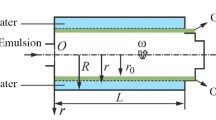
Consider the separation of a solution of two uniformly distributed homogeneous liquids (Fig. 1) — a solvent of density ρ1 and a substance with a density ρ2 dissolved in a given volume of the solvent — in a settler of the height H. For clarity, it is assumed that ρ1 > ρ2.

Fig. 1.
figure 1

Schematic for calculating the process of solution separation in the field of gravity.

Full size image

In a quantitative analysis of the problem posed, it is assumed that the kinetics of the substance dissolved in a liquid volume is similar to the kinetics of a particle suspended in it, whose density is different from the density of the medium. In this case, under the idealized conditions (neglecting viscous effects) it is assumed that sedimentation of a substance in the liquid is only due gravity and Archimedes force, i.e., the buoyant force, acting on it.

The Solution of the Problem. Taking into account the accepted assumption about the nature of the force factors acting on the solute, the d’Alembert principle expression in the projection on the displacement of a given layer, i.e., along the X -axis [1], is taken as the initial kinetic ratio, referring to the unit mass of the selected layer (see Fig. 1) [12]

$$ dv/ dt- g\varDelta \uprho /{\uprho}_2=0, $$

whence, integration taking into account the initial condition v = 0 for t = 0 yields

$$ {v}^2=2g\upzeta x, $$
(1)

where v is the sedimentation rate of the selected layer; g is the acceleration of gravity; x is the current coordinate; ζ is the process control parameter: the effective density of the solution, equal to the specific difference of the phase densities related to the density of the solute,

$$ {\displaystyle \begin{array}{c}\upzeta =\varDelta \uprho /{\uprho}_2,\\ {}\varDelta \uprho ={\uprho}_1-{\uprho}_2,\kern0.5em \varDelta \uprho >0.\end{array}} $$
(2)

Taking into account that in real conditions the sedimentation of the separated layer is of a constrained nature, a correction factor is introduced, then

$$ v=U(c){\left(2g\upzeta x\right)}^{1/2}, $$
(3)

where U(c) = (1− c )3 is a term correcting for the calculated rate of sedimentation, taking into account the condensed character of the dissolved substance [13]; c is the volume concentration of the solute in the liquid volume to be treated.

Since the velocity v = dx/dt, from equation (3) we obtain the differential equation

$$ dx/{x}^{1/2}=U(c){\left(2g\upzeta \right)}^{1/2} dt. $$
(4)

Integrating the left-hand side of expression (4) with respect to x from 0 to H , and the right-hand side — with respect to t from 0 to τ , the equation is obtained for calculating the solution separation process duration period τ (that is, the time interval after which the solute will be completely pushed out upwards by the solvent) in a gravity settler:

$$ \uptau =\frac{1}{{\left(1-c\right)}^3}\sqrt{\frac{2H}{g\upzeta}}. $$

Thus, process duration τ has a parabolic dependence on the height H of the settler, a third-power inverse proportional dependence on the concentration c, and a square root inverse proportional dependence on the effective density ζ .

Calculation of the Solution Separation Process in a Batch Centrifuge

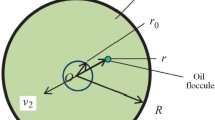
Formulation of the Problem. The test solution is a uniformly mixed LS, a water-oil emulsion model before its treatment in a centrifuge.

We introduce the notation: R, r0 are, respectively, the radius of the rotor and the radius of the free surface of the emulsion layer in the rotor rotating at angular velocity ω ; r is the radial coordinate (Fig. 2). Then the initial kinetic expression of the d’Alembert principle, referred to the unit mass of the selected layer, in the projection on the displacement of the given layer (along the r axis) will take the form

Fig. 2.
figure 2

Schematic for calculating the process of separation of a solution in a centrifugal force field.

Full size image
$$ dv/ dt-{\upomega}^2\upzeta r=0, $$
(6)

where ζ is calculated by equation (2).

The Solution of the Problem. Integrating equation (6) taking into account the initial condition v = 0 for t = 0 , we obtain

$$ {v}^2={\upomega}^2\upzeta {r}^2, $$
(7)

where v is the sedimentation rate of the selected layer.

Since the lighter phase (oil) moves from the periphery towards the axis of rotation of the rotor, then, in light of the correlation (7), the current sedimentation rate of this phase is calculated according to the expression

$$ v=-\upomega \sqrt{\upzeta r}, $$

or, correcting for the constrained nature of the floating of the lighter phase (the dissolved substance — oil),

$$ dv/ dt-\upomega {\left(1-c\right)}^3\sqrt{\upzeta r}, $$

then, after separating the variables and integrating, we get

$$ \underset{R}{\overset{r_0}{\int }}\frac{dr}{r}=-\upomega {\left(1-c\right)}^3\sqrt{\upzeta}{T}_1, $$

where T1 is the solution treatment period.

From equation (8) it follows that

$$ {T}_1=\frac{-1}{\upomega {\left(1-c\right)}^3\sqrt{\upzeta}}\ln \left(\upxi \right), $$

or in dimensionless form

$$ T=\frac{-1}{{\left(1-c\right)}^3\sqrt{\upzeta}}\ln \left(\upxi \right), $$
(9)

where T = T1ω is the dimensionless period of solution treatment; ξ = r0/R is the value of r0 of the free surface of the solution relative to the radius R of the centrifuge rotor (the dimensionless thickness of the solution layer).

Equation (9) is the basis for a quantitative analysis of the process of separation of a water-oil emulsion in a batch centrifuge.

Calculation Results and Discussion

The initial data for calculating the duration τ of the process of separation of the water-oil solution (emulsion) in the sedimentation tank: the volume concentration of oil in solution c = 80, 90%; crude oil density 800, 900 kg/m3; water density ρ1 = 1000 kg/m3. The height of the sedimentation tank was varied in the range of H = 0.1–1.0 m.

The results of the calculation using equation (5) showed (Fig. 3) that the duration τ of the separation process depends significantly on the concentration of oil in the water-oil solution. For example, at a settler height H = 1m and an effective density ζ = 0.1, when crude oil concentration is c = 80 %, the period τ = 2.98min, while when crude oil concentration is c = 90 %, the period τ = 23.81min; for the chosen value of the effective density ζ = 0.2 at an oil concentration c = 80 %, the process duration τ = 2.10min, and for c = 95 %, process duration is τ = 16.84min.

Fig. 3.
figure 3

Duration τ of the process of separation of the liquid system as a function of the height H of the settler for various values of the effective density ζ and the volume concentration c : ζ = 0.1 : 1 – c = 80 %, 2 – c = 90 %; ζ = 0.2 : 3 – c = 80 %, 4 – c = 90 %.

Full size image

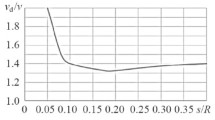
When calculating the duration of the process of separation of a water-oil emulsion in a periodic-action centrifuge, the same initial data were accepted as for a gravity settler. The parameter ξ (dimensionless thickness of the solution layer) varied in the range of 0.05–0.4. The results of the calculations are shown in Fig. 4.

Fig. 4.
figure 4

Dimensionless duration T of the process of separation of the liquid system in a periodic action centrifuge as a function of the dimensionless thickness ξ of the solution layer for various values of the effective density ζ and the volume concentration c : ζ = 0.1 : 1 – c = 80 %, 2 – c = 90 %; ζ = 0.2 : 3 – c = 80 %, 4 – c = 90 %.

Full size image

The dependence of the solution treatment period on the parameters c and ζ , calculated according to equation (9), is similar to the dependence calculated according to equation (5) for the gravity settler. The duration of emulsion treatment increases with decreasing relative thickness of the layer.

At the angular velocity of the centrifuge rotor ω = 400 rad/s and parameter values ζ = 0.1, ξ = 0.4 , c = 90 %, the estimated separation period is 18.2 s.

After the solution treatment period determined by calculation, the target phase (oil) can be evacuated from the centrifuge.

Thus, within the framework of the provisions of theoretical mechanics and hydromechanics, analytical dependences of the rate and period of separation of liquid phases differing in density in a gravity settler and in a periodic action centrifuge were obtained.