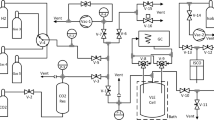
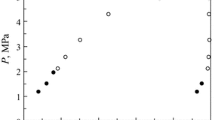
The article deals with the investigation of the ethylene-butane natural gases mixture that is promising for practical application. A unit with a small volume cell created to obtain data on phase equilibria and thermal properties of binary mixtures of little investigated and rare substances using several experimental methods was presented. It is shown that it was possible to use non-standard measuring equipment to obtain sufficiently reliable results in a wide range of temperatures, pressures and compositions. Application of a new method to determine two-component gas mixtures concentration was demonstrated. The method of experimentation was described as well. The experimental results of ethylene–butane mixture thermal properties and vapor-liquid equilibrium that have expanded our knowledge in relation to this two-component natural refrigerant behavior in the low-temperature region and at high dilutions were tabulated. The comparison of the experimental and calculated data showed the possibility of applying the three-parameter cubic equation of state to simulate the thermodynamic properties of the ethylene–butane mixture without using test data of the mixture.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. V. Trotsenko, “Modeling thermodynamic properties of little-researched substances,” Tekh. Gazy, No. 3, 33–39 (2002).
V. A. Naer and A. V. Rozhentsev, “Influence of the mass of the charge of a mixture of refrigerants on the performance characteristics of a low-temperature refrigeration device,” Kholod. Tekhn. Tekhnol., No. 1, 28–39 (2008).
J. C. Rainwater and J. J. Lynch, “A non-linear correlation of high pressure vapor-liquid equilibrium data for ethylene + butane showing inconsistencies in experimental compositions,” Int. J. Thermophys., No. 15, 1231–1239 (1994).
G. D. Efremova and G. A. Sorina, “Phase and volume relations in the ethylene–butane system,” Khim. Prom., No. 6, 503–510 (1960).
B. Williams, PhD Thesis, Vol. 6. Pt. 1, Department of Chemical and Materials Engineering, University of Michigan, Dechema, Michigan, (1949).
Patent 71993 Ukraine, V. N. Valyakin, A. V. Trotsenko, and A. V. Valyakina, IPC G01N 9/02, G01N 27/407, “Gravimetric static method for determining the concentration of two-component gas mixtures,” Byull., No. 15 (2012).
A. V. Trotsenko, “Equation of state of technical gases,” Tekh. Gazy, No. 2, 57–62 (2002).
A. V. Trotsenko and A. V. Valyakina, “Modeling of thermodynamic properties of working fluids on the basis of three-parameter cubic equations of state,” Kholod. Tekhn. Tekhnol., No. 2, 38–42 (2007).
A. V. Trotsenko and A. V. Valyakina, “Generalized algorithm for calculating vapor-liquid equilibrium of pure substances on the basis of cubic equations of state,” Kholod. Tekhn. Tekhnol., No. 1, 80–84 (2011).
A. V. Trotsenko and A. V. Valyakina, “Modeling the processes of gas solubility in liquids for the working fluids of cryogenic and refrigerating machines,” Kholod. Tekhn., No. 8, 24–29 (2016).
Author information
Authors and Affiliations
Additional information
Translated from Khimicheskoe i Neftegazovoe Mashinostroenie, No. 12, pp. 15–21, December, 2017.
Rights and permissions
About this article
Cite this article
Bondarenko, V.L., Valyakina, A.V., Borisenko, A.V. et al. Vapor-Liquid Equilibrium of the Ethylene–Butane Mixture. Chem Petrol Eng 53, 778–787 (2018). https://doi.org/10.1007/s10556-018-0421-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10556-018-0421-3