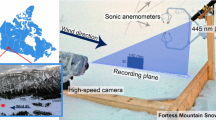
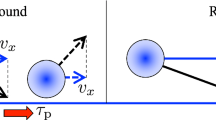
Abstract
Observations of drifting snow on small scales have shown that, in spite of nearly steady winds, the snow mass flux can strongly fluctuate in time and space. Most drifting snow models, however, are not able to describe drifting snow accurately over short time periods or on small spatial scales as they rely on mean flow fields and assume equilibrium saltation. In an attempt to gain understanding of the temporal and spatial variability of drifting snow on small scales, we propose to use a model combination of flow fields from large-eddy simulations (LES) and a Lagrangian stochastic model to calculate snow particle trajectories and so infer snow mass fluxes. Model results show that, if particle aerodynamic entrainment is driven by the shear stress retrieved from the LES, we can obtain a snow mass flux varying in space and time. The obtained fluctuating snow mass flux is qualitatively compared to field and wind-tunnel measurements. The comparison shows that the model results capture the intermittent behaviour of observed drifting snow mass flux yet differences between modelled turbulent structures and those likely to be found in the field complicate quantitative comparisons. Results of a model experiment show that the surface shear-stress distribution and its influence on aerodynamic entrainment appear to be key factors in explaining the intermittency of drifting snow.











Similar content being viewed by others
References
Albertson JD, Parlange MB (1999) Surface length scales and shear stress: implications for land-atmosphere interaction over complex terrain. Water Resour Res 35(7):2121–2132
Alfredsson PH, Johansson AV, Haritonidis JH, Eckelmann H (1988) The fluctuating wall-shear stress and the velocity field in the viscous sublayer. Phys Fluids 31(5):1026–1033
Anderson RS, Haff PK (1991) Wind modification and bed response during saltation of sand in air. Acta Mech Suppl 1:21–51
Araoka K, Maeno N (1981) Dynamical behaviour of snow particles in the saltation layer. In Proceedings of 3rd symposium on polar meteorology and glaciology. Memoirs of Nationa Institute of Polar Research, vol 19, Tokyo, pp 253–263
Baas ACW (2008) Challenges in aeolian geomorphology: investigating aeolian streamers. Geomorphology 93(1–2):3–16
Baas ACW, Sherman DJ (2005) Formation and behavior of aeolian streamers. J Geophys Res 110:F03011
Bagnold RA (1941) The physics of blown sand and desert dunes. Methuen, London, 265 pp
Bou-Zeid E, Meneveau C, Parlange M (2005) A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys Fluids 17(2):025105
Butterfield GR (1998) Transitional behaviour of saltation: wind tunnel observations of unsteady winds. J Arid Environ 39:377–394
Butterfield GR (1999) Application of thermal anemometry and high-frequency measurement of mass flux to aeolian sediment transport research. Geomorphol 29:31–58
Chester S, Meneveau C, Parlange MB (2007) Modeling turbulent flow over fractal trees with renormalized numerical simulation. J Comput Phys 225(1):427–448
Clifton A, Lehning M (2008) Improvement and validation of a snow saltation model using wind tunnel measurements. Earth Surf Process Landf 33:2156–2173
Clifton A, Rüedi J-D, Lehning M (2006) Snow saltation threshold measurements in a drifting snow wind tunnel. J Glaciol 39:585–596
Davidson PA (2004) Turbulence: an introduction for scientists and engineers. Oxford University Press, New York, 657 pp
Deardorff JW (1972) Numerical investigation of neutral and unstable planetary boundary layers. J Atmos Sci 29:91–115
Déry SJ, Yau MK (2001) Simulation of blowing snow in the canadian arctic using a double-moment model. Boundary-Layer Meteorol 99:297–316
Diebold M, Higgins C, Fang J, Bechmann A and Parlange M (2013) Flow over hills: a large-eddy simulation of the bolund case. Boundary-Layer Meteorol 148(1):177–194
Doorschot JJJ, Lehning M (2002) Equilibrium saltation: mass fluxes, aerodynamic entrainment, and dependence on grain properties. Boundary-Layer Meteorol 104(1):111–130
Doorschot JJJ, Lehning M, Vrouwe A (2004) Field measurements of snow-drift threshold and mass fluxes, and related model simulations. Boundary-Layer Meteorol 113(3):347–368
Ellis JT, Sherman DJ, Farrell EJ, Li B (2012) Temporal and spatial variability of aeolian sand transport: implications for field measurements. Aeolian Res 3(4):379–387
Gauer P (1999) Blowing and drifting snow in Alpine Terrain: a physically-based numerical model and related field measurements, Eidg. Institut für Schnee- und Lawinenforschung, Mitteilungen Nr 58, 128 pp
Germano M, Piomelli U, Moin P, Cabot WH (1991) A dynamic subgrid-scale eddy viscosity model. Phys Fluids A 3(7):1760–1765
Gordon M, Biswas S, Taylor PA, Hanesiak J, Albarran-Melzer M, Fargey S (2010) Measurements of drifting and blowing snow at Iqaluit, Nunavut. Canada during the STAR project. Atmos-Ocean 48(2):81–100
Groot Zwaaftink CD, Mott R, Lehning M (2013) Seasonal simulation of drifting snow sublimation in Alpine terrain. Water Resour Res 49:1581–1590
Guala M, Manes C, Clifton A, Lehning M (2008) On the saltation of fresh snow in a wind tunnel: profile characterization and single particle statistics. J Geophys Res 113:F03024
Hardalupas Y, Horender S (2001) Phase Doppler anemometer for measurements of deterministic spray unsteadiness. Part Part Syst Charact 18(4):205–215
Kok JF, Renno NO (2009) A comprehensive numerical model of steady state saltation (COMSALT). J Geophys Res 114:D17204
Lehning M, Löwe H, Ryser M, Raderschall N (2008) Inhomogeneous precipitation distribution and snow transport in steep terrain. Water Resour Res 44(7):W07404
Lenaerts JTM, van den Broeke MR (2012) Modeling drifting snow in Antarctica with a regional climate model: 2. Results. J Geophys Res 117:D05109
Lieberherr G (2010) Modeling snow drift in the turbulent boundary layer. MSc Thesis, EPFL, Lausanne, 36 pp
Lilly DK (1967) The representation of small-scale turbulence in numerical simulation experiments. In Proceedings of the IBM scientific computing symposium on environmental sciences. IBM Form No. 320–1951, White Plains, pp 195–209
Mann GW, Anderson PS, Mobbs SD (2000) Profile measurements of blowing snow at Halley Antarctica. J Geophys Res 105(D19):24491–24508
Moeng CH (1984) A large-eddy simulation model for the study of planetary boundary-layer turbulence. J Atmos Sci 41:2052–2062
Nemoto M, Nishimura K (2004) Numerical simulation of snow saltation and suspension in a turbulent boundary layer. J Geophys Res 109:D18206
Nield JM, Wiggs GFS (2011) The application of terrestrial laser scanning to aeolian saltation cloud measurement and its response to changing surface moisture. Earth Surf Process Landf 36(2):273–278
Nieuwstadt FTM, Brost RA (1986) The decay of convective turbulence. J Atmos Sci 43(6):532–546
Nishimura K, Hunt JCR (2000) Saltation and incipient suspension above a flat particle bed below a turbulent boundary layer. J Fluid Mech 417:77–102
Nishimura K, Nemoto M (2005) Blowing snow at Mizuho station Antarctica. Philos Trans Roy Soc 363(1832):1647–1662
Overney J (2006) Lagrangian stochastic modeling of heavy particle trajectories in atmospheric turbulence. MSc Thesis, EPFL, Lausanne, 55 pp
Pomeroy JW, Marsh P, Gray DM (1997) Application of a distributed blowing snow model to the arctic. Hydrol Proc 11(11):1451–1464
Porté-Agel F, Meneveau C, Parlange MB (2000) A scale-dependent dynamic model for large-eddy simulation: application to a neutral atmospheric boundary layer. J Fluid Mech 415:261–284
Raupach MR (1991) Saltation layers, vegetation canopies and roughness lengths. Acta Mech Suppl 1:83–96
Rice MA, Willetts BB, McEwan IK (1995) An experimental study of multiple grain-size ejecta produced by collisions of saltating grains with a flat bed. Sedimentol 42(4):695–706
Sato T, Higashiura M (1997) Characteristics of blowing snow fluctuation. In: Izumi M et al (eds) Snow engineering: recent advances. Balkema, Rotterdam, 650 pp
Sato T, Uematsu T, Kaneda Y (1997) Application of random walk model to blowing snow. In: Izumi M et al (eds) Snow engineering: recent advances. Balkema, Rotterdam, 650 pp
Schmidt RA (1982) Vertical profiles of wind speed, snow concentration, and humidity in blowing snow. Boundary-Layer Meteorol 23:223–246
Schneiderbauer S, Prokop A (2011) The atmospheric snow-transport model: SnowDrift3D. J Glaciol 57(203):526–542
Shao Y, Li A (1999) Numerical modelling of saltation in the atmospheric surface layer. Boundary-Layer Meteorol 91:199–225
Smagorinsky J (1963) General circulation experiments with the primitive equations: I. The basic experiment. Mon Weather Rev 91(3):99–164
Soldati A (2005) Particles turbulence interactions in boundary layers. Z Angew Math Mech 85(10):683–699
Sterk G, Jacobs AFG, Van Boxel JH (1998) The effect of turbulent flow structures on saltation sand transport in the atmospheric boundary layer. Earth Surface Process Landf 23:877–887
Stout JE, Zobeck TM (1997) Intermittent saltation. Sedimentology 44:959–970
Stull RB (1988) An introduction to boundary layer meteorology. Kluwer Academic Publishers, Dordrecht, 666 pp
Sturm M, Stuefer S (2013) Wind-blown flux rates derived from drifts at arctic snow fences. J Glaciol 59(213):21–34
Sugiura K, Maeno N (2000) Wind-tunnel measurements of restitution coefficients and ejection number of snow particles in drifting snow: Determination of splash functions. Boundary-Layer Meteorol 95(1):123–143
Sugiura K, Nishimura K, Maeno N, Kimura T (1998) Measurements of snow mass flux and transport rate at different particle diameters in drifting snow. Cold Reg Sci Technol 27(2):83–89
Sundsbø PA, Hansen EWM (1997) Modelling and numerical simulation of snow drift around snow fences. In: Izumi M et al (eds) Snow engineering: recent advances. Balkema, Rotterdam
Thomson DJ (1987) Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J Fluid Mech 180:529–556
Tong D, Huang N (2012) Numerical simulation of saltating particles in atmospheric boundary layer over flat bed and sand ripples. J Geophys Res 117:D16205
Vinkovic I (2005) Dispersion et mélange turbulents de particules solides et de gouttelettes par une simulation des grandes échelles et une modélisation stochastique lagrangienne. PhD thesis, Ecole centrale de Lyon
Vinkovic I, Aguirre C, Ayrault M, Simoëns S (2006) Large-eddy simulation of the dispersion of solid particles in a turbulent boundary layer. Boundary-Layer Meteorol 121(2):283–311
Vionnet V, Guyomarc’h G, Martin E, Durand Y, Bellot H, Bel C, Puglièse P (2013) Occurrence of blowing snow events at an alpine site over a 10-year period: observations and modelling. Adv Water Resour 55:53–63
Weil JC, Sullivan PP, Moeng CH (2004) The use of large-eddy simulations in Lagrangian particle dispersion models. J Atmos Sci 61:2877–2887
Wilson JD (2000) Trajectory models for heavy particle in atmospheric turbulence: comparison with observations. J Appl Meteorol 39:1894–1912
Winstral A, Marks D (2002) Simulating wind fields and snow redistribution using terrain-based parameters to model snow accumulation and melt over a semi-arid mountain catchment. Hydrol Proc 16(18):3585–3603
Acknowledgments
We thank Katherine Leonard and Roland Meister for their contribution to the drifting snow measurements at Weissfluhjoch Versuchsfeld. This project is funded by the Swiss National Science Foundation. We thank the reviewers for useful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Groot Zwaaftink, C.D., Diebold, M., Horender, S. et al. Modelling Small-Scale Drifting Snow with a Lagrangian Stochastic Model Based on Large-Eddy Simulations. Boundary-Layer Meteorol 153, 117–139 (2014). https://doi.org/10.1007/s10546-014-9934-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-014-9934-2