Estimation of Roughness Parameters Within Sparse Urban-Like Obstacle Arrays

Abstract

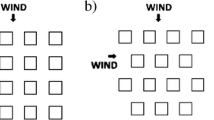
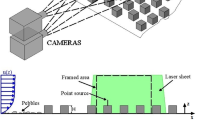
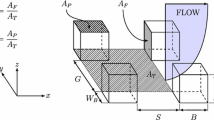
We conduct wind-tunnel experiments on three different uniform roughness arrays composed of sparsely distributed rectangular cylinders for the estimation of surface parameters. Roughness parameters such as the roughness length z ₀ and zero-plane displacement d are extracted using a best-fit approximation of the measured wind velocity. We also perform a large-eddy simulation (LES) to confirm that four sampling points are sufficient to surrogate a space average above the canopy layer of the sparse roughness arrays. We propose a new morphological model from a systematic analysis of experimental data on the arrays. The friction velocity predicted by the proposed model agrees well with the peak value of the measured Reynolds shear stress ${(-\left<\overline{u'w'}\right>)^{0.5}}$. The proposed model is further validated in an additional wind-tunnel experiment conducted on a scaled configuration of a real urban area exposed to four wind directions. The proposed model is found to perform very well particularly in the estimation of the friction velocity, readily leading to a better estimation of turbulence, which is essential for an accurate prediction of pollutant dispersion.