Abstract
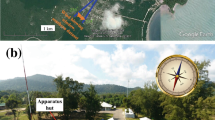
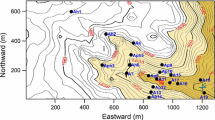
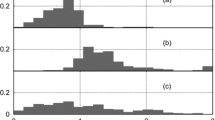
The microstructure of a stably stratified boundary layer, with a significant low-level nocturnal jet, is investigated based on observations from the CASES-99 campaign in Kansas, U.S.A. The reported, high-resolution vertical profiles of the temperature, wind speed, wind direction, pressure, and the turbulent dissipation rate, were collected under nocturnal conditions on October 14, 1999, using the CIRES Tethered Lifting System. Two methods for evaluating instantaneous (1-sec) background profiles are applied to the raw data. The background potential temperature is calculated using the “bubble sort” algorithm to produce a monotonically increasing potential temperature with increasing height. Other scalar quantities are smoothed using a running vertical average. The behaviour of background flow, buoyant overturns, turbulent fluctuations, and their respective histograms are presented. Ratios of the considered length scales and the Ozmidov scale are nearly constant with height, a fact that can be applied in practice for estimating instantaneous profiles of the dissipation rate.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Abramowitz M, Stegun IA (eds) (1972) Handbook of mathematical functions: with formulas, graphs, and mathematical tables. Dover, New York, pp 1044
Balsley BB (2008) The CIRES tethered lifting system: a survey of the system, past results and future capabilities. Acta Geophys 5:21–57. doi:10.2478/s11600-007-0045-z
Balsley BB, Jensen ML, Frehlich R (1998) The use of state-of-the-art kites for profiling the lower atmosphere. Boundary-Layer Meteorol 87:1–25. doi:10.1023/A:1000812511429
Balsley BB, Frehlich RG, Jensen ML, Meillier Y, Muschinski A (2003) Extreme gradients in the nocturnal boundary layer: structure, evolution and potential causes. J Atmos Sci 60:2496–2508. doi:10.1175/1520-0469(2003)060<2496:EGITNB>2.0.CO;2
Balsley BB, Frehlich RG, Jensen ML, Meillier Y (2006) High-resolution in situ profiling through the stable boundary layer: examination of the SBL top in terms of minimum shear, maximum stratification, and turbulence decrease. J Atmos Sci 63:1291–1307. doi:10.1175/JAS3671.1
Balsley BB, Svensson G, Tjernström M (2008) On the scale-dependence of the gradient Richardson number in the residual layer. Boundary-Layer Meteorol 127:57–72. doi:10.1007/s10546-007-9251-0
Banta RM, Newsom RK, Lundquist JK, Pichugina YL, Coulter RL, Mahrt L (2002) Nocturnal low-level jet characteristics over Kansas during cases-99. Boundary-Layer Meteorol 105:221–252. doi:10.1023/A:1019992330866
Beare RJ, MacVean MK (2004) Resolution sensitivity and scaling of large-eddy simulations of the stable boundary layer. Boundary-Layer Meteorol 112:257–281. doi:10.1023/B:BOUN.0000027910.57913.4d
Blumen W, Robert Banta R, Burns SP, Fritts DC, Newsome R, Poulos GS, Sun J (2001) Turbulence statistics of a Kelvin–Helmholtz billow event observed in the night-time boundary layer during the cooperative atmosphere–surface exchange study field program. Dyn Atmos & Oceans 34:189–204. doi:10.1016/S0377-0265(01)00067-7
Caulfield CP, Peltier WR (2000) The anatomy of the mixing transition in homogeneous and stratified free shear layers. J Fluid Mech 413:1–47. doi:10.1017/S0022112000008284
Chimonas H (1999) Steps, waves and turbulence in the stably stratified planetary boundary layer. Boundary-Layer Meteorol 90:397–421. doi:10.1023/A:1001709029773
Crawford WR (1986) A comparison of length scales and decay times of turbulence in stably stratified flows. J Phys Oceanogr 26:1847–1854. doi:10.1175/1520-0485(1986)016<1847:ACOLSA>2.0.CO;2
De Silva IP, Brandt D, Montenegro ALJ, Fernando HJS (1999) Gradient Richardson number measurements in a stratified shear layer. Dyn Atmos & Oceans 30:47–63. doi:10.1016/S0377-0265(99)00015-9
Dillon TM (1982) Vertical overturns: a comparison of Thorpe and Ozmidov length scales. J Geophys Res 87:9601–9613. doi:10.1029/JC087iC12p09601
Ellison TH (1957) Turbulent transport of heat and momentum from an infinite rough plane. J Fluid Mech 2:456–466. doi:10.1017/S0022112057000269
Fritts DC, Rastogi PK (1985) Convective and dynamical instabilities due to buoyancy wave motions in the lower and middle atmosphere: theory and observations. Radio Sci 20:1247–1277. doi:10.1029/RS020i006p01247
Fritts DC, Nappo C, Riggin CM, Balsley BB, Eichinger WE, Newsom RK (2003) Analysis of ducted motions in the stable nocturnal boundary layer during CASES-99. J Atmos Sci 60:2450–2472. doi:10.1175/1520-0469(2003)060<2450:AODMIT>2.0.CO;2
Fernando HJS, Hunt JC, (1996) Some aspects of turbulence and mixing in stably stratified layers. Dyn Atmos & Oceans 23:35–62. doi:10.1016/0377-0265(95)00422-X
Ferron B, Mercier H, Speer K, Gargett A, Polzin K (1998) Mixing in the Romanche fracture zone. J Phys Oceanogr 28:1929–1945. doi:10.1175/1520-0485(1998)028<1929:MITRFZ>2.0.CO;2
Frehlich RY, Meillier M, Jensen L, Balsley BB (2003) Turbulence measurements with the CIRES tethered lifting system during CASES-99: calibration and spectral analysis of temperature and velocity. J Atmos Sci 60:2487–2495. doi:10.1175/1520-0469(2003)060<2487:TMWTCT>2.0.CO;2
Galperin B, Sukoriansky S, Anderson PS (2007) On the critical Richardson number in stably stratified turbulence. Atmos Sci Lett 8:65–69. doi:10.1002/asl.153
Gavrilov NM, Luce H, Crochet M, Dalaudier F, Fukao S (2005) Turbulence parameter estimations from high-resolution balloon temperature measurements of the MUSTI-2000 campaign. Ann Geophys 23: 2401–2413
Howard LN (1961) Note on a paper of John W. Miles. J Fluid Mech 10:509–512. doi:10.1017/S0022112061000317
Itsweire EC, Koseff JR, Briggs DA, Ferziger JH (1993) Turbulent in stratified shear flows: implications for interpreting shear-induced mixing in the ocean. J Phys Oceanogr 28:1508–1522. doi:10.1175/1520-0485(1993)023<1508:TISSFI>2.0.CO;2
Luce H, Fukao S, Dalaudier F, Crochet M (2002) Strong mixing events observed near the tropopause with the MU radar and high-resolution balloon techniques. J Atmos Sci 59:2885–2896. doi:10.1175/1520-0469(2002)059<2885:SMEONT>2.0.CO;2
Mahrt L, Vickers D, (2006) Extremely weak mixing in stable conditions. Boundary-Layer Meteorol 119:19–39. doi:10.1007/s10546-005-9017-5
Miles JW (1961) On the stability of heterogeneous shear flows. J Fluid Mech 10:496–508. doi:10.1017/S0022112061000305
Monin AS, Obukhov AM (1954) Basic laws of turbulence mixing in the surface layer of the atmosphere. Trudy Geof Inst AN SSSR 24: 163–187
Nappo CJ (2002) An introduction to atmospheric buoyancy waves. Academic Press, pp 279
Nappo CJ (2003) Observations of buoyancy wave modulated turbulence in the stable boundary layer during CASES-99 field study. Geophys Res Abstr 5: 01786
Ozmidov PB (1968) Horizontal turbulence and turbulent exchange in the ocean. Publishing House “Science”, Moskow, p 212
Pouols GS, Blumen W, Fritts DC, Lundquist JK, Sun J, Burns SP, Nappo C, Banta R, Newsome R, Cuxart RJ, Terradwllas E, Basley BB, Jensen M (2002) Cases-99: a comprehensive investigation of the stable nocturnal boundary layer. Bull Am Meteorol Soc 4: 576–581
Smyth WD, Moum JN (2000) Length scales of turbulence in stably stratified mixing layers. Phys Fluids 12:1343–1362. doi:10.1063/1.870386
Sorbjan Z (2006) Local structure of turbulence in stably stratified boundary layers. J Atmos Sci 63:1526–1537. doi:10.1175/JAS3704.1
Sorbjan Z (2008a) Local scales of turbulence in the stable boundary layer. Boundary-Layer Meteorol 127:1573–1472. doi:10.1007/s10546-007-9260-z
Sorbjan Z (2008b) Gradient-based similarity in the atmospheric boundary layer. Acta Geophys 5:220–233
Thorpe SA (1977) Turbulence and mixing in a Scottish loch. Philos Trans R Soc Lond A 286:125–181. doi:10.1098/rsta.1977.0112
Winters K, Lombard P, Riley J, D’Asaro EA (1995) Available potential energy and mixing in density-stratified fluids. J Fluid Mech 289:115–128. doi:10.1017/S002211209500125X
Woods JD (19680 Wave-induced shear instability in the summer thermocline. J Fluid Mech 32:791–800. doi:10.1017/S0022112068001035
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Sorbjan, Z., Balsley, B.B. Microstructure of Turbulence in the Stably Stratified Boundary Layer. Boundary-Layer Meteorol 129, 191–210 (2008). https://doi.org/10.1007/s10546-008-9310-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-008-9310-1