Abstract
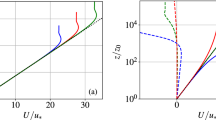
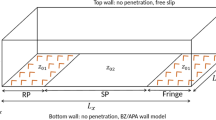
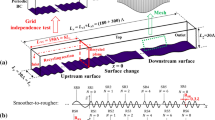
An important parameterization in large-eddy simulations (LESs) of high- Reynolds-number boundary layers, such as the atmospheric boundary layer, is the specification of the surface boundary condition. Typical boundary conditions compute the fluctuating surface shear stress as a function of the resolved (filtered) velocity at the lowest grid points based on similarity theory. However, these approaches are questionable because they use instantaneous (filtered) variables, while similarity theory is only valid for mean quantities. Three of these formulations are implemented in simulations of a neutral atmospheric boundary layer with different aerodynamic surface roughness. Our results show unrealistic influence of surface roughness on the mean profile, variance and spectra of the resolved velocity near the ground, in contradiction of similarity theory. In addition to similarity-based surface boundary conditions, a recent model developed from an a priori experimental study is tested and it is shown to yield more realistic independence of the results to changes in surface roughness. The optimum value of the model parameter found in our simulations matches well the value reported in the a priori wind-tunnel study.
Similar content being viewed by others
References
J. D. Albertson M. B. Parlange (1999) ArticleTitle‘Surface Length Scales and Shear Stress: Implications for Land-Atmosphere Interactions over Complex Terrain’ Water Resources Res. 35 2121–2132 Occurrence Handle10.1029/1999WR900094
W. Cabot P. Moin (2000) ArticleTitle‘Approximate Wall Boundary Conditions in the Large-Eddy Simulation of High Reynolds Number Flow’. Flow, Turbul. Combust. 63 269–291
Grötzbach, G.: 1987, ‘Direct Numerical and Large Eddy Simulations of Turbulent Channel Flows’, in N. P. Cheremisinoff (ed.), Encyclopedia of Fluid Mechanics, Vol. 6, Gulf, pp. 1337–1391.
B. A. Kader (1984) ArticleTitle‘Structure of Anisotropic Velocity and Temperature Fluctuations in a Developed Turbulent Boundary Layer’ Izv. Akad. Nauk SSSR, Meckh. Zhidk. i Gaza 4 47–56
B. A. Kader A. M. Yaglom (1990) ArticleTitle‘Mean Fields and Fluctuation Moments in Unstably Stratified Turbulent Boundary Layers’ J. Fluid Mech. 212 637–662
B. A. Kader A. M. Yaglom (1991) ‘Spectra and Correlation Functions of Surface Layer Atmospheric Turbulence in Unstable Thermal Stratification’ O. Métais M. Lesieur (Eds) Turbulence and Coherent Structures Kluwer Academic Publishers Dordrecht 387–412
G. G. Katul R. C. Chu (1998) ArticleTitle‘A Theoretical and Experimental Investigation of Energy-Containing Scales in the Dynamic Sublayer of Boundary-Layer Flows’ Boundary-Layer Meteorol. 86 279–312 Occurrence Handle10.1023/A:1000657014845
G. G. Katul R. C. Chu M. B. Parlange J. D. Albertson T. A. Ortenburger (1995) ArticleTitle‘Low-Wavenumber Spectral Characteristics of Velocity and Temperature in the Atmospheric Boundary Layer’ J. Geophys. Res. 100 14243–14255 Occurrence Handle10.1029/94JD02616
A. N. Kolmogorov (1941) ArticleTitle‘The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Number’ Dokl. Akad. Nauk S.S.S.R. 30 299–303
P. A. Krogstad R. A. Antonia (1999) ArticleTitle‘Surface Roughness Effects in Turbulent Boundary Layers’ Exp. Fluids 27 450–460
P. A. Krogstad R. A. Antonia L. W. B. Browne (1992) ArticleTitle‘Comparison Between Rough- and Smooth-Wall Turbulent Boundary Layers’ J. Fluid Mech. 245 599–617
I. Marusic G. J. Kunkel F. Porté -Agel (2001) ArticleTitle‘Experimental Study of Wall Boundary Conditions for Large Eddy Simulation’ J. Fluid Mech. 446 309–320
P. J. Mason N. S. Callen (1986) ArticleTitle‘On the Magnitude of the Subgrid-Scale Eddy Coefficient in Large-Eddy Simulations of Turbulent Channel Flow’ J. Fluid Mech. 162 439–462
C. H. Moeng (1984) ArticleTitle‘A Large-Eddy Simulation Model for the Study of Planetary Boundary -Layer Turbulence’ J. Atmos. Sci. 46 2311–2330
A. S. Monin A. M. Obukhov (1954) ArticleTitle‘Basic Laws of Turbulent Mixing in the Ground Layer of the Atmosphere’ Trans. Geophys. Inst. Akad. Nauk. USSR 151 163–187
S.A. Orszag Y.H. Pao (1974) ArticleTitle‘Numerical Computation of Turbulent Shear Flows’ Adv. Geophys. 18A 224–236
A. E. Perry S. M. Henbest M. S. Chong (1986) ArticleTitle‘A Theoretical and Experimental Study of Wall Turbulence’ J. Fluid Mech. 165 163–199
A.E. Perry K.L. Lim S.M. Henbest (1987) ArticleTitle‘An Experimental Study of the Turbulence Structure in Smooth- and Rough-Wall Boundary Layers’ J. Fluid Mech. 177 437–466
U. Piomelli E. Balaras (2002) ArticleTitle‘Wall-Layer Models for Large-Eddy Simulations’ Ann. Rev. Fluid Mech. 34 349–374 Occurrence Handle10.1146/annurev.fluid.34.082901.144919
U. Piomelli J. Ferziger P. Moin (1989) ArticleTitle‘New Approximate Boundary Conditions for Large Eddy Simulations of Wall-Bounded Flows’ Phys. Fluids A 1 IssueID6 1061–1068 Occurrence Handle10.1063/1.857397
S.B. Pope (2000) Turbulent Flows Cambridge University Press U.K. 771
F. Porté -Agel C. Meneveau M. B. Parlange (2000) ArticleTitle‘A Scale-Dependent Dynamic Model for Large-Eddy Simulations: Application to a Neutral Atmospheric Boundary Layer’ J. Fluid Mech. 415 261–284
S. Rajagopalan R. A. Antonia (1979) ArticleTitle‘Some Properties of the Large Structure in a Fully Developed Turbulent Duct Flow’ Phys. Fluids. 22 614–622 Occurrence Handle10.1063/1.862643
S. G. Saddoughi S. V. Veeravalli (1994) ArticleTitle‘Local Isotropy in Turbulent Boundary Layers at high Reynolds Number’ J. Fluid Mech. 268 333–372
H. Schlichting (1979) Boundary-Layer Theory McGraw-Hill New York 817
U. Schumann (1975) ArticleTitle‘Subgrid Scale Model for Finite Difference Simulations of Turbulent Flows in Plane Channels and Annuli’ J. Comp. Phys. 18 376–404
R. B. Stull (1988) An Introduction to Boundary Layer Meteorology Kluwer Academic Publishers Dordrecht 670
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Stoll, R., Porté-agel, F. Effect of Roughness on Surface Boundary Conditions for Large-Eddy Simulation. Boundary-Layer Meteorol 118, 169–187 (2006). https://doi.org/10.1007/s10546-005-4735-2
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10546-005-4735-2