Skip to main content
SpringerLink
Log in

On nonlinear artificial viscosity, discrete maximum principle and hyperbolic conservation laws

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

Abstract

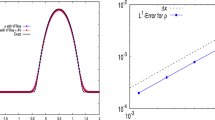
A finite element method for Burgers’ equation is studied. The method is analyzed using techniques from stabilized finite element methods and convergence to entropy solutions is proven under certain hypotheses on the artificial viscosity. In particular we assume that a discrete maximum principle holds. We then construct a nonlinear artificial viscosity that satisfies the assumptions required for convergence and that can be tuned to minimize artificial viscosity away from local extrema.

The theoretical results are exemplified on a numerical example.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. Bertoluzza, The discrete commutator property of approximation spaces, C. R. Acad. Sci., Paris, Sér. I, Math., 329(12) (1999), pp. 1097–1102.

    MATH  MathSciNet  Google Scholar 

  2. E. Burman and A. Ern, Nonlinear diffusion and discrete maximum principle for stabilized Galerkin approximations of the convection–diffusion-reaction equation, Comput. Methods Appl. Mech. Eng., 191(35) (2002), pp. 3833–3855.

    Article  MATH  MathSciNet  Google Scholar 

  3. E. Burman and A. Ern, The discrete maximum principle for stabilized finite element methods, in Numerical Mathematics and Advanced Applications, Springer, Milano, 2003, pp. 557–566.

    Google Scholar 

  4. E. Burman and A. Ern, Stabilized Galerkin approximation of convection–diffusion-reaction equations: discrete maximum principle and convergence, Math. Comput., 74 (2005), pp. 1637–1652 (electronic).

    Article  MATH  MathSciNet  Google Scholar 

  5. E. Burman and A. Ern, Continuous interior penalty hp-finite element methods for advection and advection–diffusion equations, Math. Comput. (2007).

  6. P. G. Ciarlet and P.-A. Raviart, Maximum principle and uniform convergence for the finite element method, Comput. Methods Appl. Mech. Eng., 2 (1973), pp. 17–31.

    Article  MathSciNet  Google Scholar 

  7. B. Cockburn and C.-W. Shu, TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws. II. General framework, Math. Comput., 52 (1989), pp. 411–435.

    Article  MATH  MathSciNet  Google Scholar 

  8. E. Godlewski and P.-A. Raviart, Numerical Approximation of Hyperbolic Systems of Conservation Laws, Applied Mathematical Sciences, vol. 118, Springer, New York, 1996.

    MATH  Google Scholar 

  9. J. Jaffré, C. Johnson, and A. Szepessy, Convergence of the discontinuous Galerkin finite element method for hyperbolic conservation laws, Math. Models Methods Appl. Sci., 5(3) (1995), pp. 367–386.

    Article  MATH  MathSciNet  Google Scholar 

  10. C. Johnson and A. Szepessy, On the convergence of a finite element method for a nonlinear hyperbolic conservation law, Math. Comput., 49 (1987), pp. 427–444.

    Article  MATH  MathSciNet  Google Scholar 

  11. P. G. LeFloch, Hyperbolic systems of conservation laws, Lectures in Mathematics ETH Zürich, Birkhäuser Verlag, Basel, 2002.

  12. R. J. LeVeque, Numerical methods for conservation laws, Lectures in Mathematics ETH Zürich, Birkhäuser Verlag, Basel, 1990.

  13. E. Y. Panov, Uniqueness of the solution of the Cauchy problem for a first-order quasilinear equation with an admissible strictly convex entropy, Mat. Zametki, 55(5) (1994), pp. 116–129, 159.

    MathSciNet  Google Scholar 

  14. J. Smagorinsky, Some historical remarks on the use of nonlinear viscosities, in Large Eddy Simulation of Complex Engineering and Geophysical Flows, Cambridge Univ. Press, New York, 1993, pp. 3–36.

    Google Scholar 

  15. A. Szepessy, Convergence of a shock-capturing streamline diffusion finite element method for a scalar conservation law in two space dimensions, Math. Comput., 53 (1989), pp. 527–545.

    Article  MATH  MathSciNet  Google Scholar 

  16. V. Thomée, Galerkin finite element methods for parabolic problems, Springer Series in Computational Mathematics, vol. 25, Springer, Berlin, 1997.

    MATH  Google Scholar 

  17. J. Von Neumann and R. D. Richtmyer, A method for the numerical calculation of hydrodynamic shocks, J. Appl. Phys., 21 (1950), pp. 232–237.

    Article  MATH  MathSciNet  Google Scholar 

  18. J. Xu and L. Zikatanov, A monotone finite element scheme for convection–diffusion equations, Math. Comput., 68 (1999), pp. 1429–1446.

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Analysis and Scientific Computing, Ecole Polytechnique Fédérale de Lausanne, Station 8, CH-1015, Lausanne, Switzerland

    Erik Burman

Authors
  1. Erik Burman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Erik Burman.

Additional information

AMS subject classification (2000)

65M20, 65M12, 35L65, 76M10

Rights and permissions

Reprints and permissions

About this article

Cite this article

Burman, E. On nonlinear artificial viscosity, discrete maximum principle and hyperbolic conservation laws . Bit Numer Math 47, 715–733 (2007). https://doi.org/10.1007/s10543-007-0147-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10543-007-0147-7

Key words

Search

Navigation