The prior probabilities of phylogenetic trees

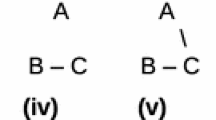
Abstract

Bayesian methods have become among the most popular methods in phylogenetics, but theoretical opposition to this methodology remains. After providing an introduction to Bayesian theory in this context, I attempt to tackle the problem mentioned most often in the literature: the “problem of the priors”—how to assign prior probabilities to tree hypotheses. I first argue that a recent objection—that an appropriate assignment of priors is impossible—is based on a misunderstanding of what ignorance and bias are. I then consider different methods of assigning prior probabilities to trees. I argue that priors need to be derived from an understanding of how distinct taxa have evolved and that the appropriate evolutionary model is captured by the Yule birth–death process. This process leads to a well-known statistical distribution over trees. Though further modifications may be necessary to model more complex aspects of the branching process, they must be modifications to parameters in an underlying Yule model. Ignoring these Yule priors commits a fallacy leading to mistaken inferences both about the trees themselves and about macroevolutionary processes more generally.