1 Introduction

The first AGVs were built in the 1950s and were used for in-house transport by automotive sector plants and by wholesalers. Their present area of application is much wider and includes such applications as hospital logistics and healthcare. The correct operation of AGVs is dependent on the use of a suitable navigation system. This is particularly important in AGVs operating without fixed routes. Some routes are task-specific and they change constantly. Among the basic navigation systems used in such applications is odometry. Odometry assumes the stability of certain values, such as the rolling radius, wheelbase, and a non-occurrence of slippage. Under real-life conditions maintaining the aforementioned assumptions is often not possible. Therefore, odometry is prone to errors that are corrected with additional navigation systems or dedicated calculation algorithms.

The AGV postulated by the authors is an AGV designed for the transport of loads from warehouse buildings to trucks waiting outside. During each individual journey, the AGV may carry loads with a different overall weight. The distribution of each load may vary as well. All of the changes relating to the weight and distribution of the carried loads shall affect the working conditions of the wheels on the pavement surface. The specific operating conditions of the AGV, consisting of frequent changes in the working environment and its configuration, inhibit frequent corrections of positioning by fixed reference points and the use of additional systems, such as GPS or laser navigation. Under such variable operating conditions there is a need for the existence of route sections where odometry is the sole guidance system. After an analysis of the considerations mentioned above, the following solution was proposed. The first step shall be to use data from encoders connected to non-driven rear wheels in navigation. This solution eliminates errors due to wheel slippage which may occur while transferring braking or driving torque. The second step involved an investigation to determine the characteristics of the rolling radiuses under load. This relationship shall allow any necessary adjustments to be made to the calculation algorithm.

The paper is organised as follows. Section 2 lists the literature concerning navigation errors and the determination of the end position. The main causes of these errors and the methods used to alleviate them are described there too. Section 3 formulates the research problem, describes the research object and presents specific work conditions. Section 4 in the first part describes the behavior of the elastic wheel during movement. It presents such parameters related to the movement of the wheel as the rolling radius and a slip. Then it presents the movement equations and the odometry error analysis. In the final part of the section, a new positioning algorithm was proposed containing a block that corrects the effective radiuses of the wheels.

Section 5 presents a description of the experimental research concerning the AGV. A measuring system is presented and requirements concerning research methodology are formulated. Section 6 includes an analysis of the research results. Section 7 features simulation research of AGV movements, with an analysis of the results. Finally, Sect. 8 presents the conclusions which many be drawn from the results of the research.

2 Related work

Various navigation systems are used to guide and position AGVs. Such systems enable vehicle movement from the start point to the end point. Early solutions made use of vehicles which moved along a strictly defined route, set out by an induction, magnetic or optical loop. Due to the inherently low flexibility of such solutions (Martínez-Barberá and Herrero-Pérez 2010) and an ever expanding area of applications, the majority of contemporary AGVs use a guidepath saved in the computer memory of the vehicle (Martinelli 2001). Such systems, based on calculation navigation and odometry, are often referred to as free ranging systems. In odometric systems, positioning is prone to errors. An extensive review with an analysis of such errors can be found in the following studies (Borenstein and Feng 1996; Chong and Kleeman 1997; Martinelli 2002a). There are various errors that affect positioning accuracy. They can be divided into systematic errors and non-systematic errors. Systematic errors are the cumulative errors that are produced while determining the current position of the vehicle in motion (Borenstein and Feng 1996, Kelly 2004b), thus exacerbating the outcome. Depending on the pavement surface type, the share of systematic and non-systematic errors in the positioning accuracy error may vary. Additional calculation errors in navigation may also be produced by the equations of odometry (Epton and Hoover 2012). Such equations describe any trajectory as a series of shorter segments. The accuracy of such an approximation is a function of sampling frequency and vehicle speed. Errors can be corrected using a number of methods. The early work in this area referred to systematic errors and described methods in which position adjustment and system calibration occur after the preset section of the route is covered and the end position error is determined. Among the early methods there is one (Borenstein and Feng 1996) which presents a dedicated calibration technique called UMBmark. This technique was the subject of ongoing modifications. One example is (Lee et al. 2011), where an additional new selection method of the test track for calibration was proposed.

The calibration of non-systematic errors was the research area of authors (Chong and Kleeman 1997) and (Jung et al. 2014). Those studies used the model UMBmark, with further modifications implemented by the authors. The determination of the odometry errors was based on the determination of the AGV end position; this is also the area of interest in studies (Kelly 2004a) and (Martinelli 2002b). The second study uses observables which are measurable quantities related to a given robot motion. The study (Ravikumar et al. 2014) additionally undertakes the determination of AGV wheel load impact on the end position.

Developments in measuring techniques enabled online measurements and therefore the in-motion adjustment of position and calibration of the calculation algorithm. Various measuring techniques may be adopted, as reviewed briefly in the study (Smieszek et al. 2015). Presently, the most common are visual, laser and GPS measurements.

The first studies which refer to online adjustment described the use of ultrasonic sensors (Shoval and Borenstein 1999) and gyroscopes (Kelly 2004b). A further expansion of the range of measuring techniques enabled the adoption of the visual system calibration for error correction. The study (Antonelli et al. 2005) used a video camera erected above the research area. In the study (Chen and Jia 2014) there is an on-board camera, used to determine the AGV position against ceiling-mounted lamps. A visual measuring technique was also used in the analysis of error build-up and a reduction in measurement noise. Descriptions of research studies on AGVs with cameras and inertia sensors are presented in (Knuth and Barooah 2013).

In the literature on online error correction, studies presenting laser range-finders and scanners are well represented. One example of using a laser range-finder is presented in the study (Epton and Hoover 2012). Measurement data enabled error correction calculations to be performed for the vehicle position originally determined by odometry. Also, 2D laser scanners are used to correct odometry errors, as described in studies (Nguyen et al. 2007; Zhao and Chen 2011). Those papers present new algorithms for the positioning (Nguyen et al. 2007) and the detection of lines and curves (Zhao and Chen 2011) in collections of measurement points. The majority of solutions employing additional measurement techniques use complex filtration methods. The study (Smieszek and Dobrzanska 2015) described the application of Kalman filters in the analysis of data from laser range-finders. Filtered data enabled the precise determination of the vehicle position against the reference line and calibration of the navigation system. In the case of vehicles fitted out with two independently driven wheels, with incorrectly estimated values of the rolling radius, the actual movement pattern does not follow a straight line, but rather a curved line with a constant radius. The study (Dobrzanska et al. 2016) assessed the efficiency of various filter types in the determination of the reference line—a curve section. Another example of filter application is the study (Martinelli et al. 2007), assessing the efficiency of two filters the Augmented Kalman Filter and the Observable Filter. The same study also examines the SLAM problem. This problem was described in more detail in papers (Lee and Chung 2010) and (Rodriguez-Losada et al. 2006). The work discussed above assumed that both the wheel and the surface are rigid, that the contact surface is a point and that there is no slippage. Deviations from those assumptions were considered in the final adjustment of position and in the calibration of input data.

In recent years, papers have been published that account for actual movement conditions. Two groups may be isolated based on those studies. One of them deals with the method of slippage detection. The paper (Meng and Bischoff 2004) presents a slippage detection method consisting of a comparison of measurement data from the driven and non-driven wheel. The paper (Ojeda and Borenstein 2006) describes a slippage detection method employing values of route deviation angles determined by gyroscope. Studies (Palacin et al. 2006; Song et al. 2009) present optical methods used in the detection of wheel slip. They compare the circumferential speed of the wheel with the speed of vehicle determined using the optical method. Odometry errors due to slippage may also be determined by comparing data acquired from a group of robots working within a specific workplace. Examples of this are shown in papers (Glas et al. 2015) and (Li et al. 2016), discussing the slippage problem in detail. Slippage may be detected by models describing the kinematics and dynamics of movement (Antonelli and Chiaverini 2007; Gutirrez et al. 2002; Doh et al. 2006; Fernandez et al. 2014) and state observers (Song et al. 2007). The study (Iagnemma and Ward 2008) also accounted for the possibility of the AGV moving under various surface conditions and verifying the model with GPS technology. Papers (Konduri et al. 2014; Lindgren et al. 2002) determine the maximum driving torque transferable by a given wheel. Introducing this value to the guidance algorithm prevents sliding, thus reducing positioning errors.

The second group of studies related to the detection and determination of slippage are concerned with more complex tasks. They employ various models of friction and wheel-soft surface/wheel-hard surface interactions. In the case of hard surfaces this problem is undertaken in the paper (Xiong et al. 2012) and in papers (Tian and Sarkar 2014; Ze-su et al. 2012) employing the “magic formula” developed for cars. In the case of soft deformable surfaces, it uses various models describing surface deformation and wheel-surface interactions. Two areas of interest may be isolated within this group; the first one is all-terrain vehicles, represented in papers (Lindgren et al. 2002; Wu et al. 2011; Ghotbi et al. 2016; Trojnacki and Dabek 2017). The other one is papers discussing the kinematics and dynamics of Moon and Mars rovers. Examples of such papers are (Xiao and Zhang 2016; Shirai and Ishigami 2015).

3 Object of research and its working conditions

3.1 Object of research

A discussion later in the article shall focus on a transport AGV designed for operation in a working environment with variable properties. An example of such a working environment is provided in Fig. 1a in the form of a diagram. The AGV working there, as shown in Fig. 1b moves indoors, inside the building, and outdoors, within the yard where goods are loaded onto trucks. Due to the truck traffic and constant changes to the working environment—from open to enclosed and back—using GPS and visual techniques to determine the position of the AGV may be difficult. In such a variable working environment not too many base points may be determined and used to adjust the current position of the AGV. Therefore, in many sectors of the operating area of the AGV, odometry remains the major navigation system available.

Fig. 1
figure 1

AGV and its workplace environment a diagram, b view of the AGV

Full size image

The object of the research (Fig. 1b) was an automated guided vehicle designed to carry loads, made at the Rzeszow University of Technology. The AGV has three wheels. The front wheel is driven and steered. Non-driven rear wheels are connected to encoders used in the measurement of wheel angle speed. The wheels used in the vehicle (Fig. 1b) had an outer diameter of 200 mm, the width of the band was 50 mm, the permissible load on the rear wheels with a rubber band were 5000 N—rubber hardness 65 ShA. The cargo space of the AGV is suitable for one EUR pallet. Basic technical parameters of the vehicle:

  • Mass of the vehicle ready to work with small batteries is 100 kg,

  • Maximum operating speed of 1 m/s,

  • Two DC motors were used to supply both the drive and steering,

  • The vehicle is able to carry loads of up to 200 kg,

  • Distance beetwen contact points of rear wheels 0.7 m,

  • Wheelbase 1.0 m,

  • Vehicle width 0.8 m,

  • Vehicle length 1.2 m.

Experimental studies were carried out inside a building. The AGV tested was equipped with an on-board computer, data acquisition card NI USB-6343 from National Instruments and suitable control measuring equipment The primary source of information used to determine the position and the direction of vehicle movement were the data read from MHK40 encoders supplied by the Autonics Company. The encoders were connected to the rear wheels.

The front wheel is driven and steered. It is not possible to ensure ideal conditions of wheel-surface contact in the working environment analysed. This refers in particular to the yard, where wheels may slip on coarse or dirty fragments during driving or braking. It was decided that measurement data from the non-driven rear wheels shall be used for positioning purposes. Those wheels were only transferring vertical load, and therefore their sliding due to the loss of traction when accelerating or decelerating could be excluded. In the case analysed, boxes containing goods were manually loaded onto the AGV in the warehouse. Their distribution on the surface of the AGV is often random, as shown in Fig. 1b. Such random distribution leads to a differentiation of the loads on individual wheels. There is a significant change in the load within a single work cycle, comprising AGV transfer from warehouse to truck and back. One half of the route is covered by the AGV with a load and the other half without a load. The cargo may not be exposed to excessive vibrations produced by the coarse pavement surface. The wheels provided suitable vibration damping properties but also demonstrated deformations. Initial experimental studies demonstrated a significant impact of the load on changes in wheel radius. Therefore, in the study presented, it was decided that the problem ought to be investigated more thoroughly, without going into too much detail concerning the physical phenomena occurring within the rubber band of the wheels. During the study, rolling radius characteristics under a load were determined. Computer simulations of motion, employing the above characteristics, demonstrated the potential for influencing the route and the final value of the positioning error.

3.2 The impact of load distribution on wheel load

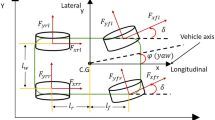
Variable load, in weight and distribution, produces various wheel-surface interactions. The forces acting on the static vehicle are shown in Fig. 2.

Fig. 2
figure 2

Forces acting on the static vehicle: a load scheme, b force distribution

Full size image

The force balance along the Z axis gives

Taking moments about the rear wheels contact point:

$$\begin{aligned} \sum T_{y}=0=m_{L}gx_{L}+mgL_{R}-R_{F}L \end{aligned}$$
(1)

Taking moments about the rear right wheel contact point:

$$\begin{aligned} \sum T_{x}=0=R_{F}\frac{b}{2}+R_{L}b-m_{L}gy_{L}-mg\frac{b}{2} \end{aligned}$$
(2)

Using the equations above and the preset values of vehicle weight m and load weight \(m_{L}\) and the assumed values \(x_{L}\) and \(y_{L}\) pavement surface response, and therefore the loads on individual wheels, were determined. Runs corresponding to various load scenarios are shown in Fig. 3a, b.

Fig. 3
figure 3

Reaction run and load on rear wheels as a function of a shift y, b load weight \(m_{L}\)

Full size image

The above calculations, the results of which are shown in Fig. 3, were made for a static vehicle. In motion, vertical responses are shifted off the wheel contact centre. In variable and curvilinear motion, the vehicle is affected additionally by inertia forces, causing changes in individual wheel loads. Due to slow vehicle speeds and values of longitudinal accelerations and small shifts in reaction force off the wheel centre, additional changes in wheel load are small, and were disregarded in calculations. When analysing diagrams were obtained, it may be pointed out that depending on load position or weight on the vehicle surface, individual wheel loads may change to a large extent. Changes are most pronounced in Fig. 3a, where the effect of shifting fixed weight loads \(m_{L}\) along the axis y, i.e. from one side of the vehicle to another, is shown. In the scenario discussed, wheel load changes from 212 to 866 N i.e. over fourfold. The highest wheel load is observed in the scenario shown in Fig. 3b. Changes in wheel loads are high. Dedicated experimental research and computer simulations are required to explain their impact on vehicle motion and rolling radiuses.

4 Description of AGV motion

4.1 Radius and slip in a deformable wheel

The work described earlier in the Sect. 2 assumed that the vehicle wheel is rigid and that its radius is constant. End position errors are the result of an incorrectly assumed value of the rolling radius and accidental slippage. The final section of the review presents the second group of papers which considers the flexibility of the wheel and its deformations. Such a wheel model shall be the subject of further discussion. Due to the need to damp vibrations produced by coarse surfaces, wheels have flexible band. Band material demonstrates flexibility and vibration absorbing properties. The vertical load on a static wheel leads to its deformation. When the vehicle moves, the forces acting on the wheel cause an additional deformation of its elastic band and in the wheel road contact occur slip zones (Genta 2012). Wheel slip and rolling radius are related to the flexible deformation of the band and with the forces and moment acting on the wheel. In such traffic conditions, the concept of effective radius is used instead of the concept of rolling radius. The slip can be defined in many ways. In many works, the SAE definition (Carlson and Gerdes 2005) is used.

$$\begin{aligned} s=-\frac{v_{x}-\omega r}{v_{x}} \end{aligned}$$
(3)

where \(v_{x}\) is the wheel center speed, \(\omega \)  is the angle speed of the wheel, r is the free radius of the wheel.

Taking into accoun \(v_{\mathrm{x}}=r_{\mathrm{e}}\omega \) we receive

$$\begin{aligned} s=-\frac{r_{e}\omega -r\omega }{r_{e}\omega }=\frac{r}{r_{e}}-1. \end{aligned}$$
(4)

The effective radius in the event of braking varies from r to \(\infty \). Under these conditions, the slip value s ranges from \(-\,1\) to 0.

There are many papers describing the interaction between a wheel with a tyre and the pavement surface. The majority of said papers refer to vehicles. Paper (Hirschberg et al. 2002) describes the wheel-surface interaction model in detail. Papers (Ahn et al. 2011; Carlson and Gerdes 2005; Genta 2012; Miller et al. 2001) present the results of research on car wheel slip.

Fig. 4
figure 4

The course of the longitudinal force as a function of slip for various loads

Full size image

In the range of small slip values s from \(-\,0.025\) to 0.025 the curves for different vertical loads coincide. Such slip values occur under normal traffic conditions on hard surfaces without intense braking and acceleration. The graph shown in Fig. 4 is presented and described in many works (Genta 2012; Hirschberg et al. 2002).

Making use of data included in the papers referred to above and in the paper (Iagnemma and Ward 2008), based on Eqs. (3) and (4), a diagram was developed illustrating changes in the effective radius as a function of the longitudinal load (Fig. 5).

Fig. 5
figure 5

Changes in wheel radius during motion, under the driving force/braking force

Full size image

Depending on the type of motion: driving or braking and the distribution of forces acting on the wheel, the effective radius \(r_{\mathrm{e}}\) used to calculate the distance travelled is changing (Jazar 2008). The effective radius can be defined as the agreed size of the radius of such a rigid wheel, which at the distance \(S_{\mathrm{O}}\) performs the same number of rotations \(n_k\). This describes the relationship:

$$\begin{aligned} S_O=2\pi r_{e} n_{k} \end{aligned}$$
(5)

Thus, the effective radius of the wheel \(r_{e}\) is determined by the formula:

$$\begin{aligned} r_{e}=\frac{S_{\mathrm{O}}}{2\pi n_{k}} \end{aligned}$$
(6)

A theoretical estimation of the effective radius is difficult. A simpler method is to conduct experimental studies aimed at determining the value of the radius, which is the purpose of further research.

4.2 Movement equations

In the majority of traditional odometric solutions we can consider two separate arrangements. In the first, a single wheel is driven and steered. Such a wheel is fitted out with suitable sensors providing information on the distance covered and the wheel turning angle. In the second, two independently driven wheels are used. The second system is often referred to as a differential drive system. In the analysed case, with the front wheel driven and steered, measurement data is provided by the non-driven rear wheels, in order to reduce wheel slip errors. The essence of the solution is shown in Fig. 6.

Fig. 6
figure 6

Adopted odometry coordinate system

Full size image

Current position of AGV O in the base reference system \(X_{0}O_{0}Y_{0}\) (Fig. 6) in iteration k is determined by state vector \((x(k),y(k),\theta (k))\). In iteration \(k+1\) the position is expressed by the equation:

$$\begin{aligned} \begin{aligned}&\left[ \begin{array}{l} x(k+1)\\ y(k+1)\\ \theta (k+1) \end{array} \right] = \left[ \begin{array}{l} x(k)\\ y(k)\\ \theta (k) \end{array} \right] \\&\quad +\left[ \begin{array}{l} {\varDelta }t \cdot v_{\mathrm{O}} \cdot \cos (\theta (k)+{\varDelta }t \cdot \omega (k+1))\\ {\varDelta }t \cdot v_{\mathrm{O}} \cdot \sin (\theta (k)+{\varDelta }t \cdot \omega (k+1))\\ {\varDelta }t \cdot \omega (k+1)) \end{array} \right] \end{aligned} \end{aligned}$$
(7)

Speed values \(v_{\mathrm{O}}\) and \(\omega \) may be determined from Eqs. (8), (9):

$$\begin{aligned} v_{\mathrm{O}}(k+1)= & {} (v_{\mathrm{R}}(k+1)+v_{\mathrm{L}}(k+1))/2 \end{aligned}$$
(8)
$$\begin{aligned} \omega (k+1)= & {} (v_{\mathrm{R}}(k+1)-v_{\mathrm{L}}(k+1))/b \end{aligned}$$
(9)

where \(v_{\mathrm{R}}\) is the right wheel speed, \(v_{\mathrm{L}}\) is the left wheel speed, b is the distance beetwen contact points of driven wheels, \(\omega \) is the angle speed towards O point.

Speed values \(v_{\mathrm{R}}\) and \(v_{\mathrm{L}}\) are expressed by the following equations:

$$\begin{aligned} v_{\mathrm{R}}(k+1)= & {} \omega _{\mathrm{R}}(k+1)\cdot r \end{aligned}$$
(10)
$$\begin{aligned} v_{\mathrm{L}}(k+1)= & {} \omega _{\mathrm{L}}(k+1)\cdot r \end{aligned}$$
(11)

where \(\omega _{\mathrm{R}}\) is the angle speed of right wheel, \(\omega _{\mathrm{L}}\) is the angle speed of left wheel, r is the radius of the wheel.

In the discussion it was assumed that the radius r of all wheels is the same. The following relationships occur between the kinematic values for front wheels and rear wheels:

$$\begin{aligned} v_{\mathrm{A}}= & {} {\dot{\theta }}_{_{\mathrm{A}}}\cdot r \end{aligned}$$
(12)
$$\begin{aligned} \omega= & {} (v_{\mathrm{A}}\sin {\alpha })/l \end{aligned}$$
(13)
$$\begin{aligned} v_{\mathrm{O}}= & {} v_{\mathrm{A}}\cos {\alpha } \end{aligned}$$
(14)

where \({\dot{\theta }}_{_{\mathrm{A}}}\) is the angular velocity of the driven steering wheel, \(\alpha \) is the turning angle of the steering wheel, l is the wheelbase.

Two sources of odometry errors which are considered to be dominant are (Borenstein and Feng 1996):

  • Various wheel radiuses due to production variations and deformations caused by variable wheel load. This error is referred to as radius error \(E_{\mathrm{r}}\):

    $$\begin{aligned} E_{\mathrm{r}}=\frac{r_{\mathrm{R}}}{r_{\mathrm{L}}} \end{aligned}$$
    (15)

    where \(r_{L}\) and \(r_{R}\) are current wheel radiuses.

  • Wheelbase uncertainty—wheelbase is defined as the distance between contact points, in which there is no slip in the curvilinear motion of the two wheels of the moving vehicle and the surface. This error is referred to as wheelbase error \(E_{\mathrm{b}}\):

    $$\begin{aligned} E_{\mathrm{b}}=\frac{b_{\mathrm{a}}}{b_{\mathrm{n}}} \end{aligned}$$
    (16)

    where \(b_{a}\) is the current distance beetwen contact points of driven wheels, \(b_{n}\) is the normal distance beetwen contact points of driven wheels.

The aforementioned errors result in the calculated vehicle trajectory not being identical with the actual trajectory covered by the vehicle.

In the analysed case, the basic values used in the determination of the position of the AGV in odometry are wheel speeds \(v_{\mathrm{L}}\) and \(v_{\mathrm{R}}\). Such speed values are determined based on measurements of angular speed using encoders and rolling radiuses of wheels adopted for calculations. The values of rolling radiuses are not known accurately and they depend on wheel load and wheel slippage at the wheel surface contact area. Changes in the values of rolling radiuses may be the source of both systematic and non-systematic errors.

The position of the \( O (k+1)\) point of the vehicle in the \(k+1\) calculation step, as determined from equations of calculation navigation (7), is burdened with error \({\varDelta } O _{k}\). In order to determine the actual position of the O point, the error \({\varDelta } O _{k}\) needs to be evaluated in each calculation step and added to the theoretical position:

$$\begin{aligned} \widehat{ O }_{k+1}= O _{k+1}+{\varDelta } O _{k} \end{aligned}$$
(17)

where \( O _{k+1}\) is the determined position of the O point, \(\widehat{ O }_{k+1}\) is the actual position of the O point, \({\varDelta } O _{k}\) is the position error.

Error \({\varDelta } O _{k}\) does not have a fixed value, it increases with distance covered. The error propagation principle applies here (Kelly 2004b). In the case of the current and the end position there are three positioning errors: the longitudinal distance error, going along the assumed trajectory \(e_x\), the error perpendicular to the assumed trajectory \(e_y\) and the orientation error \(e_{\theta }\).

Taking into account changes in vehicle load during operation and the resulting deformations and wheel slips, it was decided to modify the algorithm used to calculate the position of the vehicle. The scheme of the modified algorithm is shown in Fig. 7.

Fig. 7
figure 7

Scheme of the modified positioning algorithm

Full size image

In order to eliminate errors and improve the accuracy of position determination, an additional block was introduced. The additional block contains a formula that allows determining the effective radiuses of the wheels as a function of the load. This dependence was developed on the basis of experimental research described in the further part of the work. The current values of effective radiuses are entered into the calculation algorithm using the odometry equations.

5 Research and experiments

5.1 Scope and purpose of research

The theoretical estimation of the impact of load on a slip and rolling radius is a complex and difficult task. There are works (Genta 2012; Tian and Sarkar 2014; Ze-su et al. 2012) where a “magic formula” is used to determine the wheel slip. This method makes it possible to determine such values as the rolling radius and a wheel slip on the basis of available literature data. However, the accuracy of determining these quantities based on literature data is insufficient from the point of view of the proposed calculation procedure shown in Fig. 7. Increasing the accuracy of the estimation requires additional experimental testing. In the considered range of slip changes \(s = \pm 2\)% Fig. 4, it can be seen that the relationship between the slip and load is linear. Taking this fact into account, it is possible to determine directly the dependence of the effective radius on the load without having to refer to a magic formula that requires the estimation of its additional characteristic parameters (Genta 2012). In connection with the above, the main objective of the experimental research described in the further part of this paper is the direct determination of the relationship between the load and the effective radius and the slippage of non-driven wheels. To achieve this goal, it was necessary to conduct a series of tests, collect results and their mathematical development. The dependencies obtained from the research can be directly applied in the calculating effective radiuses block Fig. 7 and concern only one type of wheel being the subject of the research.

The measurements were carried out in the corridor of rigid surface visible in the photo of Fig. 1b. During the tests the length of the distance \(S_{O}\) covered by the vehicle was measured. The value of the distance was measured by a laser range finder and ranged from 37 to 42 m.

Two stages of research can be isolated. Stage 1 was the development and verification of the measurement methodology. This stage consisted of conducting preliminary research aimed at the verification of the measurement system and determination of the requirements concerning vehicle motion. Stage 2 consisted of actual experimental research, during which the relationship between the effective radius and the vertical load was determined. The results of Stage 2 research are presented in Sect. 6.

5.2 Measurement methods

While determining the measurement methodology two variants of vehicle guidance were considered. One of them was manually hauling the AGV along the indicated line. In the other, the AGV was guided automatically along the preset trajectory, routed along the corridor axis. Irrespective of the vehicle guidance method (manual or automatic), it was difficult to obtain accurate rectilinear motion. The paper (Smieszek and Dobrzanska 2015) showed deviations from the assumed route in the automatic guidance scenario. In the automatic guidance scenario, with incorrectly assumed effective radiuses, the vehicle strayed from the route, as shown in Fig. 8a. Imperfections in the steering system caused, in turn, that the vehicle oscillated around the preset line defining the theoretical direction of travel.

The run of these oscillations and the scheme of the measurement are shown in Fig. 8b. Deviation from the preset route, as well as the oscillation observed, resulted in distances travelled by individual AGV wheels, \(S_{L}\) and \(S_{R}\), being different from each other, and also being different from the theoretical value.

Fig. 8
figure 8

Deviations from the preset route a due to incorrectly assumed values of effective radiuses of wheels, b due to imperfections in the control system: \(S_{O}\)—travelled distance, A—amplitude, \(\lambda \)—wavelength

Full size image
Fig. 9
figure 9

Relative error in the function of amplitude A on route at \(S_{O}=40~\hbox {m}\) at wavelength a\(\lambda =40~\hbox {m}\), b\(\lambda =5~\hbox {m}\)

Full size image

In order to determine the effect of deviation from the target track on a measurement size, a series of computer simulations was run. The results are shown in Fig. 9. In cases from Fig. 9a, b it may be observed that the effect of the deviation on the relative error is quite large. To ensure accuracy the deviation had to be minimized. During manual hauling of the AGV along the set out line, the oscillations observed were much smaller than in the automatic guidance scenario. Such a guidance system was used in the main research.

6 Analysis of results

Using the results of experimental research, first the effect of load in changing the wheel radius of the static vehicle was determined. Later, tests were carried out with the vehicle in motion.

During vehicle movement additional deformations occur in the wheel-surface contact area due to the circumferential force, as well as slippage between the elements of the flexible layer and the surface (Genta 2012; Jazar 2008). With constant speed the wheel load is the decisive factor. It is shown in Fig. 10 representing the results of measurements for the left and the right wheel, at constant vehicle speed \(v= 0.5 \, \hbox {m/s}\), under various loads. 60 measurements were taken in the course of the research for the left and the right wheel, spanning over five measurement sessions. Each series of measurements was taken under a different load. Such a presentation of measurement results enables the observation of the dispersion in the results of the individual series. Dispersions of measurement results in individual series are small. Linear regression analysis was adopted in order to find a correlation between the load and the effective radius. Also the 95% confidence interval for linear regressions was determined. Relevant diagrams and data from the regression analysis are shown in Fig. 11a, b. Description of the correlation between the effective radius and the load, obtained using linear regression, is fully sufficient to support further discussions.

Fig. 10
figure 10

Wheel radiuses are arranged in a measurement series for a the left wheel, b the right wheel

Full size image
Fig. 11
figure 11

Linear regression with a determined confidence interval for a the left wheel, b the right wheel

Full size image

7 Simulation research

7.1 Description of the research

As part of the simulation research, it was decided to determine the benefits resulting from an application of the adopted method of determining the position on the basis of the scheme (Fig. 7) and to determine the impact of the dispersion of measurements made in experimental tests on the deviation from the running track set. During the simulation process many variants regarding the mass of transported cargo and its position on the platform were considered. Changing the size of the load mass and the position of its center of gravity influences the load on the wheels and thus their effective radiuses. Calculations carried out in Sect. 3.2, which took into account the impact of the mass of transported cargo and its position, showed that it was possible to change the load in the range from 200 to 1100 N. Using the regression equation from Fig. 11 and selected values of wheel loads from Fig. 3, the effective wheel radius for the considered cases was determined. The results of calculations are presented in Table 1.

The modernized calculation scheme proposed in the Fig. 7 in real motion conditions introduced the values of the effective radius appropriate for a given wheel load to the calculation algorithm. In the original calculation system that does not contain the correcting module, the calculation algorithm, regardless of the mass of the transported load, used in the calculations the constant value of the effective radius assumed for the load \(F_z= 300\,\hbox {N}\). Such a load on the rear wheels occurred in the case of unladen motion. The failure to take into account changes in the effective radius caused, in real motion conditions, a deviation from the set driving path and generated a fault in the final position. In the first part of the simulation process, whose purpose was to determine the benefits of using the modernized position calculation system, trajectories and end positions of the system were compared with the correction (Fig. 7) and without correction. In the case of a modernized system with correction, it was assumed that the way of determining the position is not burdened with errors.

Table 1 Values of the effective radius determined for preset loads
Full size table

The results of calculations of effective radiuses for various loads presented in Table 1 were used in motion simulations where two cases of vehicle load were considered. The first of them assumed that the center of gravity of the transported load lies on the longitudinal symmetry axis of the vehicle \(x_v\) (Fig. 2). In this arrangement, the load on the rear wheels is symmetrical—the same. In the second case, the center of gravity of the transported cargo moved perpendicular to the axis of symmetry \(x_v\) along the y axis. In the final part of the chapter, simulations were carried out during which the influence of uncertainty was investigated—dispersion of experimental results on position error and trajectory of motion. This dispersion was determined based on a \(95\%\) confidence interval.

7.2 Symmetrical load of the rear wheels

In the first case of simulation calculations designed to determine the error of the final position as a result of changing the wheel load, it was assumed that the position of the center of gravity of the transported cargo moves along the longitudinal axis of the vehicle \(x_v\). The load on the right and left wheels is the same. Considering two extreme cases, i.e. an unloaded and fully loaded vehicle, the load of each wheel changes from 300 to 1100 N. Assuming that the effective radius was determined for a non-loaded truck, the maximum ratio of the unladen radius to the fully loaded wheel will be:

for the right wheel

$$\begin{aligned} E_{r}=\frac{r_{eR,F= 300 \, \mathrm{N}}}{r_{eL,F= 1100 \, \mathrm{N}}}=0.98971 \end{aligned}$$
(18)

for the left wheel

$$\begin{aligned} E_{r}=\frac{r_{eR,F= 300 \, \mathrm{N}}}{r_{eL,F= 1100 \, \mathrm{N}}}=0.98825 \end{aligned}$$
(19)

In the motion simulation, it was assumed that the properties of both wheels are identical, and the ratio of the radius of the vehicle wheel unloaded to the radius of the wheel of the loaded vehicle varies between 0.98 and 1.0. During the motion simulation, it was assumed that after going a straight line with a length of 5 m, a curved motion of radius \(R= 3 \, \hbox {m}\) begins. Only one selected point of the vehicle moves along the curve. When the selected vehicle point on the curve reaches the angle of rotation relative to the center of the curve equal to \(\pi /2\), then the selected point of the vehicle starts to move along a straight line with a length of 5 m. The results of the motion simulation and the error of the final position are shown in Fig. 12.

Fig. 12
figure 12

Simulation of the AGV motion with uniformly loaded driving wheels

Full size image

The final error is not big. With a symmetrical wheel load, changes in effective radiuses only affect the distance traveled along a straight line and on the curve. With smaller real effective radiuses, the vehicle will not overcome the assumed straight line and thus will move to the curve earlier. In the course of the curve motion, the angle of rotation equal to \(\pi /2\) will also not be achieved and the end section of the straight line will not be perpendicular to the initial direction of the motion. For error \(E_r=0.98\), the vehicle will cover 4.9 m instead of the 5 m straight section.

7.3 Non-symmetrical load of the rear wheels

In the second part of the simulation process, it was assumed, according to Fig. 3a, that the center of gravity of the load only changes along the y axis, while the x-coordinate is a constant value. The load on the side wheels is asymmetrical and changes to the mass of the same load as the \(y_L\) coordinate of the center of gravity of the load changes. In the calculation algorithm, the values of effective radiuses of left and right wheels for wheel load \(F = 300 \, \hbox {N}\) were assumed as the base. This is the case of an unloaded vehicle. When changing the load position as shown in Fig. 3a, the load on each wheel changes. The range of these changes is the same for both wheels and ranges from 200 to 900 N. In extreme cases, considering the radius ratios for these loads, \(E_r\) will be:

$$\begin{aligned} E_{r}= & {} \frac{r_{eR,F= 200 \, \mathrm{N}}}{r_{eL,F= 900 \, \mathrm{N}}}=0.990766 \end{aligned}$$
(20)
$$\begin{aligned} E_{r}= & {} \frac{r_{eR,F= 900 \, \mathrm{N}}}{r_{eL,F= 200 \, \mathrm{N}}}=1.009821 \end{aligned}$$
(21)

In the further simulations of motion carried out in this part, it was assumed that the ratio of \(E_r\) radiuses varies from 0.99 to 1.01. For this range of changes, a series of simulations was performed to show the deviation from the assumed motion route. In the first place, motion simulations were carried out on a straight line with a length of 15 m. The results of calculations are shown in Fig. 13.

Fig. 13
figure 13

The simulation of AGV motion with non-symmetrical loaded driving wheels in rectilinear motion a the route, b error \(e_{y}\)

Full size image

Then, the motion simulation was carried out on the route consisting of a straight line, a curve and a rectilinear section with the same parameters as in Sect. 7.2. The simulation results are shown in Fig. 14.

Fig. 14
figure 14

Simulation of AGV motion with non-uniformly loaded driving wheels on the assumed route a the route, b error \(e_{x}\)

Full size image

As shown by the results of the simulations presented in Figs. 13 and 14, the change in the position of the center of gravity of the transported load along the y axis perpendicular to the symmetry axis of the vehicle \(x_v\) generates large errors in the trajectory realized and when reaching the final position. This is a very unfavorable way of loading the load platform. At each loading process, it would be necessary to arrange the load so that its center of gravity lies on the axis of symmetry of the vehicle \(x_v\). In real conditions it is impossible. An improvement of accuracy in the implementation of the assumed route requires the use of the correction shown in the diagram (Fig. 7).

7.4 Errors after correction adjustment

In the previously performed simulations it was assumed that the value of the effective radius after correction had no errors. The trajectories of motion with corrected radiuses did not differ from the theoretical course. Therefore, they were used as a pattern for determining errors. In fact, the effective radius determined on the basis of the wheel load is burdened with an error resulting from the dispersion of measurements in experimental research. Within the 95\(\%\) confidence interval shown in Fig. 11a, b one can determine the upper and lower limits of the effective radius for a given load. Thus, the minimum and maximum values of the wheel radiuses for the 95\(\%\) confidence interval can be determined. The results of calculations presenting the ratio of mean value to the minimum and maximum values of radiuses from the 95\(\%\) confidence interval for individual wheels are shown in Fig. 15.

Fig. 15
figure 15

Ratio of extreme values of radius from confidence interval to value from linear regressions a the left wheel b the right wheel

Full size image

In extremely unfavorable cases of load distribution, when one of the wheels takes the maximum value and the second minimal value, error \(E_r\) is in the range from 0.9994 to 1.0006. Assuming the same assumptions regarding the shape of the route as in Fig. 14 and previously determined range of volatility \(E_r\), motion simulations were carried out. As part of these simulations, the route run and the position error were determined as shown in Fig. 16.

Fig. 16
figure 16

Simulation of AGV motion for the value \(E_{r}\) determined from a 95% confidence interval of the linear regression a the route, b the error \(e_{x}\)

Full size image

An introduction of corrected values of rolling wheel radiuses to the calculation algorithm strongly limits the errors of the final position. The maximum \(e_x\) error from Fig. 14 reaching the value of 1.1m was reduced to 0.06 m after the correction was entered (Fig. 16). This error is very small in relation to the error in Fig. 14 and omitting it in the previously performed simulations has no major impact on the considerations conducted.

8 Conclusion

In a vehicle working under fixed, constant load, the correction of systematic errors only required the application of one of the methods described in papers (Borenstein and Feng 1996; Chong and Kleeman 1997; Jung et al. 2014). Such methods enable the determination of wheel effective radiuses upon the final correction of the position. In vehicles working under a variable load, designated for operation under conditions detailed in the article, the previously mentioned methods proved ineffective. Due to workplace configuration, the application of additional measuring techniques is inhibited. Studies and simulations demonstrated a significant impact of load on the effective radiuses of the wheels. After determining the relationship between the effective radius and the wheel load, and determining the vertical load force for the wheel, the determination of the actual value of the effective radius of the wheel shall be possible. Through the implementation of this value in the algorithm reduces the end position error and extends the length of the route which can be covered using the odometry guidance system. This is clearly visible when comparing Figs. 14 and 16. Under actual working conditions a degree of slippage is unavoidable, due to the variability of pavement surfaces. Implementing the corrections in the effective radiuses of wheels will not eliminate the need for additional measuring techniques in the final correction of AGV position. Such a correction may be, however, carried out at longer intervals and at more convenient points of the contemplated workplace operating area of the AGV.