1 Introduction

The turbulent combustion of droplet-laden mixtures plays a key role in several engineering applications (Aggarwal 1998; Lefebvre 1998). Despite its applicability, the physical understanding of droplet-laden mixtures is still incomplete but an improvement in this respect is urgently needed for future designs of lower-emission, higher-efficiency engineering devices and greater control in industrial processes. In the analysis and modelling of turbulent combustion processes, the gradient of the reactive scalar (e.g. reaction progress variable \(c\)) often plays a pivotal role. The magnitude of the gradient of \(c\) (i.e. \(\left| {\nabla c} \right|\)) is commonly known as the Surface Density Function (SDF) (Vervisch et al. 1995; Kollmann and Chen 1998) and, from a modelling perspective, it is important to analyse its statistical behaviour due to its relationship to the Scalar Dissipation Rate (SDR) \(N_{c} = D\left| {\nabla c} \right|^{2}\) (where \(D\) is the diffusivity of \(c\)) (Bray 1980) and generalised Flame Surface Density (FSD) \({{\Sigma }}_{gen} = \overline{{\left| {\nabla c} \right|}}\) (Boger et al. 1998) (where the overbar indicates an appropriate Reynolds averaging/filtering operation). The statistical behaviours of \(\left| {\nabla c} \right|\) and the terms of its transport equation have been analysed extensively for turbulent premixed and stratified flames (Malkeson and Chakraborty 2010a; Dopazo et al. 2015; Dopazo and Cifuentes 2016). However, limited attention has been given to the behaviour of \(\left| {\nabla c} \right|\) in turbulent spray flames (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a). Using Direct Numerical Simulations (DNS) data, Wacks and Chakraborty (2016) analysed the evolution of \(\left| {\nabla c} \right|\) in statistically planar turbulent spray flames for different turbulence intensities, droplet sizes and overall (i.e. fuel in both liquid and gaseous phases is considered) equivalence ratios, whereas Ozel Erol et al. (2019a) examined turbulent spherically expanding flames in droplet-laden mixtures for different turbulence intensities, droplet sizes and overall equivalence ratios. However, the effects of mean shear were absent in the aforementioned canonical configurations (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a) (e.g. statistically planar flames using inflow-outflow with periodic transverse boundaries (Wacks and Chakraborty 2016) or spherically expanding flames (Ozel Erol et al. 2019a)) and, thus, it is worthwhile to analyse a configuration with mean shear, which is typical of many laboratory-scale and industrial burners. A couple of recent analyses (Wang et al. 2017; Sandeep et al. 2018) concentrated on the SDF statistics in a laboratory-scale burner configuration for turbulent premixed flames based on high-fidelity simulations but such an analysis is yet to be conducted for turbulent spray flames. To date, the statistical behaviour of \(\left| {\nabla c} \right|\) and its transport are yet to be assessed for an open turbulent jet spray flame. To address this gap in the existing literature, this study analyses \(\left| {\nabla c} \right|\) and its evolution for an open turbulent jet spray flame using a DNS database (Pillai and Kurose 2018, 2019) corresponding to an experimental Ethanol spray flame (Gounder et al. 2012). The main objectives of the current study are:

  1. (a)

    to identify the statistical behaviour of \(\left| {\nabla c} \right|\) and its evolution for an open turbulent jet spray flame and provide physical explanations for these behaviours.

  2. (b)

    to demonstrate and explain the roles played by flame propagation on the evolution of \(\left| {\nabla c} \right|\) in turbulent spray flames

  3. (c)

    to provide modelling implications of the above findings.

The rest of the paper is organised as follows. The mathematical background and numerical implementation pertaining to this analysis are presented in the next section. This will be followed by the presentation of results and their discussion. The main findings are summarised and conclusions are drawn in the final section of this paper.

2 Mathematical Background and Numerical Implementation

2.1 Considered Case and Computational Configuration

In this study, the DNS configuration corresponds to the experimental investigation of the Ethanol spray EtF3 flame of Gounder et al. (2012). The spray and carrier gas are injected from a central jet nozzle (\(D_{j} = 10.5\;{\text{mm}}\)) with a bulk velocity \(U_{j} = 24\;{\text{m}}\;{\text{s}}^{ - 1}\) surrounded by a coaxial pilot annulus (\(D_{p} = 25\;{\text{mm}}\); \(U_{p} = 11.6\;{\text{m}}\;{\text{s}}^{ - 1}\); \(T_{p} = 2493\;{\text{K}}\)) and an air coflow (\(U_{c} = 4.5\;{\text{m}}\;{\text{s}}^{ - 1}\)). The pilot is composed of the fully burned products of a stoichiometric mixture of 5.08% Acetylene (C2H2), 10.17% Hydrogen (H2) and 84.75% air by volume and provides the heat necessary for the evaporation of the fuel droplets. The flame is stabilised in the shear layer formed between the pilot and inner jet streams. The mass flow rate of liquid Ethanol in the jet is 45 g/min, however, amongst the polydisperse droplet formed by the nebulizer, some droplets evaporate prior to reaching the nozzle exit, giving a partially gaseous fuel at the exit. The Ethanol mass flow rates at the nozzle exit are 14.3 g/min for the gaseous phase and 30.7 g/min for the droplets, resulting in a gaseous equivalence ratio of 0.85.

The DNS data used in this analysis has been reported earlier by Pillai and Kurose (2018, 2019). The simulation has been conducted using the FK3 code (Kitano et al. 2014a, b; Turquand d’Auzay et al. 2019; Ahmed et al. 2020) employing a two-step chemical mechanism. This chemical mechanism accurately captures the equivalence ratio dependence of unstrained laminar burning velocity (Westbrook and Dryer 1981). Although simple chemistry is used in this simulation, the configuration of this study is relatively complex in terms of DNS and took more than 1,100,000 CPU-hours. It is worthwhile to note that the SDF statistics obtained based on DNS with single step chemistry (Chakraborty and Klein 2008; Chakraborty et al. 2013) are found to be in good agreement with the corresponding statistics obtained from detailed chemistry DNS data (Chakraborty et al. 2008, 2013). Therefore, it is expected that the simplification in terms of chemical mechanism should not have any major influence on the conclusions drawn from the current analysis. Moreover, it has been demonstrated elsewhere (Pillai and Kurose 2018, 2019) that the results obtained from DNS are consistent with experimental findings of Gounder et al. (2012). Details of the numerical implementation have been presented in detail elsewhere (Pillai and Kurose 2018, 2019; Turquand d’Auzay et al. 2019) and interested readers are directed towards these studies. Whilst these details will not be repeated here but a brief overview will be provided. The standard conservation equations for mass, momentum, energy and species for reacting flows are solved for the Eulerian gaseous phase. The standard transport equations of position, diameter, momentum, and energy are solved for individual liquid fuel droplets in a Lagrangian framework (Pillai and Kurose 2018, 2019; Kitano et al. 2014a, b; Turquand d’Auzay et al. 2019). Coupling between the Eulerian and Lagrangian phases is achieved by the Particle-Source-In-Cell approach (Pillai and Kurose 2018, 2019; Kitano et al. 2014a, b; Turquand d’Auzay et al. 2019) where particles are modelled as spherical point masses. A polydisperse spray with a diameter distribution matching that of the experiment is injected based on a log-normal distribution with diameters ranging from \(1\;\upmu{\text{m}}\) to \(80\;\upmu{\text{m}}\) (the most likely diameter is \(\sim\,20\;\upmu{\text{m}}\)). Details of the particle diameter distribution considered have been discussed in detail elsewhere and interested readers are directed to Pillai and Kurose (2018) for further information. As this is a dilute flame with an inflow droplet volume fraction of \(\sim5 \times 10^{ - 4}\), the collisions and break-up have been neglected.

A domain of \(94D_{j} \times 49D_{j} \times 49D_{j}\) is used and is discretised by a non-uniform \(1160 \times 400 \times 400\) Cartesian grid. A large stretching is applied in all directions towards the boundaries to form absorbing zones that minimize reflection and contamination of the acoustic field near the jet (Pillai and Kurose 2018, 2019). Due to the coupling strategy between the Eulerian and Lagrangian phases, the minimum cell size must be larger than the droplet size to accurately capture the evaporation process (Pillai and Kurose 2018, 2019). To ensure an appropriate resolution of both the turbulence and the flame structure, the smallest cell size at the nozzle exit is taken to be \(\Delta x = 150\;\upmu{\text{m}}\). Further details on the boundary conditions and mesh can be found in (Pillai and Kurose 2018, 2019; Kitano et al. 2014a, b; Turquand d’Auzay et al. 2019). The turbulence intensity decreases and the integral length scale increases as turbulence decays in the downstream direction. The Kolmogorov length-scale \(\eta_{k}\) increases continuously in the downstream direction from \(\eta_{k} \approx 170\;\upmu{\text{m}}\) (i.e. \(\Delta x/\eta_{k} \approx 1.35\)) at the nozzle lip, and the ratio of grid spacing to the Kolmogoroov length scale throughout the domain remains consistent with the DNS grid requirement recommended by Pope (2000). The turbulent Reynolds number \(Re_{t}\) is in the range of 50–100 in the shear layer of the axial locations considered as discussed in detail in previous studies of this simulation (Pillai and Kurose 2019; Turquand d’Auzay et al. 2019). Additionally, a two-step global chemistry is used as the reaction model, which requires much less spatial resolution in comparison to more detailed chemical mechanisms employed elsewhere. The thermal flame thickness of the corresponding laminar premixed stoichiometric flame is 536 μm. Therefore, the grid resolution is sufficient inside the jet flame region.

2.2 Relevant Mathematical Background

The evaporation of droplets leads to mixture inhomogeneities that can be characterised by the mixture fraction \(\xi\), which can be defined as \(\xi = \left( {\beta - \beta_{O} } \right)/(\beta_{f} - \beta_{O} )\) (Bilger 1980) where \(\beta_{f} = 6.0/W_{{C_{2} H_{6} O}}\), \(\beta_{O} = - Y_{O\infty } /W_{O}\) and \(\beta = 2Y_{C} /W_{C} + 0.5Y_{H} /W_{H} - Y_{O} /W_{O}\) where \(Y_{\alpha }\) and \(W_{\alpha }\) are mass fraction and the molar mass of element \(\alpha\), respectively. A reaction progress variable \(c\) based on the oxidiser mass fraction can be defined, following several previous analyses (Wacks and Chakraborty 2016; Ozel Erol et al. 2018, 2019a, b, c; Fujita et al. 2013; Wacks et al. 2016; Wandel 2013, 2014), as \(c = \left[ {\left( {1 - \xi } \right)Y_{{O_{2} \infty }} - Y_{{O_{2} }} } \right]/\left[ {\left( {1 - \xi } \right)Y_{{O_{2} \infty }} - Y_{{O_{2} }}^{Eq} } \right]\) where \(Y_{{O_{2} }}\) is the oxygen mass fraction, \(Y_{{O_{2} \infty }}\) is the oxygen mass fraction in the pure oxidiser stream and \(Y_{{O_{2} }}^{Eq}\) is the equilibrium oxidiser mass fraction (i.e. \(Y_{{O_{2} }}^{Eq} = f(Y_{{O_{2} }} ,\xi )\)). Furthermore, the definition of \(c\) is consistent with a number of previous studies of turbulent stratified flames where variations in mixture fraction exist (Hélie and Trouvé 1998; Bray et al. 2005; Malkeson and Chakraborty 2010b, c, c, d, f). The transport equation for \(c\) takes the following form (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a):

$$\rho \left( {\partial c/\partial t} \right) + \rho u_{j} \left( {\partial c/\partial x_{j} } \right) = \nabla \cdot \left( {\rho D\nabla c} \right) + \dot{\omega }_{c} + \dot{S}_{ev} + \dot{S}_{c}$$
(1)

where \(D\) is the progress variable diffusivity. The first term on the right-hand-side of Eq. (1) arises due to molecular diffusion, the second term represents the reaction rate, the third term is the source/sink term due to droplet evaporation, and the final term is the cross-scalar dissipation term due to reactant inhomogeneity (Malkeson and Chakraborty 2010a; Wacks and Chakraborty 2016; Ozel Erol et al. 2019a). The definitions of \(\dot{\omega }_{c}\), \(\dot{S}_{ev}\) and \(\dot{S}_{c}\) depend on the local value of \(\xi\). In Eq. (1), \(\dot{\omega }_{c}\) is defined in the following manner (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a):

$$\dot{\omega }_{c} = - \left[ {\xi_{st} \dot{\omega }_{{O_{2} }} } \right]/\left[ {\xi \left( {1 - \xi_{st} } \right)Y_{{O_{2} \infty }} } \right]\;{\text{for}}\;\xi \le \xi_{st}$$
(2i)
$$\dot{\omega }_{c} = - \dot{\omega }_{{O_{2} }} /\left[ {\left( {1 - \xi } \right)Y_{{O_{2} \infty }} } \right] \;\;{\text{for}}\;\;\xi > \xi_{st}$$
(2ii)

where \(\xi_{st} = \left( { - \beta_{O} } \right)/(\beta_{f} - \beta_{O} )\) is the stoichiometric mixture fraction. In Eq. (1), \(\dot{S}_{ev}\) is defined as (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a):

$$\dot{S}_{ev} = \left\{ { - \xi_{st} /\left[ {\xi^{2} \left( {1 - \xi_{st} } \right)Y_{{O_{2} \infty }} } \right]} \right\}\left( {\xi \dot{S}_{O} + \left( {Y_{{O_{2} \infty }} - Y_{{O_{2} }} } \right)\dot{S}_{\xi } } \right)\;{\text{for}}\;\xi \le \xi_{st}$$
(3i)
$$\dot{S}_{ev} = \left\{ { - 1/\left[ {\left( {1 - \xi_{st} } \right)^{2} Y_{{O_{2} \infty }} } \right]} \right\}\left( {\left( {1 - \xi } \right)\dot{S}_{O} + Y_{{O_{2} }} \dot{S}_{\xi } } \right)\;\;{\text{for}}\;\;\xi > \xi_{st}$$
(3ii)

where \(\dot{S}_{\xi } = \left( {\dot{S}_{F} - \dot{S}_{O} /s} \right)/\left( {Y_{F\infty } - Y_{{O_{2} \infty }} /s} \right)\) is the droplet source/sink term in the \({{\upxi }}\) transport equation, \(\dot{S}_{F} = \left( {1 - Y_{F} } \right){{\Gamma }}_{m}\) and \(\dot{S}_{O} = - Y_{{O_{2} }} {{\Gamma }}_{m}\) are the droplet source/sink terms in the fuel and oxygen transport equations, respectively, and \({{\Gamma }}_{m}\) is the source term in the mass conservation equation due to evaporation. In Eq. (1), \(\dot{S}_{c}\) is defined as (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a):

$$\dot{S}_{c} = \left( {2\rho D/\xi } \right)\nabla c \cdot \nabla {{\upxi }} \;\;{\text{for}}\;\;\xi \le \xi_{st}$$
(4i)
$$\dot{S}_{c} = \left\{ { - 2\rho D/\left( {1 - \xi } \right)} \right\}\nabla c \cdot \nabla {{\upxi }}\;\;{\text{for}}\;\;\xi > \xi_{st}$$
(4ii)

The molecular diffusion term in Eq. (1) (i.e. \(\nabla \cdot \left( {\rho D\nabla c} \right) = \vec{N} \cdot \nabla \left( {\rho D\vec{N} \cdot \nabla c} \right) - 2\rho D\kappa_{m} \left| {\nabla c} \right|\)) can be split into its flame normal (i.e. \(\vec{N} \cdot \nabla \left( {\rho D\vec{N} \cdot \nabla c} \right)\)) and tangential \(\left( {{\text{i}}.{\text{e}}. - 2\rho D\kappa_{m} \left| {\nabla c} \right|} \right)\) components (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a; Echekki and Chen 1999) where \(\vec{N} = - \nabla c/\left| {\nabla c} \right|\) is the flame normal vector, \(\kappa_{m} = 0.5\left( {\nabla \cdot \vec{N}} \right)\) is the curvature of a given \(c = c^{*}\) iso-surface.

The transport equation of \(c\) (see Eq. 1) can be rewritten in kinematic form as (Dopazo et al. 2015; Dopazo and Cifuentes 2016):

$$\partial c/\partial t + u_{j} \left( {\partial c/\partial x_{j} } \right) = S_{d} \left| {\nabla c} \right|$$
(5)

where \(S_{d}\) is the displacement speed, which is given by (Ozel Erol et al. 2019a; Wang et al. 2017):

$$S_{d} = \underbrace {{\vec{N} \cdot \nabla \left( {\rho D\vec{N} \cdot \nabla c} \right)/\rho \left| {\nabla {\text{c}}} \right|}}_{{S_{n} }} + \underbrace {\left({ - 2D\kappa_{m} }\right)}_{{S_{t} }} + \underbrace {{\dot{\omega }_{c} /\rho \left| {\nabla {\text{c}}} \right|}}_{{S_{r} }} + \underbrace {{\dot{S}_{ev} /\rho \left| {\nabla {\text{c}}} \right|}}_{{S_{ev} }} + \underbrace {{\dot{S}_{c} /\rho \left| {\nabla {\text{c}}} \right|}}_{{S_{c} }}$$
(6)

The SDF transport equation takes the following form (Dopazo et al. 2015; Dopazo and Cifuentes 2016; Wacks and Chakraborty 2016; Ozel Erol et al. 2019a; Wang et al. 2017):

$$\partial \left| {\nabla c} \right|/\partial t + V_{j} \left( {\partial \left| {\nabla c} \right|/\partial x_{j} } \right) = - \left( {a_{N} + N_{j} \left( {\partial S_{d} /\partial x_{j} } \right)} \right)\left| {\nabla c} \right|$$
(7i)
$$\partial \left| {\nabla c} \right|/\partial t + \partial \left( {V_{j} \left| {\nabla c} \right|} \right)/\partial x_{j} = \left( {a_{T} + 2S_{d} \kappa_{m} } \right)\left| {\nabla c} \right|$$
(7ii)

where \(a_{N} = N_{i} N_{j} \partial u_{i} /\partial x_{j}\) and \(a_{T} = \nabla .\vec{u} - a_{N} = \left( {\delta_{ij} - N_{i} N_{j} } \right)\partial u_{i} /\partial x_{j}\) are the flame normal and tangential strain rates, respectively, \(V_{j} = u_{j} + S_{d} N_{j}\) is the jth component of the flame propagation velocity, \(\nabla .\vec{u}\) is the dilatation rate, \(N_{j} \left( {\partial S_{d} /\partial x_{j} } \right)\) is the normal strain rate induced by flame propagation and \(2S_{d} \kappa_{m}\) is the tangential strain rate due to flame propagation (or curvature stretch rate) (Dopazo et al. 2015; Dopazo and Cifuentes 2016; Candel and Poinsot 1990). Furthermore, it can be shown that (Dopazo et al. 2015; Dopazo and Cifuentes 2016):

$$\left( {1/\Delta x_{n} } \right)\left( {d\Delta x_{n} /dt} \right) = \left( {a_{N} + N_{j} \left( {\partial S_{d} /\partial x_{j} } \right)} \right) = a_{N}^{eff}$$
(8)

where \(\Delta x_{n}\) is the distance between two neighbouring \(c\) iso-surfaces and \(a_{N}^{eff}\) is the effective flame normal strain rate (Dopazo and Cifuentes 2016; Wacks and Chakraborty 2016; Ozel Erol et al. 2019a; Wang et al. 2017; Sandeep et al. 2018). For \((a_{N} + N_{j} (\partial S_{d} /\partial x_{j} )) > 0\), the separation between \(c\) iso-surfaces increases but \(\left| {\nabla c} \right|\) decreases. Moreover, the evolution of an elemental flame surface area \(A\) can be written as (Dopazo and Cifuentes 2016; Candel and Poinsot 1990):

$$\left( {1/A} \right)\left( {dA/dt} \right) = a_{T} + 2S_{d} \kappa_{m} = a_{T}^{eff}$$
(9)

where \(a_{T}^{eff}\) is the effective tangential strain rate (or flame stretch rate) (Dopazo et al. 2015; Dopazo and Cifuentes 2016; Candel and Poinsot 1990). Equations (7)–(9) suggest that the statistical behaviours of \(\nabla .\vec{u}\), \(a_{N}\), \(a_{T}\), \(N_{j} \left( {\partial S_{d} /\partial x_{j} } \right)\) and \(2S_{d} \kappa_{m}\) determine \(\left| {\nabla c} \right|\) and flame area generation in turbulent spray flames, which will be discussed in the next section.

3 Results and Discussion

3.1 General Flame Behaviour and Structure

The instantaneous iso-surface of reaction progress variable \(c = 0.75\) coloured with normalised mixture fraction \(\xi /\xi_{st}\) at \(t_{sim} = 0.024s\) is presented in Fig. 1a, which shows the variations in \(\xi /\xi_{st}\) due to droplet evaporation as well as due to the interaction between the flame, droplets and turbulent velocity field. The instantaneous field of normalised mixture fraction \(\xi /\xi_{st}\) on the central x–y plane is presented in Fig. 1b. It can be noticed in Fig. 1b that the evaporation process occurs in the mixing layer, which increases continuously from the nozzle lip and shows large values of \(\xi\) up to \(\xi /\xi_{st} = 2.0\) at \(x/D_{j} = 15\) and \(\xi /\xi_{st} = 2.5\) at \(x/D_{j} = 20\) before decreasing due to mixing. Around the pockets of high fuel content created by the droplet evaporation (as shown in Fig. 1b), the burning occurs predominantly in a non-premixed mode as the hot fuel does not have the time to fully mix with the surrounding air, and leads to partial-premixing, which is characteristic of spray flames. This trend strengthens further in the downstream direction. The nature of the combustion (e.g. premixed, non-premixed) can be characterised by considering a Flame Index, \(FI\). A modified Flame Index, \(FI\), has previously been proposed by Briones et al. (2006) building upon the work of Yamashita et al. (1996) in the following manner:

$$FI = \frac{1}{2}\frac{{\xi - \xi_{st} }}{{\left| {\xi - \xi_{st} } \right|}}\left( {1 + \frac{{\nabla Y_{{C_{2} H_{6} O}} \cdot \nabla Y_{{O_{2} }} }}{{\left| {\nabla Y_{{C_{2} H_{6} O}} } \right| \cdot \left| {\nabla Y_{{O_{2} }} } \right|}}} \right)$$
(10)

where the modified Flame Index, \(FI\), assumes values between \(- 1\) and \(+ 1.\) A value of \(FI = - 1.0\) indicates a lean premixed mode of combustion, whereas a value of \(FI = 1.0\) indicates a rich premixed mode of combustion and a value of \(FI = 0\) indicates a diffusion flame. Probability density functions of the modified Flame Index, \(FI\), at different reaction progress variable values (i.e. \(c = 0.1\), \(0.3\), \(0.5\), \(0.7\) and \(0.9\)) at \(x/D_{j} = 2\), \(6\) and \(10\) are shown in Fig. 2a–c, respectively. It can be seen from Fig. 2 that close to the nozzle exit (\(x/D_{j} = 2\)) the lean premixed mode of combustion remains dominant but rich premixed combustion becomes more dominant moving towards the burned gas side of the flame as droplets evaporate. However, moving further downstream (i.e. \(x/D_{j} = 6\) and \(10\)), greater contributions of non-premixed mode of combustion can be seen towards the unburned gas side of the flame (i.e. \(c = 0.1\)) due to a greater number of droplets beginning to evaporate far downstream of the jet exit. The non-premixed mode of combustion decreases (i.e. the PDF peak at \(FI = 0\) decreases) with increasing \(c\), as mixing progressively takes place within the flame.

Fig. 1
figure 1

Instantaneous plots at \(t_{sim} = 0.024s\) of a \(c = 0.75\) iso-surface coloured with \(\xi\) / \(\xi_{st}\) and b \(\xi\) / \(\xi_{st}\) at the central x–y plane with the \(c = 0.75\) iso-contour [ ]

Full size image
Fig. 2
figure 2

Probability density functions of the modified Flame Index, \(FI\), for \(c = 0.1\), \(0.3\), \(0.5\), \(0.7\) and \(0.9\), at a \(x = 2D_{j}\), b \(x = 6D_{j}\) and c \(x = 10D_{j}\)

Full size image

The increased probability of finding fuel rich mixtures in the downstream direction, as observed in Fig. 1b and Fig. 2, is reflected in the variations of the mean values of \(\xi\) conditional upon \(c\), which are shown in Fig. 3a at \(x/D_{j} = 2\), \(6\) and \(10\). The locations at \(x/D_{j} = 2\), \(6\) and \(10\) will be considered to analyse the behaviour of \(\left| {\nabla c} \right|\) and its evolution in the current study. Figure 3a indicates that likelihood of obtaining fuel-rich mixture increases towards the burned gas due to droplet evaporation at each of the locations considered, which is also consistent with Fig. 2. It should be noted that there are no occurrences of spontaneous ignition in the upstream shear layer. It was neither found in the simulation (Pillai and Kurose 2018, 2019) or nor was it reported in the experiments by Gounder et al. (2012). The absence of sufficient flammable mixture in the shear layer before a propagating partially-premixed flame is established precludes the possibility of autoignition in this configuration.

Fig. 3
figure 3

Profiles of the mean values of a ξ and b \(\left| {\nabla c} \right| \times \delta_{th,st}\) conditional upon \(c\) at \(x/D_{j} = 2\) [ ], \(6\) [ ] and \(10\) [ ]. In b, [ ] indicates \(\left| {\nabla c} \right| \times \delta_{th,st}\) for the laminar premixed flame

Full size image

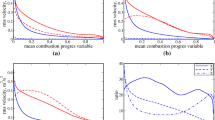
The profiles of the mean values of \(\left| {\nabla c} \right| \times \delta_{th,st}\) (where \(\delta_{th,st}\) is the thermal flame thickness of the stoichiometric mixture) conditional upon \(c\) are shown in Fig. 3b at \(x/D_{j} = 2\), \(6\) and \(10\) as well as for the corresponding stoichiometric laminar unstretched premixed flame, showing that \(\left| {\nabla c} \right| \times \delta_{th,st}\) decreases moving downstream. The inverse of the peak mean value of \(\left| {\nabla c} \right|\) provides a measure of flame thickness and thus Fig. 3b suggests that the flame thickens in the downstream direction. As the characteristic flame thickness increases with increasing \(\xi /\xi_{st}\) for the fuel-rich mixture, the flame thickening in the downstream direction is consistent with the variation of mixture composition in the gaseous phase with increasing \(x/D_{j}\). This behaviour arises due to the smaller droplets being evaporated closer to the jet exit but larger droplets evaporating downstream leading to more fuel-rich conditions in these locations (see Figs. 1b and 3a). Figure 3b shows that as \(x/D_{j}\) increases, the peak mean value of \(\left| {\nabla c} \right|\) shifts towards the burned gas side of the flame. Equations (6)–(9) indicate that the statistical behaviour of \(\left| {\nabla c} \right|\) and its evolution are affected by the flame normal and tangential strain rates induced by fluid motion (i.e. \(a_{N}\) and \(a_{T}\)) and flame propagation (i.e. \(N_{j} \partial S_{d} /\partial x_{j}\) and \(2S_{d} \kappa_{m}\)). Note that the additional strain rates induced by flame propagation (i.e. \(N_{j} \partial S_{d} /\partial x_{j}\) and \(2S_{d} \kappa_{m}\)) are dependent upon the variations of \(S_{d}\) and its components (i.e. \(S_{r}\), \(S_{n}\), \(S_{t}\), \(S_{ev}\) and \(S_{c}\)) which will be discussed next in this paper.

3.2 Displacement Speed Sd Behaviour

The profiles of the mean values of \(S_{d} /S_{L,st}\) and its components (i.e. \(S_{d} /S_{L,st}\), \(S_{r} /S_{L,st}\), \(S_{n} /S_{L,st}\), \(S_{t} /S_{L,st}\), \(S_{ev} /S_{L,st}\), \(S_{c} /S_{L,st}\)) conditional upon \(c\) are shown for \(x/D_{j} = 2\), \(6\) and \(10\) in Fig. 4a–c, respectively where \(S_{L,st}\) is the laminar burning velocity of the stoichiometric mixture. Figure 4a–c exhibit that the mean \(S_{d}\) remains positive with its magnitude increasing with \(c\) for the major part of the flame before reducing and potentially exhibiting negative values towards the burned gas side (see Fig. 4a, b). Figure 4 shows that the mean behaviour of \(S_{d}\) does not change significantly with axial distance from the nozzle, and the mean value of \(S_{r}\) acts as a leading-order contributor, exhibiting positive values increasing in magnitude towards the burned gas side. Figure 4a–c show that the mean contribution of \(S_{n}\) also plays a leading-order role for all axial locations, exhibiting positive values towards the unburned gas side of the flame before exhibiting large negative values towards the burned gas side with a transition close to \(c \approx 0.55\). However, the mean value of \(S_{t}\) has been found to be small in comparison to the mean contributions of \(S_{r}\) and \(S_{n}\) at all axial locations, though its magnitudes have been found to increase with increasing \(x/D_{j}\). Moreover, the mean values of \(S_{ev}\) and \(S_{c}\) remain small in comparison to the mean contributions of \(S_{r}\) and \(S_{n}\) at all axial locations. Accordingly, Fig. 4a–c indicate the behaviour of \(S_{d}\) is principally determined by the competition between \(S_{r}\) and \(S_{n}\) irrespective of the location, which is consistent with the behaviour of \(S_{d}\) and its components in canonical configurations (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a).

Fig. 4
figure 4

Profiles of the mean values of \(S_{d} /S_{L,st}\) [ ] and its components (i.e. \(S_{r} /S_{L,st}\) [ ], \(S_{n} /S_{L,st}\) [ ], \(S_{t} /S_{L,st}\) [ ], \(S_{ev} /S_{L,st}\) [ ] and \(S_{c} /S_{L,st}\) [ ]) conditional upon \(c\) at \(x/D_{j} =\) a \(2\), b \(6\), and c \(10\)

Full size image

3.3 Behaviour of the Fluid Dynamic Strain Rates

The effects of fluid-dynamic straining on the SDF evolution can be understood by analysing the statistical behaviours of \(\nabla \cdot \vec{u}, a_{N}\) and \(a_{T} = \nabla \cdot \vec{u} - a_{N}\), and the profiles of the normalised mean values of these quantities conditional upon \(c\) are presented in Fig. 5a–c, respectively. Figure 5a shows that the mean value of \(\nabla \cdot \vec{u}\) remains positive with decreasing magnitudes exhibited with increasing \(x/D_{j}\). The evaporation of the larger droplets further downstream leads to richer mixtures for the larger \(x/D_{j}\), which reduces the strength of the thermal expansion and this is reflected in the reduced magnitude of the mean values of \(\nabla \cdot \vec{u}\). Figure 5b shows that \(a_{N}\) exhibits predominantly mean positive values but exhibits negative mean values towards the burned gas side of the flame for \(x/D_{j} = 2\). For \(x/D_{j} = 6\) and \(10\), \(a_{N}\) shows negative mean values towards the unburned gas before exhibiting positive mean values towards the middle of the flame, followed by negative values again towards the burned gas. The normal strain rate can be expressed as:

$$a_{N} = \left( {e_{\alpha } \cos^{2} \theta_{\alpha } + e_{\beta } \cos^{2} \theta_{\beta } + e_{\gamma } \cos^{2} \theta_{\gamma } } \right)$$
(11)

where \(e_{\alpha }\), \(e_{\beta }\) and \(e_{\gamma }\) are the most extensive (or positive), intermediate and the most compressive (or negative) principal strain rates, and \(\theta_{\alpha }\), \(\theta_{\beta }\) and \(\theta_{\gamma }\) are the angles between \(\nabla c\) and the eigenvectors associated with \(e_{\alpha }\), \(e_{\beta }\) and \(e_{\gamma }\), respectively. It has been discussed elsewhere (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a; Chakraborty and Swaminathan 2007; Ahmed et al. 2014; Kim and Pitsch 2007) that \(\nabla c\) exhibits collinear alignment between the eigenvector associated with \(e_{\gamma }\) (i.e. \(|\cos \theta_{\gamma } | \approx 1.0\)) when turbulent straining plays a dominant role, whereas a preferential alignment between \(\nabla c\) and the eigenvector associated with \(e_{\alpha }\) (i.e. \(|\cos \theta_{\alpha } | \approx 1.0\)) is observed when the strain rate induced by flame normal acceleration arising from thermal expansion overcomes turbulent straining. A preferential alignment between \(\nabla c\) and the eigenvector associated with \(e_{\alpha }\) (\(e_{\gamma }\)) yields positive (negative) values of \(a_{N}\). The preferential alignment of \(\nabla c\) and the eigenvector associated with \(e_{\gamma }\) in the regions where the effects of thermal expansion are weak leads to negative mean values of \(a_{N}\) towards the burned gas side for all axial locations shown here and also on the unburned gas side for \(x/D_{j} = 6\) and 10. The strain rate induced by thermal expansion overcomes turbulent straining giving rise to a preferential alignment of \(\nabla c\) and the eigenvector associated with \(e_{\alpha }\), which leads to positive mean values of \(a_{N}\) within the flame where heat release effects are strong. The extent of \(\nabla c\) alignment with the eigenvector associated with \(e_{\gamma }\) increases in the downstream direction, and thus the effects of thermal expansion weaken in the axial direction (see Fig. 5a). Accordingly, the mean value of \(a_{N}\) decreases in the in the axial direction and becomes more negative for larger axial distances. The relative magnitudes of the mean values of \(\nabla \cdot \vec{u}\) and \(a_{N}\) determine the mean behaviour of \(a_{T} = \nabla \cdot \vec{u} - a_{N}\). Figure 5c shows that the mean variation of \(a_{T}\) exhibits similar qualitative behaviour at all axial locations (i.e. positive across the flame) but with a decreasing magnitude with increasing \(x/D_{j}\). It is worth noting that the mean value of \(a_{T}\) can be scaled as \(a_{T} \sim{u}^{\prime}/\ell\) (Meneveau and Poinsot 1991) where \(u^{\prime}\) is the rms turbulent velocity fluctuation and \(\ell\) is the integral length scale. Turquand d’Auzay et al. (2019) have demonstrated that for the current cases, \(u^{\prime}\) (\(\ell\)) decreases (increases) with increasing axial distance resulting in reduced magnitudes of \(a_{T}\) with increasing \(x/D_{j}\).

Fig. 5
figure 5

Profiles of the mean values of a \(\nabla \cdot \vec{u} \times \delta_{th,st} /S_{L,st}\), b \(a_{N} \times \delta_{th,st} /S_{L,st}\), and c \(a_{T} \times \delta_{th,st} /S_{L,st}\) conditional upon \(c\) at \(x/D_{j} = 2\) [ ], \(6\) [ ], and \(10\) [ ]

Full size image

3.4 Behaviour of the Strain Rates Induced by Flame Propagation

The profiles of the mean values of \(N_{j} \partial S_{d} /\partial x_{j} \times \delta_{th,st} /S_{L,st}\) and its components (i.e. \(N_{j} \partial (S_{r} + S_{n} )/\partial x_{j} \times \delta_{th,st} /S_{L,st}\), \(N_{j} \partial S_{t} /\partial x_{j} \times \delta_{th,st} /S_{L,st}\), \(N_{j} \partial (S_{ev} + S_{c} )/\partial x_{j} \times \delta_{th,st} /S_{L,st}\)) conditional upon \(c\) are shown in Fig. 6a–d, respectively. Figure 6a shows the mean value of \(N_{j} \partial S_{d} /\partial x_{j}\) remains mostly positive but the magnitude decreases in the downstream direction, which is consistent with previous findings for round jet in premixed flames (Wang et al. 2017). The mean behaviour of \(S_{d}\) is principally determined by the competition between \(S_{r}\) and \(S_{n}\) which is reflected in the mean behaviours of \(N_{j} \partial \left( {S_{r} + S_{n} } \right)/\partial x_{j}\) and \(N_{j} \partial S_{d} /\partial x_{j}\) (see Fig. 6b). The mean contribution of \(N_{j} \partial S_{t} /\partial x_{j}\) is shown to be smaller than that of \(N_{j} \partial \left( {S_{r} + S_{n} } \right)/\partial x_{j}\), and the mean contribution of \(N_{j} \partial \left( {S_{ev} + S_{c} } \right)/\partial x_{j}\) is shown to be negligible. As the mean value of \(N_{j} \partial S_{d} /\partial x_{j}\) remains mostly positive across the flame, it acts to increase the distance between two neighbouring \(c\) iso-surfaces (see Eq. 8).

Fig. 6
figure 6

Profiles of the mean values of a \(N_{j} \partial S_{d} /\partial x_{j} \times \delta_{th,st} /S_{L,st}\), b \(N_{j} \partial \left( {S_{r} + S_{n} } \right)/\partial x_{j} \times \delta_{th,st} /S_{L,st}\), c \(N_{j} \partial S_{t} /\partial x_{j} \times \delta_{th,st} /S_{L,st}\), d \(N_{j} \partial \left( {S_{ev} + S_{c} } \right)/\partial x_{j} \times \delta_{th,st} /S_{L,st}\), and e \(2S_{d} \kappa_{m} \times \delta_{th,st} /S_{L,st}\), f \(2\left( {S_{r} + S_{n} } \right)\kappa_{m} \times \delta_{th,st} /S_{L,st}\), g \(2S_{t} \kappa_{m} \times \delta_{th,st} /S_{L,st}\) and \(2\left( {S_{ev} + S_{c} } \right)\kappa_{m} \times \delta_{th,st} /S_{L,st}\) conditional upon \(c\) at \(x/D_{j} = 2\) [ ], \(6\) [ ], and \(10\) [ ]

Full size image

The profiles of the mean values of \(2S_{d} \kappa_{m} \times \delta_{th,st} /S_{L,st}\) and its components (i.e. \(2(S_{r} + S_{n} )\kappa_{m} \times \delta_{th,st} /S_{L,st}\), \(2S_{t} \kappa_{m} \times \delta_{th,st} /S_{L,st}\), \(2(S_{ev} + S_{c} )\kappa_{m} \times \delta_{th,st} /S_{L,st}\)) conditional upon \(c\) are shown in Fig. 6e–h, respectively. Figure 6e shows \(2S_{d} \kappa_{m}\) exhibits negative mean values across the flame for all axial locations, principally due to the contribution of \(2S_{t} \kappa_{m} = - 4D\kappa_{m}^{2}\) which dominates over the contributions of \(2(S_{r} + S_{n} )\kappa_{m}\) and \(2(S_{ev} + S_{c} )\kappa_{m}\). According to Eq. (9), the negative values observed for \(2S_{d} \kappa_{m}\) across the flame act to decrease flame surface area (i.e. provides a smoothening effect to the wrinkled flame). The mean value of \(2S_{d} \kappa_{m} \times \delta_{th,st} /S_{L,st}\) exhibits similar magnitude across the flame for all axial locations.

3.5 Behaviours of the Effective Strain Rates

The profiles of the mean values of \(N_{j} \partial S_{d} /\partial x_{j} \times \delta_{th,st} /S_{L,st}\), \(a_{N}^{eff} \times \delta_{th,st} /S_{L,st}\) and \(a_{N} \times \delta_{th,st} /S_{L,st}\) conditional upon \(c\) at \(x/D_{j} = 2\), \(6\) and \(10\) are shown in Fig. 7a–c, respectively. The mean behaviour of \(a_{N}^{eff}\) is determined by the combined contributions of \(N_{j} \partial S_{d} /\partial x_{j}\) and \(a_{N}\), and remains positive at all axial locations considered but the magnitude generally decreases with increasing \(x/D_{j}\). According to Eq. (8), this indicates that a positive mean value of \(a_{N}^{eff}\) promotes \(c\) iso-surfaces to be drawn apart leading to flame thickening, which is consistent with the observations made from Fig. 2.

Fig. 7
figure 7

Profiles of the mean values of \(N_{j} \partial S_{d} /\partial x_{j} \times \delta_{th,st} /S_{L,st}\) [ ], \(a_{N}^{eff} \times \delta_{th,st} /S_{L,st}\) [ ], and \(a_{N} \times \delta_{th,st} /S_{L,st}\) [ ] conditional upon \(c\) at \(x/D_{j} =\) a \(2\), b \(6\), and c \(10\)

Full size image

The profiles of the mean values of \(2S_{d} \kappa_{m} \times \delta_{th,st} /S_{L,st}\), \(a_{T}^{eff} \times \delta_{th,st} /S_{L,st}\) and \(a_{T} \times \delta_{th,st} /S_{L,st}\) conditional upon \(c\) at \(x/D_{j} = 2\), \(6\) and \(10\) are shown in Fig. 8a–c, respectively, which show that the mean behaviour of \(a_{T}^{eff}\) changes in the downstream direction. At \(x/D_{j} = 2\) (see Fig. 8a), the negative mean contributions of \(2S_{d} \kappa_{m}\) are overcome by the positive mean contributions of \(a_{T}\) leading to predominantly positive mean values of \(a_{T}^{eff}\) except for the burned gas side where the mean negative contributions of \(2S_{d} \kappa_{m}\) overcome the positive mean values of \(a_{T}\) yielding negative mean values of \(a_{T}^{eff}\). At \(x/D_{j} = 6\) (see Fig. 8b) but with negative mean contributions of \(2S_{d} \kappa_{m}\) start to dominate the positive mean contributions of \(a_{T}\) for most of the flame. Further downstream, though, the negative mean contributions of \(2S_{d} \kappa_{m}\) overcome the positive mean values of \(a_{T}\) resulting in negative mean values of \(a_{T}^{eff}\) across the flame. Equation (9) indicates that a positive (negative) value of \(a_{T}^{eff}\) promotes an increase (decrease) of the flame surface area. Therefore, close to the jet exit, an increase in flame surface area is promoted but, further downstream, the flame surface area decreases and a smoothening of the wrinkled flame front due to flame propagation is expected.

Fig. 8
figure 8

Profiles of the mean values of \(2S_{d} \kappa_{m} \times \delta_{th,st} /S_{L,st}\) [ ], \(a_{T}^{eff} \times \delta_{th,st} /S_{L,st}\) [ ], and \(a_{T} \times \delta_{th,st} /S_{L,st}\) [ ] conditional upon \(c\) at \(x/D_{j} =\) a \(2\), b \(6\), and c \(10\)

Full size image

3.6 Modelling Implications

The statistical behaviours identified in the previous sub-sections are of significant importance from the perspective of modelling turbulent spray flames. It should be noted that the transport equation for the SDF \(\left| {\nabla c} \right|\) can be rewritten in the following form by expanding Eq. (7i):

$$\frac{{\partial \left| {\nabla c} \right|}}{\partial t} + \frac{{\partial \left( {u_{j} \left| {\nabla c} \right| } \right)}}{{\partial x_{j} }} = a_{T} \left| {\nabla c} \right| + 2S_{d} \kappa_{m} \left| {\nabla c} \right| - \frac{{\partial \left( {S_{d} N_{j} \left| {\nabla c} \right| } \right)}}{{\partial x_{j} }}$$
(12i)
$$\frac{{\partial \left| {\nabla c} \right|}}{\partial t} + \frac{{\partial \left( {u_{j} \left| {\nabla c} \right| } \right)}}{{\partial x_{j} }} = a_{T}^{eff} \left| {\nabla c} \right| - \frac{{\partial \left( {S_{d} N_{j} \left| {\nabla c} \right| } \right)}}{{\partial x_{j} }}$$
(12ii)

Furthermore, the transport equation of the generalised FSD (i.e. \({{\Sigma }}_{gen} = \overline{{\left| {\nabla c} \right|}}\)) (Boger et al. 1998; Klein et al. 2018) can be obtained by Reynolds averaging/LES filtering Eqs. (12i) and (12ii). By multiplying Eq. (12i) by 2 \(\left| {\nabla c} \right|\) one obtains:

$$\frac{{\partial \left| {\nabla c} \right|^{2} }}{\partial t} + u_{j} \frac{{\partial \left| {\nabla c} \right|^{2} }}{{\partial x_{j} }} = - 2a_{N} \left| {\nabla c} \right|^{2} - 2N_{j} \frac{{\partial S_{d} }}{{\partial x_{j} }}\left| {\nabla c} \right|^{2} - S_{d} N_{j} \frac{{\partial \left| {\nabla c} \right|^{2} }}{{\partial x_{j} }}$$
(13)

Additionally, algebraic manipulation of Eq. (13) leads to the transport equation of the SDR (\(N_{c} = D\left| {\nabla {\text{c}}} \right|^{2}\)) which can be written as follows (Klein et al. 2018):

$$\begin{aligned} \rho \frac{{\partial N_{c} }}{\partial t} + \rho u_{j} \frac{{\partial N_{c} }}{{\partial x_{j} }} & = - 2\rho a_{N} N_{c} - 2\rho N_{j} \frac{{\partial S_{d} }}{{\partial x_{j} }}N_{c} - \rho S_{d} N_{j} \frac{{\partial N_{c} }}{{\partial x_{j} }} \\ & \quad + \rho S_{d} N_{j} N_{c} \frac{1}{D}\frac{\partial D}{{\partial x_{j} }} + \frac{{\rho N_{c} }}{D}\left( {\frac{\partial D}{\partial t} + u_{j} \frac{\partial D}{{\partial x_{j} }}} \right) \\ \end{aligned}$$
(14i)
$$\begin{aligned} \rho \frac{{\partial N_{c} }}{\partial t} + \rho u_{j} \frac{{\partial N_{c} }}{{\partial x_{j} }} & = - 2\rho a_{N}^{eff} N_{c} - \rho S_{d} N_{j} \frac{{\partial N_{c} }}{{\partial x_{j} }} \\ & \quad + \rho S_{d} N_{j} N_{c} \frac{1}{D}\frac{\partial D}{{\partial x_{j} }} + \frac{{\rho N_{c} }}{D}\left( {\frac{\partial D}{\partial t} + u_{j} \frac{\partial D}{{\partial x_{j} }}} \right) \\ \end{aligned}$$
(14ii)

Upon inspection of Eqs. (12)–(14), it is evident that the statistics of the strain rates \(a_{N}\), \(a_{T}\), \(N_{j} \partial S_{d} /\partial x_{j}\), \(2S_{d} \kappa_{m}\), \(a_{N}^{eff}\) and \(a_{T}^{eff}\) are likely to play a significant role in the transport behaviour of \(\left| {\nabla c} \right|\). As such, the statistical behaviours of these strain rates across turbulent spray flames need to be considered for the satisfactory modelling of the FSD and SDR in the case of turbulent spray combustion. It should be noted that similar behaviours of these strain rates have been observed in the current analysis as those found in turbulent spray flames in canonical configurations (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a), which suggests that the geometrical configuration might not play a major role in the statistical behaviour of SDF and its evolution. Moreover, the SDF statistics show qualitative similarities to the statistics obtained for a bluff body stabilised premixed flame representing experimental burner configurations (Wang et al. 2017; Sandeep et al. 2018). As such, given the found similarities, it is anticipated that the modelling methodologies proposed for turbulent premixed/stratified flames could be extended for turbulent spray flames. It should further be noted that a priori analyses for the development of models for the FSD or SDR approaches in the context of turbulent spray flames will utilise the statistics of the SDF and the strain rates which determine its evolution but the development of new closures for spray combustion requires further consideration of the modelling of unclosed correlations. Whilst such analyses are beyond the scope of the current study, the insights observed from this present analysis are important not only to determine the fundamental insights potential for the differences to those observed in turbulent spray flames of canonical configurations but also as a prelude to developing novel models for turbulent spray flames. Previous studies have investigated a priori modelling of the generalised Flame Surface Density \({{\Sigma }}_{gen} = \overline{{\left| {\nabla c} \right|}}\) in the context of Reynolds Averaged Navier–Stokes and Large Eddy Simulations for turbulent premixed gaseous flames (Chakraborty and Cant 2007; Chakraborty and Cant 2009). The generalised FSD transport equation, which can be obtained by Reynolds averaging/LES filtering the SDF transport equation can be written in the following manner (Candel and Poinsot 1990; Cant et al. 1990; Hawkes 2000; Hawkes and Cant 2001; Chakraborty and Cant 2007, 2009):

$$\frac{{\partial {{\Sigma }}_{gen} }}{\partial t} + \frac{{\partial \left( {\tilde{u}_{j} {{\Sigma }}_{gen} } \right)}}{{\partial x_{j} }} = - \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\overline{{(u_{j} )}}_{s} - \tilde{u}_{j} } \right){{\Sigma }}_{gen} } \right] + \overline{{(a_{T} )}}_{s} {{\Sigma }}_{gen} - \frac{\partial }{{\partial x_{j} }}\left[ {\overline{{(S_{d} N_{j} )}}_{s} {{\Sigma }}_{gen} } \right] + \overline{{\left( {S_{d} \frac{{\partial N_{j} }}{{\partial x_{j} }}} \right)}}_{s} {{\Sigma }}_{gen}$$
(15)

where \(\overline{( \ldots )}_{s} = \overline{{( \ldots )\left| {\nabla c} \right|}} /\overline{{\left| {\nabla c} \right|}}\) represents a suitable surface averaging, overline suggests Reynolds averaging/LES filtering and \((\widetilde{\ldots}) = \overline{( \ldots )\rho } /\bar{\rho }\) represents Favre averaging. In Eq. (15), the first term on the left-hand-side is the transient term and the second is the resolved convection term. The first term on right-hand-side of Eq. (15) is the turbulent transport term, the second term is the strain rate term, the third is the propagation term and the fourth is the curvature term. All of the terms on the right-hand-side of Eq. (15) are unclosed and require modelling. It should be noted that the FSD modelling is not a standard practice for droplet-laden combustion and one needs to understand the SDF statistics first before venturing into the FSD modelling. Moreover, FSD modelling is one of the possibilities that originates from the SDF statistics and one can also obtain SDR modelling related information from the SDF statistics. That said, one can further consider the available statistics to gain some insight into the future modelling of the FSD transport equation. For example, the combined contribution of the curvature and propagation terms in the FSD transport equation can be decomposed into three terms in the following manner (Chakraborty and Cant 2007, 2009; Hawkes 2000; Hawkes and Cant 2001):

$$\overline{{\left( {S_{d} \frac{{\partial N_{j} }}{{\partial x_{j} }}} \right)}}_{s} {{\Sigma }}_{gen} - \frac{\partial }{{\partial x_{j} }}\left[ {\overline{{\left( {S_{d} N_{j} } \right)}}_{s} {{\Sigma }}_{gen} } \right] = {\text{P}}_{mean} + {\text{C}}_{mean} + {\text{C}}_{sg}$$
(16)

where \({\text{P}}_{mean}\) and \({\text{C}}_{mean}\) are the resolved contributions of the propagation and curvature terms, respectively, and \({\text{C}}_{sg}\) is the subgrid component. Expressions for \({\text{P}}_{mean}\) and \({\text{C}}_{mean}\) previously considered for turbulent premixed flames include (Chakraborty and Cant 2007, 2009; Hawkes 2000; Hawkes and Cant 2001):

$${\text{P}}_{mean} = - \frac{\partial }{{\partial x_{j} }}\left[ {\overline{{\left( {S_{d} } \right)}}_{s} \overline{{(N_{j} )}}_{s} {{\Sigma }}_{gen} } \right]$$
(17i)
$${\text{C}}_{mean} = \overline{{(S_{d} )}}_{s} \frac{{\partial \overline{{(N_{j} )}}_{s} }}{{\partial x_{j} }}{{\Sigma }}_{gen}$$
(17ii)

It has previously been noted that non-linear dependence of curvature on the curvature and propagation terms observed in turbulent premixed flames (Chakraborty and Cant 2007) can only be accounted for if the curvature effect on \(S_{d}\) is taken into account in the modelling. Table 1 exemplarily presents the \(S_{d} - \kappa_{m}\) correlations at \(c = 0.7\) for the different axial locations considered. It is evident from Table 1 that \(S_{d} - \kappa_{m}\) are negatively correlated and qualitatively similar behaviour has been observed for other values of \(c\). This is consistent with previous analyses of turbulent premixed flames (Chakraborty and Cant 2007) and suggests that the correlation between \(S_{d}\) and \(\kappa_{m} = 0.5\left( {\partial N_{j} /\partial x_{j} } \right)\) cannot be neglected while modelling the FSD curvature term \(\overline{{\left( {2S_{d} \kappa_{m} } \right)}}_{s} {{\Sigma }}_{gen}\), which is the area-weighted value of curvature stretch rate (or alternatively the area-weighted value of tangential strain rate induced by flame propagation). Moreover, the FSD curvature term \(\overline{{\left( {2S_{d} \kappa_{m} } \right)}}_{s} {{\Sigma }}_{gen}\) cannot be adequately approximated by \({\text{C}}_{mean}\) which disregards the interrelation between \(S_{d}\) and \(\kappa_{m}\). Therefore, the modelling of \({\text{C}}_{sg}\) will be of critical importance for the purpose of modelling the FSD curvature term. Given the qualitative similarities between the curvature dependences of the flame displacement speed for premixed and spray flames, it can be expected that the modelling methodologies for \({\text{C}}_{sg}\) for turbulent premixed combustion have the potential to be applied for turbulent spray flames.

Table 1 Correlations of \(S_{d} - \kappa_{m}\), \(S_{d} - N_{1}\), \(S_{d} - N_{2}\) and \(S_{d} - N_{3}\) on \(c = 0.7\) isosurface at \(x/D_{j} = 2\), \(6\) and \(10\)
Full size table

The expression for \({\text{P}}_{mean}\) (i.e. Eq. 17i) implicitly assumes that the displacement speed \(S_{d}\) and the flame normal vector components (i.e. \(N_{1}\), \(N_{2}\), \(N_{3}\)) are uncorrelated. The correlations of displacement speed \({\text{S}}_{d}\) and the flame normal vector components (i.e. \(N_{1}\), \(N_{2}\), \(N_{3}\)) are exemplarily presented in Table 1 at \(c = 0.7\) for each of the axial locations considered but similar qualitative behaviour has been observed for other values of \(c\). It is evident from Table 1 that displacement speed \({\text{S}}_{d}\) and the flame normal vector components (i.e. \(N_{1}\), \(N_{2}\), \(N_{3}\)) are weakly correlated at each of the axial locations considered. This implies that \({\text{P}}_{mean}\) can be used to close the FSD propagation term \(- \partial \left[ {\overline{{\left( {S_{d} N_{j} } \right)}}_{s} {{\Sigma }}_{gen} } \right]/\partial x_{j}\) without any additional modelling provided that \((\overline{{S_{d} }} )_{s}\) and \(\overline{{(N_{j} )}}_{s}\) are suitably modelled.

It should be noted that the \(j{\text{th}}\) component of the flame normal vector, \(\overline{{(N_{j} )}}_{s}\), is given as (Chakraborty and Cant 2007, 2009; Hawles 2000; Hawkes and Cant 2001):

$$\overline{{(N_{j} )}}_{s} = - \frac{1}{{{{\Sigma }}_{gen} }}\frac{{\partial \bar{c}}}{{\partial x_{j} }}$$
(18)

In the context of the generalised FSD, Eq. (18) is an exact expression and has previously been proposed in the context of RANS and LES simulations (Chakraborty and Cant 2007, 2009;  Hawkes 2000; Hawkes and Cant 2001; Cant et al. 1990). From the perspective of modelling of \(\overline{{\left( {S_{d} } \right)}}_{s}\), in the context of FSD modelling, the following relationship is often invoked (Hawkes 2000; Hawkes and Cant 2001):

$$\overline{{\left( {\rho S_{d} } \right)}}_{s} {{\Sigma }}_{gen} = \overline{{\left( {\rho S_{d} \left| {\nabla c} \right|} \right)}} \approx \rho_{0} S_{b\left( \phi \right)} {{\Sigma }}_{gen} = \rho_{0} S_{b\left( \phi \right)} \overline{{\left| {\nabla c} \right|}}$$
(19)

where \(\rho_{0}\) is the unburned reactant density and \(S_{b\left( \phi \right)}\) is the laminar burning speed as a function of the local equivalence ratio . The variations of the mean values of \((\rho S_{d} |\nabla c|)\) and \((\rho_{0} S_{b\left( \phi \right)} |\nabla c|)\) across \(c\) at each of the axial locations considered are shown in Fig. 9. It is evident from Fig. 9 that the mean value of \((\rho_{0} S_{b\left( \phi \right)} |\nabla c|)\) remains different from \(\overline{{\left( {\rho S_{d} \left| {\nabla c} \right|} \right)}}\) across \(c\) for all of the axial locations considered. Thus, the approximation \(\overline{{\left( {\rho S_{d} } \right)}}_{s} {{\Sigma }}_{gen} \approx \rho_{0} S_{b\left( \phi \right)} {{\Sigma }}_{gen}\) (Hawkes 2000; Hawkes and Cant 2001) may not be valid for turbulent spray flames. Finally, the statistics of \(a_{T}\) in Fig. 5 and the associated discussion suggest that the modelling of the tangential strain rate term \(\overline{{(a_{T} )}}_{s} {{\Sigma }}_{gen}\) in Eq. (15) depends on the accurate incorporation of dilatation rate \(\nabla \cdot \vec{u}\) and the alignment of \(\nabla c\) with local principal directions, as discussed in the context of Fig. 5. Such a priori modelling of the FSD is indeed beyond the scope of the current study. However, these aspects will form the basis of future investigations.

Fig. 9
figure 9

Variations of the mean values of \(\left( {\rho S_{d} \left| {\nabla c} \right|} \right) \times \delta_{th,st} /S_{L,st}\) [ ] and \(\left( {\rho_{0} S_{b\left( \phi \right)} \left| {\nabla c} \right|} \right) \times \delta_{th,st} /S_{L,st}\) [ ] conditional upon \(c\) at a \(x/D_{j} = 2\), b \(x/D_{j} = 6\) and c \(x/D_{j} = 10\)

Full size image

The above discussion with regards to the insights into the statistical aspects of the study of the SDF evolution and the a priori modelling of the FSD indicates that further analysis is still required. The unclosed terms of the FSD transport equation (i.e. turbulent transport term, strain rate term, propagation term and curvature term) all require modelling. Such a priori modelling has not been considered based on an open turbulent jet spray flame in the presence of a shear layer and will contribute important novel insights. However, such analyses are not trivial and are, therefore, beyond the scope of the current study but will form the basis of future investigations.

4 Conclusions

A three-dimensional Direct Numerical Simulation database of an open turbulent jet spray flame representing a laboratory-scale burner configuration (Gounder et al. 2012) has been analysed to investigate the statistical behaviours of the SDF \(\left| {\nabla {\text{c}}} \right|\) and the quantities affecting its evolution (i.e. \({\text{S}}_{d}\), \(\nabla \cdot \vec{u}\), \(a_{N}\), \(a_{T}\), \(N_{j} \partial S_{d} /\partial x_{j}\), \(2S_{d} \kappa_{m}\), \(a_{N}^{eff} = a_{N} + N_{j} \partial S_{d} /\partial x_{j}\) and \(a_{T}^{eff} = a_{T} + 2S_{d} \kappa_{m}\)). The flame in question has been found to exhibit predominantly fuel-rich conditions and this tendency strengthens further in the downstream direction due to the evaporation of fuel droplets. This behaviour significantly affects the statistical behaviours of \({\text{S}}_{d}\), \(\nabla \cdot \vec{u}\), \(a_{N}\), \(a_{T}\), \(N_{j} \partial S_{d} /\partial x_{j}\), \(2S_{d} \kappa_{m}\), \(a_{N}^{eff}\) and \(a_{T}^{eff}\). The mean SDF decreases downstream of the jet exit indicating progressive flame thickening in the downstream direction. For all axial locations considered, the behaviour of \({\text{S}}_{d}\) is principally determined by the competition between \(S_{r}\) and \(S_{n}\) with the mean contributions \(S_{t}\), \(S_{ev}\) and \(S_{c}\) all being small in comparison to leading order mean contribution of \((S_{r} + S_{n} )\), which in turn affect the mean behaviours of \(N_{j} \partial S_{d} /\partial x_{j}\) and \(2S_{d} \kappa_{m}\). The relative magnitudes of \(\nabla \cdot \vec{u}\) and \(a_{N}\) result in positive mean values of \(a_{T}\) with reducing magnitudes moving downstream of the jet exit. The normal strain rate induced by flame propagation \(N_{j} \partial S_{d} /\partial x_{j}\) has been found to exhibit positive mean values across the flame for all axial locations but the magnitude reduces in the downstream direction. The curvature stretch rate \(2S_{d} \kappa_{m}\) has been found to exhibit negative mean values across the flame for all axial locations. The mean effective normal strain rate \(a_{N}^{eff}\) has been found to be positive across the flame but reduces in magnitude moving away from the jet exit. These positive mean values of \(a_{N}^{eff}\) indicate flame thickening behaviour in a mean sense. The effective tangential strain rate (or stretch rate) \(a_{T}^{eff}\) has been found to exhibit mean positive values across the flame close to the jet exit (indicating an increase in the flame surface area) but negative mean values across the flame in the downstream (indicating a decrease in the flame surface area). Similar behaviours of the strain rates affecting the SDF evolution have been observed in the current analysis as those found in turbulent spray flames in canonical configurations (Wacks and Chakraborty 2016; Ozel Erol et al. 2019a), which suggests that the geometrical configuration might not play a major role in the statistical behaviour of SDF and its evolution in the case of turbulent spray flames. However, further examination of different flame configurations will be required to test the veracity of this hypothesis. Furthermore, the SDF statistics discussed in this paper show qualitative similarities to the corresponding statistics obtained for a premixed jet flame and a bluff body stabilised premixed flame where both flames represent experimental burner configurations (Wang et al. 2017; Sandeep et al. 2018). Given these similarities, it is expected that the modelling methodologies proposed for turbulent premixed/stratified flames might be extended for turbulent spray flames, which will form the basis of future investigations.