Skip to main content
SpringerLink
Log in

Travel time prediction with viscoelastic traffic model

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

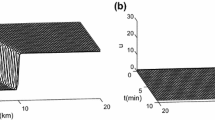
Travel time through a ring road with a total length of 80 km has been predicted by a viscoelastic traffic model (VEM), which is developed in analogous to the non-Newtonian fluid flow. The VEM expresses a traffic pressure for the unfree flow case by space headway, ensuring that the pressure can be determined by the assumption that the relevant second critical sound speed is exactly equal to the disturbance propagation speed determined by the free flow speed and the braking distance measured by the average vehicular length. The VEM assumes that the sound speed for the free flow case depends on the traffic density in some specific aspects, which ensures that it is exactly identical to the free flow speed on an empty road. To make a comparison, the open Navier-Stokes type model developed by Zhang (ZHANG, H. M. Driver memory, traffic viscosity and a viscous vehicular traffic flow model. Transp. Res. Part B, 37, 27–41 (2003)) is adopted to predict the travel time through the ring road for providing the counterpart results. When the traffic free flow speed is 80 km/h, the braking distance is supposed to be 45 m, with the jam density uniquely determined by the average length of vehicles l ≈ 5.8 m. To avoid possible singular points in travel time prediction, a distinguishing period for time averaging is pre-assigned to be 7.5 minutes. It is found that the travel time increases monotonically with the initial traffic density on the ring road. Without ramp effects, for the ring road with the initial density less than the second critical density, the travel time can be simply predicted by using the equilibrium speed. However, this simpler approach is unavailable for scenarios over the second critical.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A :

Jacobian matrix

B :

parameter used in Eq. (3)

B 0 :

parameter defined by Eq. (9)

B 1 :

= 2ux

B * :

parameter defined by Eq. (7)

c :

traffic sound speed (m/s)

c 0 :

sound speed at critical density ρc2 (m/s)

c τ :

speed depending on vf and xbr

E 2 :

parameter defined by Eq. (22)

F :

= (q, q2/ρ + p)T, flux vector

Fi+1/2 :

numerical flux at xi+1/2

G :

modulus of fluid elasticity used in Eq. (1)

K :

model parameter used in Eq. (4)

l :

average length of vehicles

l 0 :

length scale (m)

n :

time level

p :

traffic pressure (ρmvf2)

q :

= ρu, traffic flow rate (veh/s), where veh means vehiles

q e :

= ρue, equilibrium traffic flow rate (veh/s)

R :

defined by Eq. (13)

R 1 :

= R + c2ρx

t :

time (s)

t 0 :

time scale (s)

t end :

time of simulation ended (s)

T tav :

mean travel time (s)

T′ t :

root mean square (rms) of travel time (s)

U :

= (ρ, q), solution vector

u :

traffic speed (m/s)

u e :

equilibrium traffic speed (m/s)

u c2 :

second critical speed (m/s)

v 0 :

speed scale (m/s)

v f :

free flow speed (m/s)

x :

coordinate (m)

X br :

braking distance of vehicles (m)

α :

= lρm, parameter used to describe traffic pressure and sound speed

β 0 :

parameter used to define traffic pressure

β :

= v/2τ0c02

Δt :

time step (s)

Δx :

mesh length (m)

Δ0 :

preassigned distinguishing period (s)

λk :

eigenvalues of Eq. (14)

Λ:

= cτ/uc2

ρ :

traffic density (kg/m3)

ρ*:

first critical density (veh/km)

ρ s :

saturation density (veh/km)

ρ m :

traffic jam density (veh/km)

ρ c2 :

second critical density (veh/km)

ρ 0 :

initial density on the ring road (veh/km)

ω :

=Δt/Δx, ratio of time step to spatial mesh length

v :

fluid kinematic viscosity (m2/s)

τ :

relaxation time (s)

τ 0 :

relaxation time relevant to speed c0 (m2/s).

References

  1. LIGHTHILL, M. J. and WHITHAM, G. B. On kinematic waves ii: a theory of traffic flow on long crowded roads. Proc. Roy. Soc. Lond A, 229, 317–345 (1955)

    Article  MathSciNet  MATH  Google Scholar 

  2. RICHARDS, P. I. Shock waves on the freeway. Operations Res., 4, 42–51 (1956)

    Article  MathSciNet  Google Scholar 

  3. PAYNE, H. J. Models of freeway traffic and control. Mathematical Model of Public Systems, Simulation Council Proc. La Jola California, 1, 51–61 (1971)

    Google Scholar 

  4. HELBING, D. and TREIBER, M. Gas-kinetic-based traffic model explaining observed hysteretic phase transition. Phys. Rev. Lett., 81, 3042–3045 (1998)

    Article  Google Scholar 

  5. HOOGENDOORN, S. P. and BOVY, P. H. L. Continuum modeling of multiclass traffic flow. Transp. Res. Part B, 34(2), 123–146 (2000)

    Article  Google Scholar 

  6. KERNER, B. S. and KONH¨AUSER, P. Cluster effect in initially homogemeous traffic flow. Phys. Rev. E, 48, 2335–2338 (1993)

    Article  Google Scholar 

  7. GREENBERG, J. M. Congestion redux. SIAM J. Appl. Math., 64(4), 1175–1185 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  8. BORSCHE, R., KIMATHI, M., and KLAR, A. A class of multi-phase traffic theories for microscopic, kinetic and continuum traffic models. Computers and Mathematics with Applications, 64, 2939–2953 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  9. LEBACQUE, J. P., MAMMAR, S., and HAJ-SALEM, H. Generic Second Order Traffic Flow Modelling. Transportation and Traffic Theory (eds. ALLSOP, R. E. and BENJIAMIN, G. H.) Oxford, 755–776 (2007)

  10. LEBACQUE, J. P. and KHOSHYARAN, M. M. A variational formulation for higher order macroscopic traffic flow models of the gsom family. Transp. Res. Part B, 57, 245–265 (2013)

    Article  Google Scholar 

  11. ZHANG, P., WONG, S. C., and DAI, S. Q. A conserved higher order aniso-tropic traffic flow model: description of equilibrium and non-equilibrium flows. Transp. Res. Part B, 43(5), 562–574 (2009)

    Article  Google Scholar 

  12. FLYNN, M. R., KASIMOV, A. R., NAVE, J. C., ROSALES, R. R., and SEIBOLD, B. Selfsustained nonlinear waves in traffic flow. Phys. Rev. E, 79, 056113 (2009)

    Article  MathSciNet  Google Scholar 

  13. HELBING, D. Traffic and related self-driven many-particle systems. Rev. Mod. Phys., 73, 1067–1141 (2001)

    Article  Google Scholar 

  14. NAGATANI, T. The physics of traffic jams. Rep. Prog. Phys., 65, 1331–1386 (2002)

    Article  Google Scholar 

  15. BRACKSTONE, M. and MCDONALD, M. Car-following: a historical review. Transp. Res. Part F, 2, 181–196 (1999)

    Article  Google Scholar 

  16. NAGEL, K. and SCHRECKENBERG, M. A cellular automaton model for freeway traffic. J. De Phys. I, 2(12), 2221–2229 (1992)

    Google Scholar 

  17. HELBING, D. and HUBERMAN, B. A. Coherent moving states in highway traffic. nature, 396 (6713), 738–740 (1998)

    Article  Google Scholar 

  18. CHOWDHURY, D., SANTEN, L., and SCHADSSCHNEIDER, A. Statistical physics of vehicular traffic and some related systems. Physics Reports, 329, 199–329 (2000)

    Article  MathSciNet  Google Scholar 

  19. NGODUY, D. Application of gas-kinetic theory to modelling mixed traffic of manual and adaptive cruise control vehicles. Transportmetrica A: Transport Science, 8(1), 43–60 (2012)

    Article  Google Scholar 

  20. NGODUY, D. Platoon-based macroscopic model for intelligent traffic flow. Transportmetrica B: Transport Dynamics, 1(2), 153–169 (2013)

    Google Scholar 

  21. LI, J. and ZHANG, H. M. The variational formulation of a non-equilibrium traffic flow model: theory and implications. Procedia-Social and Behavioral Sciences, 80, 327–340 (2013)

    Article  Google Scholar 

  22. ZHU, Z. J. and YANG, C. Visco-elastic traffic flow model. J. Advanced Transp., 47, 635–649 (2013)

    Article  Google Scholar 

  23. TORDEUX, A., ROUSSIGNOL, M., LEBACQUE, J. P., and LASSARRE, S. A stochastic jump process applied to traffic flow modelling. Transportmetrica A: Transport Science, 10(4), 350–375 (2014)

    Article  Google Scholar 

  24. COSTESEQUE, G. and LEBACQUE, J. P. A variational formulation for higher order macroscopic traffic flow models: numerical investigation. Transp. Res. Part B, 70, 112–133 (2014)

    Article  Google Scholar 

  25. BOGDANOVA, A. I., SMIRNOVA, M. N., ZHU, Z. J., and SMIRNOV, N. N. Exploring peculiarities of traffic flows with a viscoelastic model. Transportmetrica A: Transport Science, 11(7), 561–578 (2015)

    Article  Google Scholar 

  26. SMIRNOVA, M. N., BOGDANOVA, A. I., ZHU, Z. J., and SMIRNOV, N. N. Traffic flow sensitivity to viscoelasticity. Theoretical and Applied Mechanics Letters, 6, 182–185 (2016)

    Article  Google Scholar 

  27. SMIRNOVA, M. N., BOGDANOVA, A. I., ZHU, Z. J., and SMIRNOV, N. N. Traffic flow sensitivity to parameters in viscoelastic modelling. Transportmetrica B: Transport Dynamics, 5(1), 115–131 (2017)

    Google Scholar 

  28. ZHANG, Y. L., SMIRNOVA, ¡. N., BOGDANOVA, A. I., ZHU, Z. J., and SMIRNOV, N. N. Travel time estimation by urgent-gentle class traffic flow model. Transp. Res. Part B, 113, 121–142 (2018)

    Article  Google Scholar 

  29. CHANG, G. L. and MAHMASSANI, H. S. Travel time prediction and departure time adjustment behavior dynamics in a congested traffic system. Transp. Res. Part B, 22, 217–232 (1988)

    Article  Google Scholar 

  30. DAILEY, D. J. Travel-time estimation using cross-correlation techniques. Transp. Res. Part B, 27(2), 97–107 (1993)

    Article  Google Scholar 

  31. LINT, J. V. and DER ZIJPP, N. V. Improving a travel-time estimation algorithm by using dual loop detectors. Transp. Res. Rec., 1855, 41–48 (2003)

    Article  Google Scholar 

  32. CHIEN, S. I. J. and KUCHIPUDI, C. M. Dynamic travel time prediction with real-time and historic data. ASCE J. Transp. Eng., 129(6), 608–616 (2003)

    Article  Google Scholar 

  33. WU, C. H., MO, J. M., and LEE, D. T. Travel-time prediction with support vector regression. IEEE Trans. Intell. Transp. Syst., 5(4), 276–281 (2004)

    Article  Google Scholar 

  34. VAN LINT, J. W. C., HOOGENDOORN, S. P., and VAN ZUYLEN, H. J. Accurate freeway travel time prediction with state-space neural networks under missing data. Transp. Res. Part C, 13, 347–369 (2005)

    Article  Google Scholar 

  35. HOFLEITNER, A., HERRING, R., and BAYEN, A. Arterial travel time forecast with streaming data: a hybrid approach of flow modeling and machine learning. Transp. Res. Part B, 46, 1097–1122 (2012)

    Article  Google Scholar 

  36. RAMEZANI, M. and GEROLIMINIS, N. On the estimation of arterial route travel time distribution with markov chains. Transp. Res. Part B, 46, 1576–1590 (2012)

    Article  Google Scholar 

  37. JENELIUS, E. and KOUTSOPOULOS, H. N. Travel time estimation for urban road networks using low frequency probe vehicle data. Transp. Res. Part B, 53, 64–81 (2013)

    Article  Google Scholar 

  38. YILDIRIMOGLU, M. and GEROLIMINIS, N. Experienced travel time prediction for congested freeways. Transp. Res. Part B, 53, 45–63 (2013)

    Article  Google Scholar 

  39. HANS, E., CHIABAUT, N., and LECLERCQ, L. Applying variational theory to travel time estimation on urban arterials. Transp. Res. Part B, 78, 169–181 (2015)

    Article  Google Scholar 

  40. KUMAR, B. A., VANAJAKSHI, L., and SUBRAMANIAN, S. C. Bus travel time prediction using a time-space discretization approach. Transp. Res. Part C, 79, 308–332 (2017)

    Article  Google Scholar 

  41. CHANG, G. L. and MAHMASSANI, H. S. Travel time prediction and departure time adjustment behavior dynamics in a congested traffic system. Transp. Res. Part B, 22, 217–232 (1988)

    Article  Google Scholar 

  42. MA, Z. L., KOUTSOPOULOS, H. N., FERREIRA, L., and MESBAH, M. Estimation of trip travel time distribution using a generalized markov chain approach. Transp. Res. Part C, 74, 1–21 (2017)

    Article  Google Scholar 

  43. RAHMANI, M., KOUTSOPOULOS, H. N., and JENELIUS, E. Travel time estimation from sparse floating car data with consistent path inference: a fixed point approach. Transp. Res. Part C, 85, 628–643 (2017)

    Article  Google Scholar 

  44. ZHANG, H. M. Driver memory, traffic viscosity and a viscous vehicular traffic flow model. Transp. Res. Part B, 37, 27–41 (2003)

    Article  Google Scholar 

  45. DEL CALSTILLO, J. M. Propagation of perturbations in dense traffic flow: a model and its implications. Transp. Res. Part B, 35, 367–389 (2001)

    Article  Google Scholar 

  46. HILLIGES, M. and WEIDLICH, W. A phenomenological model for dynamic traffic flow in networks. Transp. Res. Part B, 29(6), 407–431 (1995)

    Article  Google Scholar 

  47. KERNER, B. S. Synchronized flow as a new traffic phase and related problems for traffic flow modelling. Mathematical and Computer Modelling, 35, 481–508 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  48. SCHÖNHOF, M. and HELBING, D. Criticism of three-phase traffic theory. Transp. Res. Part B, 43, 784–797 (2009)

    Article  Google Scholar 

  49. HAN, S. F. Constitutive Theory of Viscoelastic Fluids (in Chinese), Science Press, Beijing, 59–86 (2000)

    Google Scholar 

  50. SMIRNOV, N. N., KISELEV, A. B., NIKITIN, V. F., SILNIKOV, V. F., and MANENKOVA, A. S. Hydrodynamic traffic flow models and its application to studying traffic control effectiveness. WSEAS Transactions on Fluid Mechanics, 9, 178–186 (2014)

    Google Scholar 

  51. SMIRNOV, N. N., KISELEV, A. B., NIKITIN, V. F., and YUMASHEV, M. V. Mathematical modelling of road traffic flows. Moscow University Mechanics Bulletin, 55(4), 12–18 (2000)

    MATH  Google Scholar 

  52. KISELEV, A. B., KOKOLEVA, A. V., NIKITIN, V. F., and SMIRNOV, N. N. Mathematical modeling of traffic flow on controled roads. J. Appl. Math. Mech., 68, 933–939 (2004)

    Article  Google Scholar 

  53. SMIRNOVA, M. N., BOGDANOVA, A. I., ZHU, Z. J., MANENKOVA, A. S., and SMIRNOV, N. N. Mathematical modeling of traffic flows using continuum approach: visco-elastic effect in traffic flows (in Russian). Mathem. Mod., 26, 54–64 (2014)

    MATH  Google Scholar 

  54. AW, A. and RASCLE, M. Resurrection of second order models of traffic flow. SIAM J. Appl. Math., 60, 916–938 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  55. KLAR, A. and WEGENER, R. Kinetic derivation of macroscopic anticipation models for vehicular traffic. SIAM J. Appl. Math., 60, 1749–1766 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  56. KISELEV, A. B., NIKITIN, V. F., SMIRNOV, N. N., and YUMASHEV, M. V. Irregular traffic flow on a ring road. J. Appl. Math. Mech., 64(4), 627–634 (2000)

    Article  MATH  Google Scholar 

  57. ZHU, Z. J., WU, Q. S., JIANG, R., and WU, T. Q. Numerical study on traffic flow with single parameter state equation. ASCE J. Transp. Engineering, 128, 167–172 (2002)

    Article  Google Scholar 

  58. HAIGHT, F. A. Mathematical Theories of Traffic Flow, Academic Press, New York, 89–92 (1963)

    MATH  Google Scholar 

  59. MA. J., CHAN, C. K., YE, Z. B., and ZHU, Z. J. Effects of maximum relaxation in viscoelastic traffic flow modeling. Transp. Res. Part B, 113, 143–163 (2018)

    Article  Google Scholar 

  60. DAGANZO, C. F. Requiem for second-order fluid approximations of traffic flow. Transp. Res. Part B, 29, 277–286 (1995)

    Article  Google Scholar 

  61. RASCLE, M. An improved macroscopic model of traffic flow: derivation and links with the lighthill-whitham model. Mathematical and Computer Modelling, 35, 581–590 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  62. XU, R. Y., ZHANG, P., DAI, S. C., and WONG, S. C. Admissibility of a wide cluster solution inanisotropic higher-order traffic flow models. SIAM J. Appl. Math., 68(2), 562–573 (2007)

    Article  MATH  Google Scholar 

  63. ROE, P. C. Approximate riemann solver, parameter vectors, and difference schemes. J. Comput. Phys., 43, 357–372 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  64. SHUI, H. S. Finite Difference in One-dimensional Fluid Mechanics (in Chinese), National Defense, Beijing, 333–355 (1998)

    Google Scholar 

  65. ZHU, Z. J. and WU, T. Q. Two-phase fluids model for freeway traffic and its application to simulate the evolution of solitons in traffic. ASCE J. Transp. Engineering, 129, 51–56 (2003)

    Article  Google Scholar 

  66. CHANG, G. L. and ZHU, Z. J. A macroscopic traffic model for highway work zones: formulations and numerical results. J. Advanced Transp., 40(3), 265–287 (2006)

    Article  Google Scholar 

  67. TAO, W. Q. Numerical Heat Transfer (in Chinese), Xian Jiaotong University Press, Xi’an, 195–251 (2001)

    Google Scholar 

  68. DAGANZO, C. F. Fundamentals of Transportation and Traffic Operations, Pergamon, New York, 110–112 (1997)

    Book  Google Scholar 

  69. MCSHANE, W. R., ROESS, R. P., and PRASSAS, E. S. Traffic Engineering, Chap. 12, 2nd ed., Prentice-Hall, New Jersey, 282–306 (1998)

    Google Scholar 

  70. DRAKE, J. S., SCHOFER, J. L., and MAY, A. D., JR. A statistical analysis of speed-density hypothesis. Transportation Research Record, 154, 81–82 (1967)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Engineering Science, University of Science and Technology of China, Hefei, 230026, China

    Yongliang Zhang & Zuojin Zhu

  2. Faculty of Mechanics and Mathematics, Moscow M. V. Lomonosov State University, Moscow, 119992, Russia

    M. N. Smirnova, A. I. Bogdanova, Zuojin Zhu & N. N. Smirnov

  3. Scientific Research Institute for System Analysis, Russian Academy of Sciences, Moscow, 117312, Russia

    N. N. Smirnov

Authors
  1. Yongliang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. N. Smirnova
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. I. Bogdanova
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zuojin Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. N. N. Smirnov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. N. Smirnov.

Additional information

Project supported by the Russian Foundation for Basic Research (No. 18-07-00518) and the National Natural Science Foundation of China (No. 10972212)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., Smirnova, M.N., Bogdanova, A.I. et al. Travel time prediction with viscoelastic traffic model. Appl. Math. Mech.-Engl. Ed. 39, 1769–1788 (2018). https://doi.org/10.1007/s10483-018-2400-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-018-2400-9

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation