Skip to main content
SpringerLink
Log in

The effect of initial geometric imperfection on the nonlinear resonance of functionally graded carbon nanotube-reinforced composite rectangular plates

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

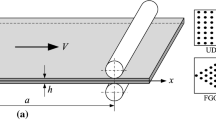
The purpose of the present study is to examine the impact of initial geometric imperfection on the nonlinear dynamical characteristics of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) rectangular plates under a harmonic excitation transverse load. The considered plate is assumed to be made of matrix and single-walled carbon nanotubes (SWCNTs). The rule of mixture is employed to calculate the effective material properties of the plate. Within the framework of the parabolic shear deformation plate theory with taking the influence of transverse shear deformation and rotary inertia into account, Hamilton’s principle is utilized to derive the geometrically nonlinear mathematical formulation including the governing equations and corresponding boundary conditions of initially imperfect FG-CNTRC plates. Afterwards, with the aid of an efficient multistep numerical solution methodology, the frequency-amplitude and forcing-amplitude curves of initially imperfect FG-CNTRC rectangular plates with various edge conditions are provided, demonstrating the influence of initial imperfection, geometrical parameters, and edge conditions. It is displayed that an increase in the initial geometric imperfection intensifies the softening-type behavior of system, while no softening behavior can be found in the frequency-amplitude curve of a perfect plate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. BOUNOUARA, F., BENRAHOU, K. H., BELKORISSAT, I., and TOUNSI, A. A nonlocal zeroth-order shear deformation theory for free vibration of functionally graded nanoscale plates resting on elastic foundation. Steel and Composite Structures, 20(2), 227–249 (2016)

    Article  Google Scholar 

  2. BELLIFA, H., BENRAHOU, K. H., BOUSAHLA, A. A., TOUNSI, A., and MAHMOUD, S. A nonlocal zeroth-order shear deformation theory for nonlinear postbuckling of nanobeams. Structural Engineering and Mechanics, 62(6), 695–702 (2017)

    Google Scholar 

  3. BOUAFIA, K., KACI, A., HOUARI, M. S. A., BENZAIR, A., and TOUNSI, A. A nonlocal quasi-3D theory for bending and free flexural vibration behaviors of functionally graded nanobeams. Smart Structures and Systems, 19(2), 115–126 (2017)

    Article  Google Scholar 

  4. BESSEGHIER, A., HOUARI, M. S. A., TOUNSI, A., and MAHMOUD, S. Free vibration analysis of embedded nanosize FG plates using a new nonlocal trigonometric shear deformation theory. Smart Structures and Systems, 19(6), 601–614 (2017)

    Google Scholar 

  5. THOSTENSON, E. T., REN, Z., and CHOU, T. W. Advances in the science and technology of carbon nanotubes and their composites: a review. Composites Science and Technology, 61(13), 1899–1912 (2001)

    Article  Google Scholar 

  6. LAU, A. K. T. and HUI, D. The revolutionary creation of new advanced materials—carbon nanotube composites. Composites Part B: Engineering, 33(4), 263–277 (2002)

    Article  Google Scholar 

  7. WANG, M., LI, Z. M., and QIAO, P. Semi-analytical solutions to buckling and free vibration analysis of carbon nanotube-reinforced composite thin plates. Composite Structures, 144, 33–43 (2016)

    Article  Google Scholar 

  8. GEORGE, N., JEYARAJ, P., and MURIGENDRAPPA, S. Buckling and free vibration of nonuniformly heated functionally graded carbon nanotube reinforced polymer composite plate. International Journal of Structural Stability and Dynamics, 17, 1750064 (2016)

    Article  Google Scholar 

  9. ANSARI, R., SHOJAEI, M. F., MOHAMMADI, V., GHOLAMI, R., and SADEGHI, F. Nonlinear forced vibration analysis of functionally graded carbon nanotube-reinforced composite Timoshenko beams. Composite Structures, 113, 316–327 (2014)

    Article  Google Scholar 

  10. WU, H., KITIPORNCHAI, S., and YANG, J. Thermal buckling and postbuckling analysis of functionally graded carbon nanotube-reinforced composite beams. Applied Mechanics and Materials, 846, 182–187 (2016)

    Article  Google Scholar 

  11. CIVALEK, Ö. Free vibration of carbon nanotubes reinforced (CNTR) and functionally graded shells and plates based on FSDT via discrete singular convolution method. Composites Part B: Engineering, 111, 45–59 (2017)

    Article  Google Scholar 

  12. MEHRI, M., ASADI, H., and WANG, Q. Buckling and vibration analysis of a pressurized CNT reinforced functionally graded truncated conical shell under an axial compression using HDQ method. Computer Methods in Applied Mechanics and Engineering, 303, 75–100 (2016)

    Article  MathSciNet  Google Scholar 

  13. PHUNG-VAN, P., ABDEL-WAHAB, M., LIEW, K., BORDAS, S., and NGUYEN-XUAN, H. Isogeometric analysis of functionally graded carbon nanotube-reinforced composite plates using higher-order shear deformation theory. Composite Structures, 123, 137–149 (2015)

    Article  Google Scholar 

  14. SONG, Z., ZHANG, L., and LIEW, K. Vibration analysis of CNT-reinforced functionally graded composite cylindrical shells in thermal environments. International Journal of Mechanical Sci-ences, 115, 339–347 (2016)

    Article  Google Scholar 

  15. SHEN, H. S., LIN, F., and XIANG, Y. Nonlinear vibration of functionally graded graphene-reinforced composite laminated beams resting on elastic foundations in thermal environments. Nonlinear Dynamics, 90(2), 899–914 (2017)

    Article  Google Scholar 

  16. FAN, Y. and WANG, H. Nonlinear dynamics of matrix-cracked hybrid laminated plates containing carbon nanotube-reinforced composite layers resting on elastic foundations. Nonlinear Dynamics, 84(3), 1181–1199 (2016)

    Article  MATH  Google Scholar 

  17. LIN, F. and XIANG, Y. Numerical analysis on nonlinear free vibration of carbon nanotube reinforced composite beams. International Journal of Structural Stability and Dynamics, 14(1), 1350056 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. WU, H., KITIPORNCHAI, S., and YANG, J. Free vibration and buckling analysis of sandwich beams with functionally graded carbon nanotube-reinforced composite face sheets. International Journal of Structural Stability and Dynamics, 15(7), 1540011 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  19. ALIBEIGLOO, A. and LIEW, K. Elasticity solution of free vibration and bending behavior of functionally graded carbon nanotube-reinforced composite beam with thin piezoelectric layers using differential quadrature method. International Journal of Applied Mechanics, 7(1), 1550002 (2015)

    Article  Google Scholar 

  20. ZHANG, L., LEI, Z., and LIEW, K. Buckling analysis of FG-CNT reinforced composite thick skew plates using an element-free approach. Composites Part B: Engineering, 75, 36–46 (2015)

    Article  Google Scholar 

  21. ZHANG, L., SONG, Z., and LIEW, K. State-space Levy method for vibration analysis of FGCNT composite plates subjected to in-plane loads based on higher-order shear deformation theory. Composite Structures, 134, 989–1003 (2015)

    Article  Google Scholar 

  22. ZHU, P., LEI, Z., and LIEW, K. M. Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Composite Structures, 94(4), 1450–1460 (2012)

    Article  Google Scholar 

  23. ZHANG, L. and LIEW, K. Large deflection analysis of FG-CNT reinforced composite skew plates resting on Pasternak foundations using an element-free approach. Composite Structures, 132, 974–983 (2015)

    Article  Google Scholar 

  24. ZHANG, L., SONG, Z., and LIEW, K. Nonlinear bending analysis of FG-CNT reinforced composite thick plates resting on Pasternak foundations using the element-free IMLS-Ritz method. Composite Structures, 128, 165–175 (2015)

    Article  Google Scholar 

  25. ZHANG, L. and LIEW, K. Geometrically nonlinear large deformation analysis of functionally graded carbon nanotube reinforced composite straight-sided quadrilateral plates. Computer Methods in Applied Mechanics and Engineering, 295, 219–239 (2015)

    Article  MathSciNet  Google Scholar 

  26. ANSARI, R., HASRATI, E., SHOJAEI, M. F., GHOLAMI, R., and SHAHABODINI, A. Forced vibration analysis of functionally graded carbon nanotube-reinforced composite plates using a numerical strategy. Physica E: Low-dimensional Systems and Nanostructures, 69, 294–305 (2015)

    Article  Google Scholar 

  27. ANSARI, R. and GHOLAMI, R. Nonlinear primary resonance of third-order shear deformable functionally graded nanocomposite rectangular plates reinforced by carbon nanotubes. Composite Structures, 154, 707–723 (2016)

    Article  Google Scholar 

  28. GUO, X. and ZHANG, W. Nonlinear vibrations of a reinforced composite plate with carbon nanotubes. Composite Structures, 135, 96–108 (2016)

    Article  Google Scholar 

  29. WANG, Z. X. and SHEN, H. S. Nonlinear vibration of nanotube-reinforced composite plates in thermal environments. Computational Materials Science, 50(8), 2319–2330 (2011)

    Article  Google Scholar 

  30. ANSARI, R., POURASHRAF, T., GHOLAMI, R., and SHAHABODINI, A. Analytical solution for nonlinear postbuckling of functionally graded carbon nanotube-reinforced composite shells with piezoelectric layers. Composites Part B: Engineering, 90, 267–277 (2016)

    Article  Google Scholar 

  31. LEI, Z., ZHANG, L., LIEW, K., and YU, J. Dynamic stability analysis of carbon nanotube-reinforced functionally graded cylindrical panels using the element-free kp-Ritz method. Composite Structures, 113, 328–338 (2014)

    Article  Google Scholar 

  32. SHEN, H. S. Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite cylindrical shells. Composites Part B: Engineering, 43, 1030–1038 (2012)

    Article  Google Scholar 

  33. ANSARI, R. and TORABI, J. Numerical study on the buckling and vibration of functionally graded carbon nanotube-reinforced composite conical shells under axial loading. Composites Part B: Engineering, 95, 196–208 (2016)

    Article  Google Scholar 

  34. WU, H., YANG, J., and KITIPORNCHAI, S. Nonlinear vibration of functionally graded carbon nanotube-reinforced composite beams with geometric imperfections. Composites Part B: Engineering, 90, 86–96 (2016)

    Article  Google Scholar 

  35. WU, H., KITIPORNCHAI, S., and YANG, J. Imperfection sensitivity of thermal post-buckling behaviour of functionally graded carbon nanotube-reinforced composite beams. Applied Mathematical Modelling, 42, 735–752 (2017)

    Article  MathSciNet  Google Scholar 

  36. WU, H., YANG, J., and KITIPORNCHAI, S. Imperfection sensitivity of postbuckling behaviour of functionally graded carbon nanotube-reinforced composite beams. Thin-Walled Structures, 108, 225–233 (2016)

    Article  Google Scholar 

  37. THANG, P. T., NGUYEN, T. T., and LEE, J. A new approach for nonlinear buckling analysis of imperfect functionally graded carbon nanotube-reinforced composite plates. Composites Part B: Engineering, 127, 166–174 (2017)

    Article  Google Scholar 

  38. PANC, V. Theories of Elastic Plates, Springer Science & Business Media, London (1975)

    Book  MATH  Google Scholar 

  39. REISSNER, E. On transverse bending of plates, including the effect of transverse shear deformation. International Journal of Solids and Structures, 11(5), 569–573 (1975)

    Article  MATH  Google Scholar 

  40. SHIMPI, R. and PATEL, H. A two variable refined plate theory for orthotropic plate analysis. International Journal of Solids and Structures, 43(22/23), 6783–6799 (2006)

    Article  MATH  Google Scholar 

  41. REDDY, J. N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, CRC Press, Boca Raton (2004)

    MATH  Google Scholar 

  42. BOUSAHLA, A. A., BENYOUCEF, S., TOUNSI, A., and MAHMOUD, S. On thermal stability of plates with functionally graded coefficient of thermal expansion. Structural Engineering and Mechanics, 60(2), 313–335 (2016)

    Article  Google Scholar 

  43. SONG, Z., ZHANG, L., and LIEW, K. Active vibration control of CNT reinforced functionally graded plates based on a higher-order shear deformation theory. International Journal of Mechanical Sciences, 105, 90–101 (2016)

    Article  Google Scholar 

  44. BELLIFA, H., BAKORA, A., TOUNSI, A., BOUSAHLA, A. A., and MAHMOUD, S. An efficient and simple four variable refined plate theory for buckling analysis of functionally graded plates. Steel and Composite Structures, 25(3), 257–270 (2017)

    Google Scholar 

  45. GHOLAMI, R. and ANSARI, R. A unified nonlocal nonlinear higher-order shear deformable plate model for postbuckling analysis of piezoelectric-piezomagnetic rectangular nanoplates with various edge supports. Composite Structures, 166, 202–218 (2017)

    Article  Google Scholar 

  46. ABDELAZIZ, H. H., MEZIANE, M. A. A., BOUSAHLA, A. A., TOUNSI, A., MAHMOUD, S., and ALWABLI, A. S. An efficient hyperbolic shear deformation theory for bending, buckling and free vibration of FGM sandwich plates with various boundary conditions. Steel and Composite Structures, 25(6), 693–704 (2017)

    Google Scholar 

  47. ESAWI, A. M. and FARAG, M. M. Carbon nanotube reinforced composites: potential and current challenges. Materials and Design, 28(9), 2394–2401 (2007)

    Article  Google Scholar 

  48. FIDELUS, J., WIESEL, E., GOJNY, F., SCHULTE, K., and WAGNER, H. Thermo-mechanical properties of randomly oriented carbon/epoxy nanocomposites. Composites Part A: Applied Sci-ence and Manufacturing, 36(11), 1555–1561 (2005)

    Article  Google Scholar 

  49. SHEN, H. S. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Composite Structures, 91(1), 9–19 (2009)

    Article  Google Scholar 

  50. ANSARI, R. and GHOLAMI, R. Size-dependent nonlinear vibrations of first-order shear deformable magneto-electro-thermo elastic nanoplates based on the nonlocal elasticity theory. International Journal of Applied Mechanics, 8(4), 1650053 (2016)

    Article  Google Scholar 

  51. ANSARI, R. and GHOLAMI, R. Surface effect on the large amplitude periodic forced vibration of first-order shear deformable rectangular nanoplates with various edge supports. Acta Astronautica, 118, 72–89 (2016)

    Article  Google Scholar 

  52. ANSARI, R., MOHAMMADI, V., SHOJAEI, M. F., GHOLAMI, R., and SAHMANI, S. On the forced vibration analysis of Timoshenko nanobeams based on the surface stress elasticity theory. Composites Part B: Engineering, 60, 158–166 (2014)

    Article  Google Scholar 

  53. SHU, C. Differential Quadrature and Its Application in Engineering, Springer Science & Business Media, London (2000)

    Book  MATH  Google Scholar 

  54. IBRAHIM, S., PATEL, B., and NATH, Y. Modified shooting approach to the non-linear periodic forced response of isotropic/composite curved beams. International Journal of Non-Linear Mechanics, 44(10), 1073–1084 (2009)

    Article  Google Scholar 

  55. KELLER, H. B. Numerical solution of bifurcation and nonlinear eigenvalue problems. Applications of Bifurcation Theory, 38, 359–384 (1977)

    MathSciNet  Google Scholar 

  56. SHEN, H. S. and ZHANG, C. L. Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite plates. Materials and Design, 31(7), 3403–3411 (2010)

    Article  Google Scholar 

  57. HAN, Y. and ELLIOTT, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Computational Materials Science, 39(2), 315–323 (2007)

    Article  Google Scholar 

  58. GRIEBEL, M. and HAMAEKERS, J. Molecular dynamics simulations of the elastic moduli of polymer-carbon nanotube composites. Computer Methods in Applied Mechanics and Engineering, 193(17), 1773–1788 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  59. SELIM, B., ZHANG, L., and LIEW, K. Vibration analysis of CNT reinforced functionally graded composite plates in a thermal environment based on Reddy’s higher-order shear deformation theory. Composite Structures, 156, 276–290 (2016)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Lahijan Branch, Islamic Azad University, Lahijan, Iran

    R. Gholami

  2. Department of Mechanical Engineering, University of Guilan, Rasht, 13756, Iran

    R. Ansari

Authors
  1. R. Gholami
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Ansari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. Gholami.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gholami, R., Ansari, R. The effect of initial geometric imperfection on the nonlinear resonance of functionally graded carbon nanotube-reinforced composite rectangular plates. Appl. Math. Mech.-Engl. Ed. 39, 1219–1238 (2018). https://doi.org/10.1007/s10483-018-2367-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-018-2367-9

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation