Skip to main content
SpringerLink
Log in

Direct numerical simulation of turbulent flows through concentric annulus with circumferential oscillation of inner wall

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

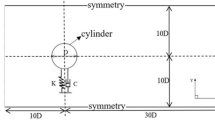
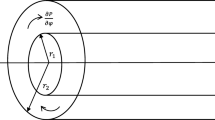
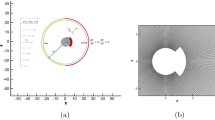
Periodic wall oscillations in the spanwise or circumferential direction can greatly reduce the friction drag in turbulent channel and pipe flows. In a concentric annulus, the constant rotation of the inner cylinder can intensify turbulence fluctuations and enhance skin friction due to centrifugal instabilities. In the present study, the effects of the periodic oscillation of the inner wall on turbulent flows through concentric annulus are investigated by the direct numerical simulation (DNS). The radius ratio of the inner to the outer cylinders is 0.1, and the Reynolds number is 2 225 based on the bulk mean velocity Um and the half annulus gap H. The influence of oscillation period is considered. It is found that for short-period oscillations, the Stokes layer formed by the circumferential wall movement can effectively inhibit the near-wall coherent motions and lead to skin friction reduction, while for long-period oscillations, the centrifugal instability has enough time to develop and generate new vortices, resulting in the enhancement of turbulence intensity and skin friction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. BRADSHAW, P. and PONTIKOS, N. S. Measurements in the turbulent boundary layer on an “infinite” swept wing. Journal of Fluid Mechanics, 159, 105–130 (1985)

    Article  Google Scholar 

  2. JUNG, W. J., MANGIAVACCHI, N., and AKHAVAN, R. Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations. Physics of Fluids A: Fluid Dynamics, 4(8), 1605–1607 (1992)

    Article  Google Scholar 

  3. AKHAVAN, R., JUNG, W. J., and MANGIAVACCHI, N. Turbulence control in wall-bounded flows by spanwise oscillations. Advances in Turbulence IV, Springer, Netherlands, 299–303 (1993)

    Google Scholar 

  4. LAADHARI, F., SKANDAJI, L., and MOREL, R. Turbulence reduction in a boundary layer by a local spanwise oscillating surface. Physics of Fluids, 6(10), 3218–3220 (1994)

    Article  Google Scholar 

  5. QUADRIO, M. and RICCO, P. Critical assessment of turbulent drag reduction through spanwise wall oscillations. Journal of Fluid Mechanics, 521, 251–271 (2004)

    Article  MATH  Google Scholar 

  6. CHOI, J. I., XU, C. X., and SUNG, H. J. Drag reduction by spanwise wall oscillation in wall-bounded turbulent flows. AIAA Journal, 40(5), 842–850 (2002)

    Article  Google Scholar 

  7. QUADRIO, M., RICCO, P., and VIOTTI, C. Streamwise-travelling waves of spanwise wall velocity for turbulent drag reduction. Journal of Fluid Mechanics, 627, 161–178 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. QUADRIO, M. and RICCO, P. The laminar generalized Stokes layer and turbulent drag reduction. Journal of Fluid Mechanics, 667, 135–157 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  9. CHOI, K. S., DEBISSCHOP, J. R., and CLAYTON, B. R. Turbulent boundary-layer control by means of spanwise-wall oscillation. AIAA Journal, 36(7), 1157–1163 (1998)

    Article  Google Scholar 

  10. CHOI, K. S. Near-wall structure of turbulent boundary layer with spanwise-wall oscillation. Physics of Fluids, 14(7), 2530–2542 (2002)

    Article  MATH  Google Scholar 

  11. CHUNG, S. Y., RHEE, G. H., and SUNG, H. J. Direct numerical simulation of turbulent concentric annular pipe flow: part 1, flow field. International Journal of Heat and Fluid Flow, 23(4), 426–440 (2002)

    Article  Google Scholar 

  12. CHUNG, S. Y. and SUNG, H. J. Large-eddy simulation of turbulent flow in a concentric annulus with rotation of an inner cylinder. International Journal of Heat and Fluid Flow, 26(2), 191–203 (2005)

    Article  MathSciNet  Google Scholar 

  13. JUNG, S. Y. and SUNG, H. J. Characterization of the three-dimensional turbulent boundary layer in a concentric annulus with a rotating inner cylinder. Physics of Fluids, 18(11), 115102 (2006)

    Article  MATH  Google Scholar 

  14. KARNIADAKIS, G. E., ISRAELI, M., and ORSZAG, S. A. High-order splitting methods for the incompressible Navier-Stokes equations. Journal of Computational Physics, 97(2), 414–443 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  15. TOUBER, E. and LESCHZINER, M. A. Near-wall streak modification by spanwise oscillatory wall motion and drag-reduction mechanisms. Journal of Fluid Mechanics, 693, 150–200 (2012)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Tsinghua University, Beijing, 100084, China

    Yichen Yao, Chunxiao Xu & Weixi Huang

Authors
  1. Yichen Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chunxiao Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Weixi Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chunxiao Xu.

Additional information

Project supported by the National Natural Science Foundation of China (No. 11490551)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yao, Y., Xu, C. & Huang, W. Direct numerical simulation of turbulent flows through concentric annulus with circumferential oscillation of inner wall. Appl. Math. Mech.-Engl. Ed. 39, 1267–1276 (2018). https://doi.org/10.1007/s10483-018-2364-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-018-2364-7

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation