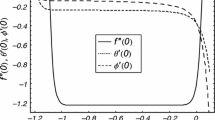
Abstract
A nonlinear flow of Jeffrey liquid with Cattaneo-Christov heat flux is investigated in the presence of nanoparticles. The features of thermophoretic and Brownian movement are retained. The effects of nonlinear radiation, magnetohydrodynamic (MHD), and convective conditions are accounted. The conversion of governing equations into ordinary differential equations is prepared via stretching transformations. The consequent equations are solved using the Runge-Kutta-Fehlberg (RKF) method. Impacts of physical constraints on the liquid velocity, the temperature, and the nanoparticle volume fraction are analyzed through graphical illustrations. It is established that the velocity of the liquid and its associated boundary layer width increase with the mixed convection parameter and the Deborah number.
Similar content being viewed by others
Abbreviations
- (U̅, V̅):
-
velocity components along x- and y- axes (m·s−1)
- X̅, Y̅ :
-
coordinates (m)
- Bi 1,Bi 2 :
-
Biot numbers
- D B :
-
Brownian diffusion coefficient (m2 · s−1)
- D T :
-
thermophoretic diffusion coefficient
- g :
-
acceleration due to gravity (m·s−1)
- Gr x :
-
local Grashof number
- h 1 :
-
heat transfer coefficient (W·m−2·K−1)
- h 2 :
-
mass transfer coefficient
- Le :
-
Lewis number
- f :
-
dimensionless velocity variable
- T̅ :
-
fluid temperature (K)
- T f :
-
temperature of fluid near wall (K)
- T ∞ :
-
ambient temperature (K)
- C̅ :
-
volumetric coefficient
- C w :
-
volume fraction of fluid near wall
- C ∞ :
-
concentration far away from surface
- c p :
-
specific heat capacity (J·kg−1·K−1)
- k :
-
thermal conductivity (W·m−1·K−1)
- k*:
-
mean absorption coefficient (m−1)
- U w :
-
= aX̅, stretching sheet velocity (m·s−1)
- a :
-
constant (s−1)
- C f :
-
skin friction coefficient
- N :
-
buoyancy parameter
- N B :
-
Brownian motion parameter
- N T :
-
thermophoretic parameter
- Nu x :
-
local Nusselt number
- Sh x :
-
local Sherwood number
- q w :
-
surface heat flux
- q m :
-
surface mass flux
- Re x :
-
local Reynolds number
- R :
-
radiation parameter
- Pr :
-
Prandtl number
- ρ :
-
density of fluid (kg·m−3)
- μ :
-
dynamic viscosity (kg·m−1·s−1)
- ν :
-
kinematic viscosity of fluid (m2 · s−1)
- σ*:
-
Stefan-Boltzman constant (W·m−2·K−4)
- α1, a 2 :
-
nonlinear convection parameters
- αm :
-
= k/(ρcp), thermal diffusivity (m2·s−1)
- β :
-
Deborah number
- β 0 :
-
linear volumetric thermal expansion coefficient
- β 1 :
-
nonlinear volumetric thermal expansion coefficient
- β 2 :
-
linear volumetric solute expansion coefficient
- β 3 :
-
nonlinear volumetric solute expansion coefficient
- θ :
-
dimensionless temperature
- θ w :
-
temperature ratio parameter
- ϕ :
-
nanoparticle volume fraction
- λ:
-
local mixed convection parameter
- λ1 :
-
ratio of relaxation/retardation time
- λ2 :
-
retardation time
- λE :
-
relaxation time of heat flux
- λC :
-
relaxation time of mass flux
- τ w :
-
wall shear stress
- τ :
-
thermophoretic parameter
- η :
-
dimensionless similarity variable
- ′:
-
derivative with respect to η
- f:
-
fluid properties at wall
- ∞:
-
fluid properties at ambient conditions
References
KOTHANDAPANI, M. and SRINIVAS, S. Peristaltic transport of a Jeffrey fluid under the effect of magnetic field in an asymmetric channel. International Journal of Non-Linear Mechanics, 43, 915–924 (2008)
SHEHZAD, S. A., ALSAADI, F. E., MONAQUEL, S. J., and HAYAT, T. Soret and Dufour effects on the stagnation point flow of Jeffrey fluid with convective boundary condition. The European Physical Journal Plus, 128, 56 (2013)
HAYAT, T., IQBAL, Z., MUSTAFA, M., and ALSAEDI, A. Unsteady flow and heat transfer of Jeffrey fluid over a stretching sheet. Thermal Science, 18, 1069–1078 (2014)
AHMAD, K. and ISHAK, A. Magnetohydrodynamic flow and heat transfer of a Jeffrey fluid towards a stretching vertical surface. Thermal Science, 21, 267–277 (2017)
AHMED, J., SHAHZAD, A., KHAN, M., and ALI, R. A note on convective heat transfer of an MHD Jeffrey fluid over a stretching sheet. AIP Advances, 5, 26–28 (2015)
HAYAT, T., WAQAS, M., SHEHZAD, S. A., and ALSAEDI, A. MHD stagnation point flow of Jeffrey fluid by a radially stretching surface with viscous dissipation and Joule heating. Journal of Hydrology and Hydromechanics, 63(4), 311–317 (2015)
KHAN, M. I., WAQAS, M., HAYAT, T., and ALSAEDI, A. Soret and Dufour effects in stretching flow of Jeffrey fluid subject to Newtonian heat and mass conditions. Results in Physics, 7, 4183–4188 (2017)
CHOI, S. U. S. Enhancing thermal conductivity of fluids with nanoparticles. Proceedings of the ASME International Mechanical Engineering Congress and Exposition, 66, 99–105 (1995)
BUONGIORNO, J. Convective transport in nanofluids. ASME Journal of Heat Transfer, 128, 240–250 (2006)
KHAN, W. A. and POP, I. Boundary-layer flow of a nanofluid past a stretching sheet. International Journal of Heat and Mass Transfer, 53, 2477–2483 (2010)
HAYAT, T., AZIZ, A., MUHAMMAD, T., and ALSAEDI, A. On magnetohydrodynamic three-dimensional flow of nanofluid over a convectively heated nonlinear stretching surface. International Journal of Heat and Mass Transfer, 100, 566–572 (2016)
MUHAMMAD, T., ALSAEDI, A., SHEHZAD, S. A., and HAYAT, T. A revised model for Darcy-Forchheimer flow of Maxwell nanofluid subject to convective boundary condition. Chinese Journal of Physics, 55(3), 963–976 (2017)
SHEIKHOLESLAMI, M., HAYAT, T., MUHAMMAD, T., and ALSAEDI, A. MHD forced convec-tion flow of nanofluid in a porous cavity with hot elliptic obstacle by means of lattice Boltzmann method. International Journal of Mechanical Sciences, 135, 532–540 (2018)
MAHANTHESH, B., GIREESHA, B. J., and GORLA, R. S. R. Heat and mass transfer effects on the mixed convective flow of chemically reacting nanofluid past a moving/stationary vertical plate. Alexandria Engineering Journal, 55, 569–581 (2016)
HAYAT, T., MUHAMMAD, T., ALSAEDI, A., and ALHUTHALI, M. S. Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. Journal of Magnetism and Magnetic Materials, 385, 222–229 (2015)
MAHANTHESH, B., GIREESHA, B. J., and GORLA, R. S. R. Mixed convection squeezing three-dimensional flow in a rotating channel filled with nanofluid. International Journal of Numerical Methods for Heat and Fluid Flow, 26, 1460–1485 (2016)
HAYAT, T., WAQAS, M., SHEHZAD, S. A., and ALSAEDI, A. A model of solar radiation and Joule heating in magnetohydrodynamic (MHD) convective flow of thixotropic nanofluid. Journal of Molecular Liquids, 215, 704–710 (2016)
MAHANTHESH, B., GIREESHA, B. J., GORLA, R. S. R., ABBASI, F. M., and SHEHZAD, S. A. Numerical solutions for magnetohydrodynamic flow of nanofluid over a bidirectional non-linear stretching surface with prescribed surface heat flux boundary. Journal of Magnetism and Magnetic Materials, 417, 189–196 (2016)
SHEIKHOLESLAMI, M., RASHIDI, M. M., and GANJI, D. D. Numerical investigation of magnetic nanofluid forced convective heat transfer in existence of variable magnetic field using two phase model. Journal of Molecular Liquids, 212, 117–126 (2015)
GIREESHA, B. J., MAHANTHESH, B., SHIVAKUMARA, I. S., and ESHWARAPPA, K. M. Melting heat transfer in boundary layer stagnation-point flow of nanofluid toward a stretching sheet with induced magnetic field. Engineering Science and Technology, An International Journal, 19(1), 313–321 (2016)
HAYAT, T., MUHAMMAD, T., QAYYUM, A., ALSAEDI, A., and MUSTAFA, M. On squeezing flow of nanofluid in the presence of magnetic field effects. Journal of Molecular Liquids, 213, 179–185 (2016)
EID, M. R., ALSAEDI, A., MUHAMMAD, T., and HAYAT, T. Comprehensive analysis of heat transfer of gold-blood nanofluid (Sisko-model) with thermal radiation. Results in Physics, 7, 4388–4393 (2017)
SAMPTH KUMAR, P. B., GIREESHA, B. J., MAHANTHESH, B., and GORLA, R. S. R. Radiative nonlinear 3D flow of ferrofluid with Joule heating, convective condition and Coriolis force. Thermal Science and Engineering Progress, 3, 88–94 (2017)
HAYAT, T., MUHAMMAD, T., SHEHZAD, S. A., and ALSAEDI, A. An analytical solution for magnetohydrodynamic Oldroyd-B nanofluid flow induced by a stretching sheet with heat generation/absorption. International Journal of Thermal Sciences, 111, 274–288 (2017)
VAJRAVELU, K., CANNON, J. R., LETO, J., SEMMOUM, R., NATHAN, N., DRAPER, M., and HAMMOCK, D. Nonlinear convection at a porous flat plate with application to heat transfer from a dike. Journal of Mathematical Analysis and Applications, 277, 609–623 (2003)
KAMESWARAN, P. K., SIBANDA, P., PARTHA, M. K., and MURTHY, P. V. S. N. Ther-mophoretic and non-linear convection in non-Darcy porous medium. Journal of Heat Transfer, 136, 042601 (2014)
SHAW, S., KAMESWARAN, P. K., and SIBANDA, P. Effects of slip on nonlinear convection in nanofluid flow on stretching surfaces. Boundary Value Problems, 2016 (2016) https://doi.org/10.1186/s13661-015-0506-2
SHAW, S., MAHANTA, G., and SIBANDA, P. Non-linear thermal convection in a Casson fluid flow over a horizontal plate with convective boundary condition. Alexandria Engineering Journal, 55, 1295–1304 (2016)
RAMREDDY, C. H. and PRADEEPA, T. Spectral quasi-linearization method for nonlinear thermal convection flow of a micropolar fluid under convective boundary condition. Nonlinear Engineering, 5, 193–204 (2016)
BANDARU, M., RASHIDI, M. M., and RAJU, S. H. Influence of nonlinear convection and ther-mophoresis on heat and mass transfer from a rotating cone to fluid flow in porous medium. Thermal Science, 21, 2781–2793 (2017)
MAHANTHESH, B., GIREESHA, B. J., SHEHZAD, S. A., ABBASI, F. M., and GORLA, R. S. R. Nonlinear three-dimensional stretched flow of an Oldroyd-B fluid with convective condition, thermal radiation, and mixed convection. Applied Mathematics and Mechanics (English Edition) 38(7), 969–980 (2017) https://doi.org/10.1007/s10483-017-2219-6
FOURIER, J. Théorie Analytique de la Chaleur, Firmin Didot Père et Fils, Paris (1822)
CATTANEO, C. Sulla conduzione del calore. Atti Semin. Mat. Fis. Univ. Modena Reggio Emilia, 3, 83–101 (1948)
CHRISTOV, C. I. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mechanics Research Communications, 36, 481–486 (2009)
STRAUGHAN, B. Thermal convection with the Cattaneo-Christov model. International Journal of Heat and Mass Transfer, 53, 95–98 (2010)
MUSTAFA, M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid. AIP Advances, 5, 047109 (2015)
KHAN, J. A., MUSTAFA, M., HAYAT, T., and ALSAEDI, A. Numerical study of Cattaneo-Christov heat flux model for viscoelastic flow due to an exponentially stretching surface. PloS One, 10, e0137363 (2015)
WAQAS, M., HAYAT, T., FAROOQ, M., SHEHZAD, S. A., and ALSAEDI, A. Cattaneo-Christov heat flux model for flow of variable thermal conductivity generalized Burgers fluid. Journal of Molecular Liquids, 220, 642–648 (2016)
HAYAT, T., AZIZ, A., MUHAMMAD, T., and ALSAEDI, A. Model and comparative study for flow of viscoelastic nanofluids with Cattaneo-Christov double diffusion. PloS One, 12, 0168824 (2017)
SHEHZAD, S. A., HAYAT, T., ALSAEDI, A., and MERAJ, M. A. Cattaneo-Christov heat and mass flux model for 3D hydrodynamic flow of chemically reactive Maxwell liquid. Applied Mathematics and Mechanics (English Edition), 38(10), 1347–1356 (2017) https://doi.org/10.1007/s10483-017-2250-6
Acknowledgements
One of the authors P. B. SAMPATH KUMAR is thankful to University Grant Commission (UGC), New Delhi, for their financial support under National Fellowship for Higher Education (NFHE) of ST students to pursue M. Phil/PhD Degree (F117.1/201516/NFST201517STKAR2228/(SAIII/Website) Dated: 06-April-2016). Also, the author B. MAHANTHESH is thankful to the Management of Christ University, Bengaluru, India, for the support through Major Research Project to accomplish this research work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sampath Kumar, P.B., Mahanthesh, B., Gireesha, B.J. et al. Quadratic convective flow of radiated nano-Jeffrey liquid subject to multiple convective conditions and Cattaneo-Christov double diffusion. Appl. Math. Mech.-Engl. Ed. 39, 1311–1326 (2018). https://doi.org/10.1007/s10483-018-2362-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-018-2362-9