Abstract
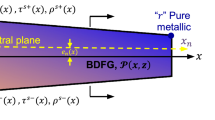
This paper focuses on the buckling behaviors of a micro-scaled bi-directional functionally graded (FG) beam with a rectangular cross-section, which is now widely used in fabricating components of micro-nano-electro-mechanical systems (MEMS/NEMS) with a wide range of aspect ratios. Based on the modified couple stress theory and the principle of minimum potential energy, the governing equations and boundary conditions for a micro-structure-dependent beam theory are derived. The present beam theory incorporates different kinds of higher-order shear assumptions as well as the two familiar beam theories, namely, the Euler-Bernoulli and Timoshenko beam theories. A numerical solution procedure, based on a generalized differential quadrature method (GDQM), is used to calculate the results of the bi-directional FG beams. The effects of the two exponential FG indexes, the higher-order shear deformations, the length scale parameter, the geometric dimensions, and the different boundary conditions on the critical buckling loads are studied in detail, by assuming that Young’s modulus obeys an exponential distribution function in both length and thickness directions. To reach the desired critical buckling load, the appropriate exponential FG indexes and geometric shape of micro-beams can be designed according to the proposed theory.
Similar content being viewed by others
References
BIAN, Z., CHEN, W., LIM, C., and ZHANG, N. Analytical solutions for single and multi-span functionally graded plates in cylindrical bending. International Journal of Solids and Structures, 42(24), 6433–6456 (2005)
WU, C., KAHN, M., and MOY, W. Piezoelectric ceramics with functional gradients: a new application in material design. Journal of the American Ceramic Society, 79(3), 809–812 (1996)
LI, C. and WENG, G. Antiplane crack problem in functionally graded piezoelectric materials. ASME Journal of Applied Mechanics, 69(4), 481–488 (2002)
BjHRIG-POLACZEK, A., FLECK, C., SPECK, T., SCH¨ULER, P., FISCHER, S., CALIARO, M., and THIELEN, M. Biomimetic cellular metals—using hierarchical structuring for energy absorption. Bioinspiration and Biomimetics, 11(4), 045002 (2016)
STUDART, A. R., ERB, R. M., and LIBANORI, R. Bioinspired Hierarchical Composites, Springer, Switzerland, 287–318 (2015)
LIN, Y., WEI, C., OLEVSKY, E., and MEYERS, M. A. Mechanical properties and the laminate structure of arapaima gigas scales. Journal of the Mechanical Behavior of Biomedical Materials, 4(7), 1145–1156 (2011)
SUN, J., THIAN, E., FUH, J., CHANG, L., HONG, G., WANG, W., TAY, B., and WONG, Y. Fabrication of bio-inspired composite coatings for titanium implants using the micro-dispensing technique. Microsystem Technologies, 18(12), 2041–2051 (2012)
LYU, C., LIM, C. W., and CHEN, W. Size-dependent elastic behavior of FGM ultra-thin films based on generalized refined theory. International Journal of Solids and Structures, 46(5), 1176–1185 (2009)
NEJAD, M. Z. and HADI, A. Eringen’s non-local elasticity theory for bending analysis of bidirectional functionally graded Euler-Bernoulli nano-beams. International Journal of Engineering Science, 106, 1–9 (2016)
KIANI, K. Stress analysis of thermally affected rotating nanoshafts with varying material properties. Acta Mechanica Sinica, 32(5), 813–827 (2016)
KIANI, K. In-plane vibration and instability of nanorotors made from functionally graded materials accounting for surface energy effect. Microsystem Technologies, 23(5), 4853–4869 (2017)
KIANI, K., GHAREBAGHI, S. A., and MEHRI, B. In-plane and out-of-plane waves in nanoplates immersed in bidirectional magnetic fields. Structural Engineering and Mechanics, 61(1), 65–76 (2017)
RAHAEIFARD, M., KAHROBAIYAN, M., and AHMADIAN, M. Sensitivity analysis of atomic force microscope cantilever made of functionally graded materials. 2009 International Design Engi- neering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, 539–544 (2009)
QUE, L., PARK, J. S., and GIANCHANDANI, Y. B. Bent-beam electrothermal actuators.: single beam and cascaded devices. Journal of Microelectromechanical Systems, 10(2), 247–254 (2001)
QUE, L., OTRADOVEC, L., OLIVER, A. D., and GIANCHANDANI, Y. B. Pulse and DCoperation lifetimes of bent-beam electrothermal actuators. The 14th IEEE International Conference on Micro Electro Mechanical Systems, IEEE, 570–573 (2001)
PARK, J. S., CHU, L. L., OLIVER, A. D., and GIANCHANDANI, Y. B. Bent-beam electrothermal actuators /: linear and rotary microengines. Journal of Microelectromechanical Systems, 10(2), 255–262 (2001)
LIN, L. and LIN, S. H. Vertically driven microactuators by electrothermal buckling effects. Sensors and Actuators A: Physical, 71(1), 35–39 (1998)
MICHAEL, A. and KWOK, C. Y. Design criteria for bi-stable behavior in a buckled multi-layered mems bridge. Journal of Micromechanics and Microengineering, 16(10), 2034–2043 (2006)
CAO, A., KIM, J., and LIN, L. Bi-directional electrothermal electromagnetic actuators. Journal of Micromechanics and Microengineering, 17(5), 975–982 (2007)
HASANYAN, D., BATRA, R., and HARUTYUNYAN, S. Pull-in instabilities in functionally graded microthermoelectromechanical systems. Journal of Thermal Stresses, 31(10), 1006–1021 (2008)
MOHAMMADI-ALASTI, B., REZAZADEH, G., BORGHEEI, A. M., MINAEI, S., and HABIBIFAR, R. On the mechanical behavior of a functionally graded micro-beam subjected to a thermal moment and nonlinear electrostatic pressure. Composite Structures, 93(6), 1516–1525 (2011)
ZHANG, J. and FU, Y. Pull-in analysis of electrically actuated viscoelastic microbeams based on a modified couple stress theory. Meccanica, 47(7), 1649–1658 (2012)
FLECK, N., MULLER, G., ASHBY, M., and HUTCHINSON, J. Strain gradient plasticity: theory and experiment. Acta Metallurgica et Materialia, 42(2), 475–487 (1994)
MCFARLAND, A. W. and COLTON, J. S. Role of material microstructure in plate stiffness with relevance to microcantilever sensors. Journal of Micromechanics and Microengineering, 15(5), 1060–1067 (2005)
HUANG, M., LI, Z., and TONG, J. The influence of dislocation climb on the mechanical behavior of polycrystals and grain size effect at elevated temperature. International Journal of Plasticity, 61, 112–127 (2014)
LIU, D., HE, Y., TANG, X., DING, H., HU, P., and CAO, P. Size effects in the torsion of microscale copper wires: experiment and analysis. Scripta Materialia, 66(6), 406–409 (2012)
DUNSTAN, D. and BUSHBY, A. The scaling exponent in the size effect of small scale plastic deformation. International Journal of Plasticity, 40, 152–162 (2013)
ERINGEN, A. Nonlocal polar elastic continua. International Journal of Engineering Science, 10(1), 1–16 (1972)
ERINGEN, A. C. Theory of Micropolar Elasticity, Springer, Switzerland, 101–248 (1999)
FLECK, N. and HUTCHINSON, J. A phenomenological theory for strain gradient effects in plasticity. Journal of the Mechanics and Physics of Solids, 41(12), 1825–1857 (1993)
YANG, F., CHONG, A., LAM, D., and TONG, P. Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures, 39(10), 2731–2743 (2002)
LIM, C., ZHANG, G., and REDDY, J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. Journal of the Mechanics and Physics of Solids, 78, 298–313 (2015)
LI, L., LI, X., and HU, Y. Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. International Journal of Engineering Science, 102, 77–92 (2016)
EBRAHIMI, F., BARATI, M. R., and DABBAGH, A. A nonlocal strain gradient theory for wave propagation analysis in temperature-dependent inhomogeneous nanoplates. International Journal of Engineering Science, 107, 169–182 (2016)
LI, C. A nonlocal analytical approach for torsion of cylindrical nanostructures and the existence of higher-order stress and geometric boundaries. Composite Structures, 118(1), 607–621 (2014)
LI, C., LIM, C. W., YU, J., and ZENG, Q. Transverse vibration of pre-tensioned nonlocal nanobeams with precise internal axial loads. Science China Technological Sciences, 54(8), 2007–2013 (2011)
LI, C., LIM, C. W., and YU, J. L. Dynamics and stability of transverse vibrations of nonlocal nanobeams with a variable axial load. Smart Materials and Structures, 20(20), 015023 (2010)
LI, C., YAO, L., CHEN, W., and LI, S. Comments on nonlocal effects in nano-cantilever beams. International Journal of Engineering Science, 87, 47–57 (2015)
LI, C. Torsional vibration of carbon nanotubes: comparison of two nonlocal models and a semicontinuum model. International Journal of Mechanical Sciences, 82(5), 25–31 (2014)
SHEN, J. P. and LI, C. A semi-continuum-based bending analysis for extreme-thin micro/nanobeams and new proposal for nonlocal differential constitution. Composite Structures, 172, 210–220 (2017)
S¸IMS¸EK, M. and REDDY, J. N. Bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory. International Journal of Engineering Science, 64, 37–53 (2013)
SALAMAT-TALAB, M., NATEGHI, A., and TORABI, J. Static and dynamic analysis of thirdorder shear deformation FGmicro beam based on modified couple stress theory. International Journal of Mechanical Sciences, 57, 63–73 (2012)
S¸IMS¸EK, M. and REDDY, J. N. A unified higher order beam theory for buckling of a functionally graded microbeam embedded in elastic medium using modified couple stress theory. Composite Structures, 101, 47–58 (2013)
NATEGHI, A., SALAMAT-TALAB, M., REZAPOUR, J., and DANESHIAN, B. Size dependent buckling analysis of functionally graded micro-beams based on modified couple stress theory. Applied Mathematical Modelling, 36(10), 4971–4987 (2012)
NGUYEN, H. X., NGUYEN, T. N., ABDEL-WAHAB, M., BORDAS, S., NGUYEN-XUAN, H., and VO, T. P. A refined quasi-3D isogeometric analysis for functionally graded microplates based on the modified couple stress theory. Computer Methods in Applied Mechanics and Engineering, 313, 904–940 (2017)
BABAEI, A., NOORANI, M. R. S., and GHANBARI, A. Temperature-dependent free vibration analysis of functionally graded micro-beams based on the modified couple stress theory. Microsys- tem Technologies, 23, 4599–4610 (2017)
WANG, Y. G., SONG, H. F., LIN, W. H., and XU, L. Large deflection analysis of functionally graded circular microplates with modified couple stress effect. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 39(3), 981–991 (2017)
AKG¨OZ, B. and CIVALEK, ¨O. Effects of thermal and shear deformation on vibration response of functionally graded thick composite microbeams. Composites Part B: Engineering, 129, 77–87 (2017)
SHENAS, A. G., ZIAEE, S., and MALEKZADEH, P. Vibrational behavior of rotating pre-twisted functionally graded microbeams in thermal environment. Composite Structures, 157, 222–235 (2016)
KAHROBAIYAN, M., RAHAEIFARD, M., TAJALLI, S., and AHMADIAN, M. A strain gradient functionally graded Euler-Bernoulli beam formulation. International Journal of Engineering Science, 52, 65–76 (2012)
SHEN, Y., CHEN, Y., and LI, L. Torsion of a functionally graded material. International Journal of Engineering Science, 109, 14–28 (2016)
SHAFIEI, N., KAZEMI, M., and GHADIRI, M. Nonlinear vibration of axially functionally graded tapered microbeams. International Journal of Engineering Science, 102, 12–26 (2016)
SHAFIEI, N., KAZEMI, M., SAFI, M., and GHADIRI, M. Nonlinear vibration of axially functionally graded non-uniform nanobeams. International Journal of Engineering Science, 106, 77–94 (2016)
KHORSHIDI, M. A., SHARIATI, M., and EMAM, S. A. Postbuckling of functionally graded nanobeams based on modified couple stress theory under general beam theory. International Jour- nal of Mechanical Sciences, 110, 160–169 (2016)
YANG, W., YANG, F., and WANG, X. Coupling influences of nonlocal stress and strain gradients on dynamic pull-in of functionally graded nanotubes reinforced nano-actuator with damping effects. Sensors and Actuators A: Physical, 248, 10–21 (2016)
EBRAHIMI, F. and BARATI, M. R. Wave propagation analysis of quasi-3D FGnanobeams in thermal environment based on nonlocal strain gradient theory. Applied Physics A, 122(9), 843–857 (2016)
BARRETTA, R., FEO, L., LUCIANO, R., DE SCIARRA, F. M., and PENNA, R. Functionally graded Timoshenko nanobeams: a novel nonlocal gradient formulation. Composites Part B: Engineering, 100, 208–219 (2016)
DEHROUYEH-SEMNANI, A. M., MOSTAFAEI, H., and NIKKHAH-BAHRAMI, M. Free flexural vibration of geometrically imperfect functionally graded microbeams. International Journal of Engineering Science, 105, 56–79 (2016)
LI, L., HU, Y., and LING, L. Flexural wave propagation in small-scaled functionally graded beams via a nonlocal strain gradient theory. Composite Structures, 133, 1079–1092 (2015)
LI, X., LI, L., HU, Y., DENG, W., and DING, Z. A refined nonlocal strain gradient theory for assessing scaling-dependent vibration behavior of microbeams. International Journal of Mechanical, Aerospace, Industrial, Mechatronic and Manufacturing Engineering, 11(3), 517–527 (2017)
TADI-BENI, Y. Size-dependent electromechanical bending, buckling, and free vibration analysis of functionally graded piezoelectric nanobeams. Journal of Intelligent Material Systems and Struc- tures, 27(16), 2199–2215 (2016)
RAZAVI, H., BABADI, A. F., and TADI-BENI, Y. Free vibration analysis of functionally graded piezoelectric cylindrical nanoshell based on consistent couple stress theory. Composite Structures, 160, 1299–1309 (2017)
TADI-BENI, Y., MEHRALIAN, F., and ZEIGHAMPOUR, H. The modified couple stress functionally graded cylindrical thin shell formulation. Mechanics of Advanced Materials and Structures, 23(7), 791–801 (2016)
TADI-BENI, Y. and MEHRALIAN, F. The effect of small scale on the free vibration of functionally graded truncated conical shells. Journal of Mechanics of Materials and Structures, 11(2), 91–112 (2016)
MEHRALIAN, F. and TADI-BENI, Y. Size-dependent torsional buckling analysis of functionally graded cylindrical shell. Composites Part B: Engineering, 94, 11–25 (2016)
WANG, X. and LI, S. Free vibration analysis of functionally graded material beams based on Levinson beam theory. Applied Mathematics and Mechanics (English Edition), 37(7), 861–878 (2016) https://doi.org/10.1007/s10483-016-2094-9
SETOODEH, A., REZAEI, M., and ZENDEHDEL-SHAHRI, M. R. Linear and nonlinear torsional free vibration of functionally graded micro/nano-tubes based on modified couple stress theory. Applied Mathematics and Mechanics (English Edition), 37(6), 725–740 (2016) https://doi.org/10.1007/s10483-016-2085-6
WAN, Z. and LI, S. Thermal buckling analysis of functionally graded cylindrical shells. Applied Mathematics and Mechanics (English Edition), 38(8), 1059–1070 (2017) https://doi.org/10.1007/s10483-017-2225-7
KOLAHCHI, R. and MONIRI-BIDGOLI, A. M. Size-dependent sinusoidal beam model for dynamic instability of single-walled carbon nanotubes. Applied Mathematics and Mechanics (English Edition), 37(2), 265–274 (2016) https://doi.org/10.1007/s10483-016-2030-8
LI, X., LI, L., HU, Y., DING, Z., and DENG, W. Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Composite Structures, 165, 250–265 (2017)
LI, L. and HU, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. International Journal of Engineering Science, 107, 77–97 (2016)
LI, L. and HU, Y. Post-buckling analysis of functionally graded nanobeams incorporating nonlocal stress and microstructure-dependent strain gradient effects. International Journal of Mechanical Sciences, 120, 159–170 (2017)
LI, L. and HU, Y. Torsional vibration of bi-directional functionally graded nanotubes based on non-local elasticity theory. Composite Structures, 172, 242–250 (2017)
STEINBERG, M. A. Materials for aerospace. Scientific American, 255(4), 66–72 (1986)
LYU, C., CHEN,W., XU, R., and LIM, C.W. Semi-analytical elasticity solutions for bi-directional functionally graded beams. International Journal of Solids and Structures, 45(1), 258–275 (2008)
NEMAT-ALLA, M. and NODA, N. Edge crack problem in a semi-infinite FGM plate with a bi-directional coeffcient of thermal expansion under two-dimensional thermal loading. Acta Me- chanica, 144(3), 211–229 (2000)
NEMAT-ALLA, M. Reduction of thermal stresses by developing two-dimensional functionally graded materials. International Journal of Solids and Structures, 40(26), 7339–7356 (2003)
NEMAT-ALLA, M., AHMED, K. I., and HASSAB-ALLAH, I. Elastic-plastic analysis of twodimensional functionally graded materials under thermal loading. International Journal of Solids and Structures, 46(14), 2774–2786 (2009)
LEZGY-NAZARGAH, M. Fully coupled thermo-mechanical analysis of bi-directional FGM beams using NURBS isogeometric finite element approach. Aerospace Science and Technology, 45, 154–164 (2015)
CHO, J. and HA, D. Optimal tailoring of 2D volume-fraction distributions for heat-resisting functionally graded materials using FDM. Computer Methods in Applied Mechanics and Engineering, 191(29), 3195–3211 (2002)
QIAN, L. and BATRA, R. Design of bidirectional functionally graded plate for optimal natural frequencies. Journal of Sound and Vibration, 280(1), 415–424 (2005)
NIE, G. and ZHONG, Z. Axisymmetric bending of two-directional functionally graded circular and annular plates. Acta Mechanica Solida Sinica, 20(4), 289–295 (2007)
NIE, G. and ZHONG, Z. Dynamic analysis of multi-directional functionally graded annular plates. Applied Mathematical Modelling, 34(3), 608–616 (2010)
LYU, C., LIM, C. W., and CHEN, W. Semi-analytical analysis for multi-directional functionally graded plates: 3D elasticity solutions. International Journal for Numerical Methods in Engineer- ing, 79(1), 25–44 (2009)
DENG, H. and CHENG, W. Dynamic characteristics analysis of bi-directional functionally graded Timoshenko beams. Composite Structures, 141, 253–263 (2016)
PYDAH, A. and BATRA, R. Shear deformation theory using logarithmic function for thick circular beams and analytical solution for bi-directional functionally graded circular beams. Composite Structures, 172, 45–60 (2017)
PYDAH, A. and SABALE, A. Static analysis of bi-directional functionally graded curved beams. Composite Structures, 160, 867–876 (2017)
NGUYEN, D. K., NGUYEN, Q. H., TRAN, T. T., and BUI, V. T. Vibration of bi-dimensional functionally graded Timoshenko beams excited by a moving load. Acta Mechanica, 228(1), 145–155 (2017)
S¸IMS¸EK, M. Buckling of Timoshenko beams composed of two-dimensional functionally graded material (2D-FGM) having different boundary conditions. Composite Structures, 149, 304–314 (2016)
S¸IMS¸EK, M. Bi-directional functionally graded materials (BDFGMs) for free and forced vibration of Timoshenko beams with various boundary conditions. Composite Structures, 133, 968–978 (2015)
NEJAD, M. Z., HADI, A., and RASTGOO, A. Buckling analysis of arbitrary two-directional functionally graded Euler-Bernoulli nano-beams based on nonlocal elasticity theory. International Journal of Engineering Science, 103, 1–10 (2016)
NEJAD, M. Z. and HADI, A. Non-local analysis of free vibration of bi-directional functionally graded Euler-Bernoulli nano-beams. International Journal of Engineering Science, 105, 1–11 (2016)
SHAFIEI, N. and KAZEMI, M. Buckling analysis on the bi-dimensional functionally graded porous tapered nano-/micro-scale beams. Aerospace Science and Technology, 66, 1–11 (2017)
CHEN, X., MA, L., ZHENG, Y., LI, X., and LEE, D. W. The influences of transverse loads on electrothermal post-buckling microbeams. Journal of Micromechanics and Microengineering, 22(1), 015011 (2011)
REDDY, J. N. A simple higher-order theory for laminated composite plates. Journal of Applied Mechanics, 51(4), 745–752 (1985)
TOURATIER, M. An effcient standard plate theory. International Journal of Engineering Science, 29(8), 901–916 (1991)
KARAMA, M., AFAQ, K., and MISTOU, S. Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. International Journal of Solids and Structures, 40(6), 1525–1546 (2003)
SOLDATOS, K. P. A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mechanica, 94, 195–220 (1992)
AYDOGDU, M. A new shear deformation theory for laminated composite plates. Composite Struc- tures, 89(1), 94–101 (2009)
TOUNSI, A., SEMMAH, A., and BOUSAHLA, A. A. Thermal buckling behavior of nanobeams using an effcient higher-order nonlocal beam theory. Journal of Nanomechanics and Microme- chanics, 3(3), 37–42 (2013)
BOURADA, M., KACI, A., HOUARI,M. S. A., and TOUNSI, A. A new simple shear and normal deformations theory for functionally graded beams. Steel and Composite Structures, 18(2), 409–423 (2015)
ZEMRI, A., HOUARI, M. S. A., BOUSAHLA, A. A., and TOUNSI, A. A mechanical response of functionally graded nanoscale beam: an assessment of a refined nonlocal shear deformation theory beam theory. Structural Engineering and Mechanics, 54(4), 693–710 (2015)
EBRAHIMI, F. and BARATI, M. R. A nonlocal higher-order refined magneto-electro-viscoelastic beam model for dynamic analysis of smart nanostructures. International Journal of Engineering Science, 107, 183–196 (2016)
NGUYEN, T. K., NGUYEN, T. P., VO, T. P., and THAI, H. T. Vibration and buckling analysis of functionally graded sandwich beams by a new higher-order shear deformation theory. Composites Part B: Engineering, 76(3), 273–285 (2015)
LI, L. and HU, Y. Buckling analysis of size-dependent nonlinear beams based on a nonlocal strain gradient theory. International Journal of Engineering Science, 97, 84–94 (2015)
ZHU, X. and LI, L. Twisting statics of functionally graded nanotubes using Eringens nonlocal integral model. Composite Structures, 178, 87–96 (2017)
DELALE, F. and ERDOGAN, F. The crack problem for a nonhomogeneous plane. Journal of Applied Mechanics, 50(3), 609–614 (1983)
ALSHORBAGY, A. E., ELTAHER, M., and MAHMOUD, F. Free vibration characteristics of a functionally graded beam by finite element method. Applied Mathematical Modelling, 35(1), 412–425 (2011)
ZHAO, L., CHEN, W., and LYU, C. Symplectic elasticity for bi-directional functionally graded materials. Mechanics of Materials, 54, 32–42 (2012)
SURESH, S. Graded materials for resistance to contact deformation and damage. Science, 292(5526), 2447–2451 (2001)
SURESH, S., GIANNAKOPOULOS, A., and ALCALA, J. Spherical indentation of compositionally graded materials: theory and experiments. Acta Materialia, 45(4), 1307–1321 (1997)
LI, L., LI, X., and HU, Y. Nonlinear bending of a two-dimensionally functionally graded beam. Composite Structures, 184, 1049–1061 (2018)
LI, L. and HU, Y. Torsional statics of two-dimensionally functionally graded microtubes. Mechanics of Advanced Materials and Structures, 1–13 (2017) https://doi.org/10.1080/15376494.2017.1400617
ASKES, H. and AIFANTIS, E. C. Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. International Journal of Solids and Structures, 48(13), 1962–1990 (2011)
JONES, R. M. Buckling of Bars, Plates, and Shells, Bull Ridge, Blacksburg (2006)
WU, T. Y. and LIU, G. R. A differential quadrature as a numerical method to solve differential equations. Computational Mechanics, 24(3), 197–205 (1999)
WU, T. Y. and LIU, G. R. Application of generalized differential quadrature rule to sixth-order differential equations. Communications in Numerical Methods in Engineering, 16(11), 777–784 (2000)
SUI, S., CHEN, L., LI, C., and LIU, X. Transverse vibration of axially moving functionally graded materials based on Timoshenko beam theory. Mathematical Problems in Engineering, 2015, 391452 (2015)
SHU, C. and RICHARDS, B. E. Application of generalized differential quadrature to solve twodimensional incompressible Navier-Stokes equations. International Journal for Numerical Methods in Fluids, 15(7), 791–798 (1992)
QUAN, J. R. and CHANG, C. T. New insights in solving distributed system equations by the quadrature method II: numerical experiments. Computers and Chemical Engineering, 13(9), 1017–1024 (1989)
Author information
Authors and Affiliations
Corresponding author
Additional information
Citation: LI, X. B., LI, L., and HU, Y. J. Instability of functionally graded micro-beams via microstructure-dependent beam theory. Applied Mathematics and Mechanics (English Edition), 39(7), 923–952 (2018) https://doi.org/10.1007/s10483-018-2343-8
Project supported by the National Natural Science Foundation of China (Nos. 51375184 and 51605172) and the Fundamental Research Funds for the Central Universities (No. 2015MS014)
Rights and permissions
About this article
Cite this article
Li, X., Li, L. & Hu, Y. Instability of functionally graded micro-beams via micro-structure-dependent beam theory. Appl. Math. Mech.-Engl. Ed. 39, 923–952 (2018). https://doi.org/10.1007/s10483-018-2343-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-018-2343-8