Skip to main content
SpringerLink
Log in

Approximate solutions for the problem of liquid film flow over an unsteady stretching sheet with thermal radiation and magnetic field

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

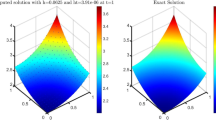
The proposed method is based on replacement of the unknown function by a truncated series of the shifted Legendre polynomial expansion. An approximate formula of the integer derivative is introduced. Special attention is given to study the convergence analysis and derive an upper bound of the error for the presented approximate formula. The introduced method converts the proposed equation by means of collocation points to a system of algebraic equations with shifted Legendre coefficients. Thus, after solving this system of equations, the shifted Legendre coefficients are obtained. This efficient numerical method is used to solve the system of ordinary differential equations which describe the thin film flow and heat transfer with the effects of the thermal radiation, magnetic field, and slip velocity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Wang, C. Y. Liquid film on an unsteady stretching surface. Quarterly of Applied Mathematics, 48, 601-610 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  2. Usha, R. and Sridharan, R. The axis-symmetric motion of a liquid film on an unsteady stretching surface. Journal of Fluids Engineering, 117, 81᾿5 (1995)

    Article  Google Scholar 

  3. Wang, C. Analytic solutions for a liquid thin film on an unsteady stretching surface. Heat and Mass Transfer, 42, 759᾿66 (2006)

    Article  Google Scholar 

  4. Liu, I. C. and Andersson, H. I. Heat transfer in a liquid film on an unsteady stretching sheet. International Journal of Thermal Sciences, 47, 766᾿72 (2008)

    Article  Google Scholar 

  5. Santra, B. and Dandapat, B. S. Unsteady thin-film flow over a heated stretching sheet. International Journal of Heat and Mass Transfer, 52, 1965᾿970 (2009)

    Article  MATH  Google Scholar 

  6. Noor, N. F. M., Abdulaziz, O., and Hashim, I. MHD flow and heat transfer in a thin liquid film on an unsteady stretching sheet by the homotopy analysis method. International Journal for Numerical Methods in Fluids, 63, 357᾿73 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Andersson, H. I., Aarseth, J. B., and Dandapat, B. S. Heat transfer in a liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 43, 69᾿4 (2000)

    Article  MATH  Google Scholar 

  8. Dandapat, B. S., Santra, B., and Andersson, H. I. Thermo-capillarity in a liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 46, 3009᾿015 (2003)

    Article  MATH  Google Scholar 

  9. Dandapat, B. S., Santra, B., and Vajravelu, K. The effects of variable fluid properties and thermocapillarity on the flow of a thin film on an unsteady stretching sheet. International Journal of Heat and Mass Transfer, 50, 991᾿96 (2007)

    Article  MATH  Google Scholar 

  10. Dandapat, B. S. and Maity, S. Flow of a thin liquid film on an unsteady stretching sheet. Physics of Fluids, 18, 102101᾿02107 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  11. Noor, N. F. M. and Hashim, I. Thermo-capillarity and magnetic field effects in a thin liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 53, 2044᾿051 (2010)

    Article  MATH  Google Scholar 

  12. Khader, M. M. On the numerical solution and convergence study for system of non-linear fractional diffusion equations. Canadian Journal of Physics, 92(12), 1658᾿666 (2014)

    Article  Google Scholar 

  13. Bell, W. W. Special Functions for Scientists and Engineers, Butler and Tanner Ltd., Frome and London (1968)

    MATH  Google Scholar 

  14. Sweilam, N. H., Khader, M. M., and Mahdy, A. M. S. Numerical studies for fractional-order logistic differential equation with two different delays. Journal of Applied Mathematics, 2012, 1᾿4 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Khader, M. M. and Hendy, A. S. A new Legendre computational matrix method: an application for solving the high order fractional differential equations. Walailak Journal of Science and Technology, 11(4), 289᾿05 (2014)

    Google Scholar 

  16. Khader, M. M. Shifted Legendre collocation method for the flow and heat transfer due to a stretching sheet embedded in a porous medium with variable thickness, variable thermal conductivity and thermal radiation. Mediterranean Journal of Mathematics, 13(4), 2319᾿336 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, College of Science, Al-Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, 11623, Saudi Arabia

    M. M. Khader

  2. Department of Mathematics, Faculty of Science, Benha University, Benha, 13511, Egypt

    M. M. Khader

Authors
  1. M. M. Khader
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. M. Khader.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khader, M.M. Approximate solutions for the problem of liquid film flow over an unsteady stretching sheet with thermal radiation and magnetic field. Appl. Math. Mech.-Engl. Ed. 39, 867–876 (2018). https://doi.org/10.1007/s10483-018-2340-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-018-2340-9

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation