Skip to main content
SpringerLink
Log in

Rayleigh-type wave propagation in incompressible visco-elastic media under initial stress

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

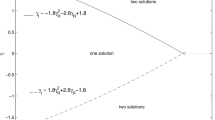
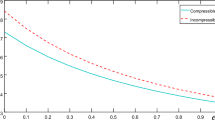
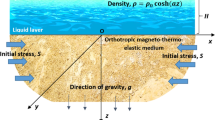
Propagation of Rayleigh-type surface waves in an incompressible visco-elastic material over incompressible visco-elastic semi-infinite media under the effect of initial stresses is discussed. The dispersion equation is determined to study the effect of different types of parameters such as inhomogeneity, initial stress, wave number, phase velocity, damping factor, visco-elasticity, and incompressibility on the Rayleigh-type wave propagation. It is found that the affecting parameters have a significant effect on the wave propagation. Cardano’s and Ferrari’s methods are deployed to estimate the roots of differential equations associated with layer and semi-infinite media. The MATHEMATICA software is applied to explicate the effect of these parameters graphically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Biot, M. A. Mechanics of Incremental Deformations, John Wiley, New York (1965)

    Google Scholar 

  2. Achenbach, J. Wave Propagation in Elastic Solids, Elsevier, New York (1973)

    MATH  Google Scholar 

  3. Stoneley, R. The transmission of Rayleigh waves in a heterogeneous medium. Geophysical Journal International, 3, 222–232 (1934)

    Article  MATH  Google Scholar 

  4. Dutta, S. Rayleigh wave propagation in a two-layer anisotropic media. Pure and Applied Geophysics, 60, 51–60 (1965)

    Article  MATH  Google Scholar 

  5. Chattopadhyay, A. Propagation of SH waves in a viscoelastic medium due to irregularity in the crustal layer. Bulletin of Calcutta Mathematical Society, 70, 303–316 (1978)

    MATH  Google Scholar 

  6. Dey, S., Chattopadhyay, A., and Chakraborty, M. Effect of initial stresses on reflection on transmission of seismic-wave at the Earth core-mantle boundary. Archive of Mechanics, 34, 61–72 (1982)

    MATH  Google Scholar 

  7. Pal, A. K. and Chattopadhyay, A. The reflection phenomena of plane waves at a free boundary in a prestressed elastic half-space. Journal of Acoustical Society of America, 76, 924–925 (1984)

    Article  Google Scholar 

  8. Chattopadhyay, A., Mahata, N. P., and Keshri, A. Rayleigh waves in a medium under initial stresses. Acta Geophysica Polonica, 34, 57–62 (1986)

    Google Scholar 

  9. Sharma, M. D. and Gogna, M. L. Seismic wave propagation in a viscoelastic porous solid saturated by viscous liquid. Pure and Applied Geophysics, 135(3), 383–400 (1991)

    Article  Google Scholar 

  10. Fu, Y. and Rogerson, G. A. A nonlinear analysis of instability of a pre-stressed incompressible elastic plate. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 446, 233–254 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  11. Rogerson, G. A. and Fu, Y. B. An asymptotic analysis of the dispersion relation of a pre-stressed incompressible elastic plate. Acta Mechanica, 111, 59–74 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  12. Abd-Alla, A. M., Hammad, H. A. H., and Abo-Dahab, S. M. Rayleigh waves in a magneto elastic half-space of orthotropic material under influence of initial stress and gravity field. Applied Mathematics and Computation, 154, 583–597 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Abd-Alla, A. M., Abo-Dahab, S. M., Hammad, H. A., and Mahmoud, S. R. On generalized magneto-thermoelastic Rayleigh waves in a granular medium under the influence of a gravity field and initial stress. Journal of Vibration and Control, 17, 115–128 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  14. Abd-Alla, A. M., Abo-Dahab, S. M., and Al-Thamali, T. A. Propagation of Rayleigh waves in a rotating orthotropic material elastic half-space under initial stress and gravity. Journal of Mechanical Science and Technology, 26, 2815–2823 (2012)

    Article  Google Scholar 

  15. Sharma, M. D. Rayleigh waves in dissipative poro-viscoelastic media. Bulletin of the Seismological Society of America, 102, 2468–2483 (2012)

    Article  Google Scholar 

  16. Sharma, M. D. Propagation and attenuation of Rayleigh waves in generalized thermo elastic media. Journal of Seismology, 18, 61–79 (2014)

    Article  Google Scholar 

  17. Ahmed, S. M. and Abo-Dahab, S. M. Influence of initial stress and gravity field on propagation of Rayleigh and Stoneley waves in a thermoelastic orthotropic granular medium. Mathematical Problems in Engineering, 2012, 245965 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  18. Ogden, R. W. and Singh, B. The effect of rotation and initial stress on the propagation of waves in a transversely isotropic elastic solid. Wave Motion, 51, 1108–1126 (2014)

    Article  MathSciNet  Google Scholar 

  19. Wang, Y. Z., Li, F. M., Kishimoto, K., Wang, Y. S., and Huang, W. H. Band gaps of elastic waves in three-dimensional piezoelectric phononic crystals with initial stress. European Journal of Mechanics-A/Solids, 29, 182–189 (2010)

    Article  Google Scholar 

  20. Wang, Y., Li, F., Kishimoto, K., Wang, Y., and Huang, W. Wave localization in randomly disordered periodic piezoelectric rods with initial stress. Acta Mechanica Solida Sinica, 21, 529–535 (2008)

    Article  Google Scholar 

  21. Chatterjee, M., Dhua, S., and Chattopadhyay, A. Response of moving load due to irregularity in slightly compressible, finitely deformed elastic media. Mechanics Research Communications, 66, 49–59 (2015)

    Article  Google Scholar 

  22. Chatterjee, M., Dhua, S., and Chattopadhyay, A. Propagation of shear waves in viscoelastic heterogeneous layer overlying an initially stressed half space. Journal of Physics: Conference Series, 662, 012001 (2015)

    Google Scholar 

  23. Dhua, S. and Chattopadhyay, A. Wave propagation in heterogeneous layers of the Earth. Waves in Random and Complex Media, 26, 626–641 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Kumari, P., Modi, C., and Sharma, V. K. Torsional waves in a magneto-viscoelastic layer over an inhomogeneous substratum. The European Physical Journal Plus, 131, 263 (2016)

    Article  Google Scholar 

  25. Kumari, P., Sharma, V. K., and Modi, C. Modeling of magnetoelastic shear waves due to point source in a viscoelastic crustal layer over an inhomogeneous viscoelastic half space. Waves in Random and Complex Media, 26, 101–120 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  26. Khurana, A. and Tomar, S. K. Rayleigh-type waves in nonlocal micropolar solid half-space. Ultrasonics, 73, 162–168 (2017)

    Article  Google Scholar 

  27. Chatterjee, M. and Chattopadhyay, A. Propagation, reflection and transmission of SH-waves in slightly compressible, finitely deformed elastic media. Applied Mathematics and Mechanics (English Edition), 36(8), 1045–1056 (2015) https://doi.org/10.1007/s10483-015-1961-7

    Article  MathSciNet  MATH  Google Scholar 

  28. Gubbins, D. Seismology and Plate Tectonics, Cambridge University Press, Cambridge (1990)

    Google Scholar 

  29. Caloi, P. Comportement des ondes de Rayleigh dans unmilieu firmoelastique indefini (in French). Publications du Bureau Central Séismoloqique International: Travaux Scientifiques Série A, 17, 89–108 (1948)

    MathSciNet  Google Scholar 

Download references

Acknowledgements

Ms. P. SINGH conveys her sincere thanks to Indian Institute of Technology (Indian School of Mines), Dhanbad, India for providing Junior Research Fellowship.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Indian Institute of Technology (ISM), Dhanbad, 826007, India

    P. Singh, A. Chattopadhyay & A. K. Singh

Authors
  1. P. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Chattopadhyay
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. K. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. Singh.

Additional information

Citation: Singh, P., Chattopadhyay, A., and Singh, A. K. Rayleigh-type wave propagation in incompressible visco-elastic media under initial stress. Applied Mathematics and Mechanics (English Edition), 39(3), 317–334 (2018) https://doi.org/10.1007/s10483-018-2306-9

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Singh, P., Chattopadhyay, A. & Singh, A.K. Rayleigh-type wave propagation in incompressible visco-elastic media under initial stress. Appl. Math. Mech.-Engl. Ed. 39, 317–334 (2018). https://doi.org/10.1007/s10483-018-2306-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-018-2306-9

Keywords

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation