Skip to main content
SpringerLink
Log in

Interaction between compressibility and particulate suspension on peristaltically driven flow in planar channel

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

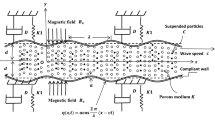
The peristaltic pumping of a viscous compressible liquid mixed with rigid spherical particles of the same size in a channel is theoretically investigated. The momentum equations for the compressible flow are solved with a perturbation analysis. The analysis is carried out by duly accounting for the nonlinear convective acceleration terms for the fluid part on the wavy wall. The zeroth-order terms yield the Poiseuille flow, and the first-order terms give the Orr-Sommerfeld equation. The explicit expression for the net axial velocity is derived. The effects of the embedded parameters on the axial fluid velocity are studied through different engineering applications. The features of the flow characteristics are analyzed and discussed in detail. The obtained results are evaluated for various parameters associated with the blood flow in the blood vessels with diameters less than 5 500 mm, whereas the particle diameter has been taken to be 8 mm. This study provides a scope to evaluate the effect of the theory of two-phase flow characteristics with compressible fluid problems, and is helpful for understanding the role of engineering applications of pumping solid-fluid mixture by peristaltically driven motion.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

2d :

mean width 2d

(u f, v f):

liquid phase velocities

x :

Cartesian coordinate measuring the direction of the wave propagation

y :

Cartesian coordinate measuring the direction normal to the mean position of the channel walls

C :

volume fraction density of the particles

(u p :

vp), particulate phase velocities

p :

pressure

S :

drag coefficient of interaction for the force exerted by one phase on the other

k*:

compressibility of the liquid

a 0 :

radius of the particle

T :

absolute temperature (K)

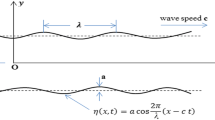
a :

amplitude

c :

wave speed

Re :

suspension Reynolds number

M, N :

suspension parameters

Z(y):

mean-velocity perturbation function

〈Vfx〉:

net time axial velocity of the fluid phase

f w :

frequency of wave

V fx :

dimensional net axial velocity of the fluid phase

Δp :

excess pressure

c o :

speed of sound in the oil

P :

average power output generated at the acoustic source

G :

shear modulus of the porous medium

D :

distensibility of the channel

f :

frequency of the acoustic source

ρ f :

actual density of the materials constituting liquid

ρ p :

actual density of the particulate phase

λ:

wavelength

(1 − C)ρ f :

liquid phase density

Cρp :

particulate phase density

μ s(C):

particle liquid mixture viscosity, i.e., effective viscosity of the suspension

ρ :

constant density at the reference pressure

μ 0 :

fluid viscosity

μ :

viscosity of the liquid

η :

transverse displacement of the wall

χ :

compressibility number

α :

wave number

ε :

amplitude ratio

References

  1. Latham, T. W. Fluid Motion in a Peristaltic Pump, M. Sc. dissertation, Massachusetts Institute of Technology, Cambridge (1966)

    Google Scholar 

  2. Rath, H. J. Peristaltische Stromungen, Springer, Berlin (1980)

    Book  MATH  Google Scholar 

  3. Srivastava, L. M. and Srivastava, V. P, Peristaltic transport of blood: Casson model-II. Journal of Biomechanics 17, 821–830 (1984)

    Article  Google Scholar 

  4. Srivastava, L. M. and Srivastava, V. P, Interaction of peristaltic flow with pulsatile flow in a circular cylindrical tube. Journal of Biomechanical Engineering 18, 247–253 (1985)

    Article  Google Scholar 

  5. Srivastava, L. M. and Srivastava, V. P, Peristaltic transport of a particle-fluid suspension. Journal of Biomechanical Engineering 111, 157–65 (1989)

    Article  Google Scholar 

  6. Srivastava, L. M. and Srivastava, V. P, Effects of poiseuille flow on peristaltic transport of a particulate suspension. Zeitschrift für Angowandte Mathematik und Physik 46, 655–679 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  7. Srivastava, V. E. and Saxena, M. A, Two-fluid model of non-Newtonian blood flow induced by peristaltic waves. Rheologica Acta 34, 406–414 (1995)

    Article  Google Scholar 

  8. Hung, T. K. and Brown, T. D, Solid-particle motion in two-dimensional peristaltic flows. Journal of Fluid Mechanics 73, 77–96 (1976)

    Article  Google Scholar 

  9. Mekheimer, K. S., El-Shehawey, E. F., and Elaiw, A. M, Peristaltic motion of a particle-fluid suspension in a planar channel. International Journal of Theoretical Physics 37, 2895–2920 (1998)

    Article  MATH  Google Scholar 

  10. El-Misery, A. M., El-Shehawey, E. F., and Hakeem, A. A, Peristaltic motion of an incompressible generalized Newtonian fluid in a planar channel. Journal of Physical Society 65, 3524–3529 (1996)

    Article  Google Scholar 

  11. Aarts, A. C. T. and Ooms, G, Net Flow of compressible viscous liquids induced by traveling waves in porous media. Journal of Engineering Mathematics 34, 435–450 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  12. Antanovskii, L. K. and Ramkissoon, H, Long-wave peristaltic transport of a compressible viscous fluid in a finite pipe subject to a time dependent pressure drop. Fluid Dynamics Research 19, 115–123 (1997)

    Article  Google Scholar 

  13. Tsiklauri, D. and Beresenev, I, Non-Newtonian effects in the peristaltic flow of a Maxwell fluid. Physics Review E 64, 0363031–0363035 (2001)

    Article  Google Scholar 

  14. Castulik, P, The compressible boundary layer and the Boltzmann equation. The compressible boundary layer and the Boltzmann equation 15, 17–23 (2002)

    MathSciNet  MATH  Google Scholar 

  15. Kawashita, M, On global solutions of Cauchy problems for compressible Navier-Stokes equations. On global solutions of Cauchy problems for compressible Navier-Stokes equations 48, 1087–1105 (2002)

    MathSciNet  MATH  Google Scholar 

  16. Eldesoky, I. M. and Mousa, A. A. Peristaltic pumping of fluid in cylindrical tube and its applications in the field of aerospace. 13th International Conference on Aerospace Sciences and Aviation Technology, Military Technical College, Cairo, 1–14 (2009)

    Google Scholar 

  17. Eldesoky, I. M, Influence of slip condition on pristaltic transport of a compressible Maxwell fluid through porous medium in a tube. Influence of slip condition on pristaltic transport of a compressible Maxwell fluid through porous medium in a tube 8, 99–117 (2012)

    Google Scholar 

  18. Mekheimer, K. S. and Abdel-Wahab, A. N, Net annulus flow of a compressible viscous liquid with peristalsis. Net annulus flow of a compressible viscous liquid with peristalsis 25, 660–669 (2012)

    Google Scholar 

  19. Mekheimer, K. S., El-Komy, S. R., and Abdelsalam, S. I, Simultaneous effects of magnetic field and space porosity on compressible Maxwell fluid transport induced by a surface acoustic wave in a micro-channel. Simultaneous effects of magnetic field and space porosity on compressible Maxwell fluid transport induced by a surface acoustic wave in a micro-channel 22, 1247021–12470210 (2013)

    Google Scholar 

  20. Felderhof, B. U, Dissipation in peristaltic pumping of a compressible viscous fluid through a planar duct or a circular tube. Dissipation in peristaltic pumping of a compressible viscous fluid through a planar duct or a circular tube 83, 0463101–0463106 (2011)

    Google Scholar 

  21. Elshehawey, E. F., El-Saman, E. R., El-Shahed, M., and Dagher, M, Peristaltic transport of a compressible viscous liquid through a tapered pore. Peristaltic transport of a compressible viscous liquid through a tapered pore 169, 526–543 (2005)

    MathSciNet  MATH  Google Scholar 

  22. Hayat, T., Ali, N., and Asghar, S, An analysis of peristaltic transport for flow of a Jeffrey fluid. An analysis of peristaltic transport for flow of a Jeffrey fluid 193, 101–112 (2007)

    MATH  Google Scholar 

  23. El-Shehawy, E. F., El-Dabe, N. T., and Eldesoky, I. M, Slip effects on the peristaltic flow of a non-Newtonian Maxwellian fluid. Slip effects on the peristaltic flow of a non-Newtonian Maxwellian fluid 186, 141–159 (2006)

    MATH  Google Scholar 

  24. Fung, Y. C. and Yih, C. S, Peristaltic transport. Peristaltic transport 35, 669–675 (1968)

    MATH  Google Scholar 

  25. Drew, D. A, Stability of a Stokes layer of a dusty gas. Stability of a Stokes layer of a dusty gas 22, 2081–2086 (1979)

    MathSciNet  MATH  Google Scholar 

  26. Srivastava, L. M. and Srivastava, V. P, On two-phase model of pulsatile blood flow with entrance effects. On two-phase model of pulsatile blood flow with entrance effects 20, 761–777 (1983)

    Google Scholar 

  27. Anderson, J. D. Modern Compressible Flow: With Historical Perspective, McGraw Hill Higher Company, New York (1990)

    Google Scholar 

  28. Batchelor, G. K, Transport properties of two-phase materials with random structure. Transport properties of two-phase materials with random structure 6, 277–255 (1974)

    MATH  Google Scholar 

  29. Batchelor, G. K, Diffusion of particles with hydrodynamic interaction. Diffusion of particles with hydrodynamic interaction 74, 1–29 (1976)

    MathSciNet  MATH  Google Scholar 

  30. Tam, C. K. W, The drag on a cloud of spherical particles in low Reynolds number flow. The drag on a cloud of spherical particles in low Reynolds number flow 38, 537–546 (1969)

    MATH  Google Scholar 

  31. Charm, S. E. and Kurland, G. S. Blood Flow and Micro-Circulation, John Wiley, New York (1974)

    Google Scholar 

  32. Waller, B. F., Orr, C. M., Slack, J. D., Pinkerton, C. A., van Tassel, J., and Peters, T, Anatomy, histology, and pathology of coronary arteries: a review relevant to new interventional and imaging techniques-part I. Anatomy, histology, and pathology of coronary arteries: a review relevant to new interventional and imaging techniques-part I 15, 451–457 (1992)

    Google Scholar 

  33. Lighthill, J. Waves in Fluids, Cambridge University Press, Cambridge (1978)

    MATH  Google Scholar 

  34. Chung, S. and Vafai, K, Mechanobiology of low-density lipoprotein transport within an arterial wall-impact of hyperthermia and coupling effects. Mechanobiology of low-density lipoprotein transport within an arterial wall-impact of hyperthermia and coupling effects 47, 137–147 (2014)

    Google Scholar 

  35. Keangin, P., Vafai, K., and Rattanadecho, P, Electromagnetic field effects on biological materials. Electromagnetic field effects on biological materials 65, 389–399 (2013)

    Google Scholar 

  36. Goodarzi, M., Safaei, M. R., Vafai, K., Ahmadi, G., Dahari, M., Kazi, S. N., and Jomhari, N, Investigation of nanofluid mixed convection in a shallow cavity using a two-phase mixture model. Investigation of nanofluid mixed convection in a shallow cavity using a two-phase mixture model 75, 204–220 (2014)

    Google Scholar 

  37. Hayat, T., Saleem, N., Abd Elmaboud, Y., Asghar, S, Peristaltic flow of a second-order fluid in the presence of an induced magnetic field. Peristaltic flow of a second-order fluid in the presence of an induced magnetic field 67, 537–558 (2011)

    MathSciNet  MATH  Google Scholar 

  38. Mekheimer, K. S. and Abd Elmaboud, Y, Peristaltic transport of a particle-fluid suspension through a uniform and non-uniform annulus. Peristaltic transport of a particle-fluid suspension through a uniform and non-uniform annulus 5, 47–57 (2008)

    MATH  Google Scholar 

  39. Kamel, M. H., Eldesoky, I. M., Maher, B. M., and Abumandour, R. M, Slip effects on peristaltic transport of a particle-fluid suspension in a planar channel. Slip effects on peristaltic transport of a particle-fluid suspension in a planar channel 2015, 1–14 (2015)

    Google Scholar 

  40. Chinjung, Y. and Eugene, C. E, Transient lateral transport of platelet-sized particles in flowing blood suspensions. Biophysical Journal 66, 1706–1716 (1994)

    Article  Google Scholar 

Download references

Acknowledgements

S. I. ABDELSALAM thanks the Binational Fulbright Commission in Egypt and the Council for International Exchange of Scholars in U. S.A. for the honor of the Fulbright Egyptian Scholar Award for the year (2015–2016). In addition, the first two authors declare that they contributed to this work equally.

Author information

Authors and Affiliations

  1. Department of Basic Engineering Sciences, Faculty of Engineering, Menoufia University, Menoufia, 32511, Egypt

    I. M. Eldesoky & R. M. Abumandour

  2. Department of Mechanical Engineering, University of California, Riverside, California, 92521, USA

    S. I. Abdelsalam & K. Vafai

  3. Basic Science Department, Faculty of Engineering, The British University in Egypt, Cairo, 11837, Egypt

    S. I. Abdelsalam

  4. Department of Engineering Mathematics and Physics, Faculty of Engineering, Cairo University, Giza, 12613, Egypt

    M. H. Kamel

Authors
  1. I. M. Eldesoky
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. I. Abdelsalam
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. R. M. Abumandour
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. H. Kamel
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. K. Vafai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. I. Abdelsalam.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Eldesoky, I.M., Abdelsalam, S.I., Abumandour, R.M. et al. Interaction between compressibility and particulate suspension on peristaltically driven flow in planar channel. Appl. Math. Mech.-Engl. Ed. 38, 137–154 (2017). https://doi.org/10.1007/s10483-017-2156-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-017-2156-6

Keywords

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation