Skip to main content
SpringerLink
Log in

Electric admittance analysis of quartz crystal resonator in thickness-shear mode induced by array of surface viscoelastic micro-beams

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

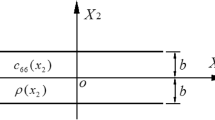
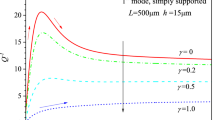
The electric admittance of a compound system composed of a thicknessshear mode (TSM) quartz crystal resonator (QCR) and an array of surface viscoelastic micro-beams (MBs) is studied. The governing equations of the MBs are derived from the Timoshenko-beam theory in consideration of shear deformation. The electrical admittance is described directly in terms of the physical properties of the surface epoxy resin (SU-8) MBs from an electrically forced vibration analysis. It is found that both the inertia effect and the constraint effect of the MBs produce competitive influence on the resonant frequency and admittance of the compound QCR system. By further comparing the numerical results calculated from the Timoshenko-beam model with those from the Euler-beam model, the shear deformation is found to lead to some deviation of an admittance spectrum. The deviations are revealed to be evident around the admittance peak(s) and reach the maximum when a natural frequency of the MBs is identical to the fundamental frequency of the QCR. Besides, a higher order vibration mode of the MBs corresponds to a larger deviation at the resonance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Benes, E, Improved quartz crystal microbalance technique. Improved quartz crystal microbalance technique 56, 608–626 (1984)

    Google Scholar 

  2. Li, F., Wang, J. H. C., and Wang, Q. M, Thickness shear mode acoustic wave sensors for characterizing the viscoelastic properties of cell monolayer. Thickness shear mode acoustic wave sensors for characterizing the viscoelastic properties of cell monolayer 128, 399–406 (2008)

    Google Scholar 

  3. Li, N., Qian, Z., and Yang, J, Effects of nonlinearity on transient processes in AT-cut quartz thickness-shear resonators. Effects of nonlinearity on transient processes in AT-cut quartz thickness-shear resonators 28, 347–352 (2015)

    Google Scholar 

  4. Reed, C. E., Kanazawa, K. K., and Kaufman, J. H, Physical description of a viscoelastically loaded AT-cut quartz resonator. Physical description of a viscoelastically loaded AT-cut quartz resonator 68, 1993–2001 (1990)

    Google Scholar 

  5. Sauerbrey, G, Verwendung von Schwingquarzen zur Wägung dunner Schichten und zur Mikrowägung. Verwendung von Schwingquarzen zur Wägung dunner Schichten und zur Mikrowägung 155, 206–222 (1959)

    Google Scholar 

  6. Liu, N., Yang, J. M., and Wang, J, Shear vibration of a crystal plate carrying an array of microbeams. Shear vibration of a crystal plate carrying an array of microbeams 91, 572–581 (2011)

    Google Scholar 

  7. Zhang, R. Y., Xie, J., Hu, Y. T., and Chen, X. D, Thickness-shear vibration of an elastic plate carrying an array of rigid microbeams with consideration of couple stresses. Thickness-shear vibration of an elastic plate carrying an array of rigid microbeams with consideration of couple stresses 51, 179–189 (2012)

    MathSciNet  Google Scholar 

  8. Kong, L. C., Xie, X., Zhang, J., Wang, Y. X., and Hu, Y. T, On the interaction between a quartz crystal resonator and an array of micro-beams in thickness-shear vibrations. On the interaction between a quartz crystal resonator and an array of micro-beams in thickness-shear vibrations 28, 464–470 (2015)

    Google Scholar 

  9. Kong, L. C., Hu, H., and Hu, Y. T, Effect of shear deformation on frequency shift of a microbeams/ resonator system under thickness-shear vibrations (in Chinese). Effect of shear deformation on frequency shift of a microbeams/ resonator system under thickness-shear vibrations (in Chinese) 33, 75–78 (2014)

    Google Scholar 

  10. Kong, L. C. and Hu, Y. T, Effect of strain-gradients of surface micro-beams on frequency-shift of a quartz crystal resonator under thickness-shear vibrations. Effect of strain-gradients of surface micro-beams on frequency-shift of a quartz crystal resonator under thickness-shear vibrations 31, 647–652 (2015)

    MathSciNet  MATH  Google Scholar 

  11. Xie, X., Kong, L. C., Wang, Y. X., Zhang, J., and Hu, Y. T, Coupled vibrations and frequency shift of compound system consisting of quartz crystal resonator in thickness-shear motions and micro-beam array immersed in liquid. Coupled vibrations and frequency shift of compound system consisting of quartz crystal resonator in thickness-shear motions and micro-beam array immersed in liquid 36(2), 225–232 (2015) DOI 10.1007/s10483-015-1902-7

    MathSciNet  Google Scholar 

  12. Geim, A. K., Dubonos, S. V., Grigorieva, I. V., Novoselov, K. S., Zhukov, A. A., and Shapoval, S. Y, Microfabricated adhesive mimicking gecko foot-hair. Microfabricated adhesive mimicking gecko foot-hair 2, 461–463 (2003)

    Google Scholar 

  13. Nomura, S., Kojima, H., Ohyabu, Y., Kuwabara, K., Miyauchi, A., and Uemura, T, Cell culture on nanopillar sheet: study of HeLa cells on nanopillar sheet. Cell culture on nanopillar sheet: study of HeLa cells on nanopillar sheet 44, L1184–L1186 (2005)

    Google Scholar 

  14. McAllister, D. V., Wang, P. M., Davis, S. P., Park, J. H., Canatella, P. J., Allen, M. G., and Prausnitz, M. R, Microfabricated needles for transdermal delivery of macromolecules and nanoparticles: fabrication methods and transport studies. Microfabricated needles for transdermal delivery of macromolecules and nanoparticles: fabrication methods and transport studies 100, 13755–13760 (2003)

    Google Scholar 

  15. Hossenlopp, J., Jiang, L., Cernosek, R., and Josse, F, Characterization of epoxy resin (SU-8) film using thickness-shear mode (TSM) resonator under various conditions. Characterization of epoxy resin (SU-8) film using thickness-shear mode (TSM) resonator under various conditions 42, 2373–2384 (2004)

    Google Scholar 

  16. Liu, J., Cai, B., Zhu, J., Ding, G., Zhao, X., Yang, C., and Chen, D, Process research of high aspect ratio microstructure using SU-8 resist. Process research of high aspect ratio microstructure using SU-8 resist 10, 265–268 (2004)

    Google Scholar 

  17. Timoshenko, S. P. LXVI, On the correction for shear of the differential equation for transverse vibrations of prismatic bars. On the correction for shear of the differential equation for transverse vibrations of prismatic bars 41, 744–746 (1921)

    Google Scholar 

  18. Tiersten, H. F. Linear Piezoelectric Plate Vibrations, Springer, Boston (1969)

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Civil Engineering and Mechanics, Huazhong University of Science and Technology, Wuhan, 430074, China

    Jiemin Xie & Yuantai Hu

Authors
  1. Jiemin Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuantai Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuantai Hu.

Additional information

Project supported by the National Natural Science Foundation of China (Nos. 11272127 and 51435006) and the Research Fund for the Doctoral Program of Higher Education of China (No. 20130142110022)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xie, J., Hu, Y. Electric admittance analysis of quartz crystal resonator in thickness-shear mode induced by array of surface viscoelastic micro-beams. Appl. Math. Mech.-Engl. Ed. 38, 29–38 (2017). https://doi.org/10.1007/s10483-017-2154-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-017-2154-6

Keywords

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation