Abstract
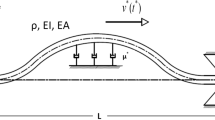
Under the 3:1 internal resonance condition, the steady-state periodic response of the forced vibration of a traveling viscoelastic beam is studied. The viscoelastic behaviors of the traveling beam are described by the standard linear solid model, and the material time derivative is adopted in the viscoelastic constitutive relation. The direct multi-scale method is used to derive the relationships between the excitation frequency and the response amplitudes. For the first time, the real modal functions are employed to analytically investigate the periodic response of the axially traveling beam. The undetermined coefficient method is used to approximately establish the real modal functions. The approximate analytical results are confirmed by the Galerkin truncation. Numerical examples are presented to highlight the effects of the viscoelastic behaviors on the steady-state periodic responses. To illustrate the effect of the internal resonance, the energy transfer between the internal resonance modes and the saturation-like phenomena in the steady-state responses is presented.
Article PDF
Similar content being viewed by others
Change history
20 February 2018
The article “<Emphasis Type="Bold">Primary resonance of traveling viscoelastic beam under internal resonance</Emphasis>”, written by Hu DING, Linglu HUANG, Xiaoye MAO, and Liqun CHEN, was originally published Online First without open access. After publication in Volume 38, Issue 1, Page 1–14, the authors decided to opt for Open Choice and to make the article an open access publication. Therefore, the copyright of the article has been changed to © The Author(s) 2018 and the article is forthwith distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The original article has been corrected.
References
Zhu, W. D., Guo, B. Z., and Mote, C. D. Stabilization of a translating tensioned beam through a pointwise control force. Journal of Dynamic Systems Measurement and Control-Transactions of the ASME, 122, 322–331 (2000)
Yang, T. Z. and Yang, X. D. Exact solution of supercritical axially moving beams: symmetric and anti-symmetric configurations. Archive of Applied Mechanics, 83, 899–906 (2013)
Sandilo, S. H. and van Horssen, W. T. On boundary damping for an axially moving tensioned beam. Journal of Vibration and Acoustics-Transactions of the ASME, 134, 011005 (2012)
Marynowski, K. and Kapitaniak, T. Dynamics of axially moving continua. International Journal of Mechanical Sciences, 81, 26–41 (2014)
Yao, M. H. and Zhang, W. Multi-pulse homoclinic orbits and chaotic dynamics in motion of parametrically excited viscoelastic moving belt. International Journal of Nonlinear Sciences and Numerical Simulation, 6, 37–45 (2005)
Ozhan, B. B. and Pakdemirli, M. A general solution procedure for the forced vibrations of a continuous system with cubic nonlinearities: primary resonance case. Journal of Sound and Vibration, 325, 894–906 (2009)
Ozhan, B. B. and Pakdemirli, M. Effect of viscoelasticity on the natural frequencies of axially moving continua. Advances in Mechanical Engineering, 5, 169598 (2013)
Yang, X. D. and Zhang, W. Nonlinear dynamics of axially moving beam with coupled longitudinal-transversal vibrations. Nonlinear Dynamics, 78, 2547–2556 (2014)
Ding, H. and Zu, J. W. Steady-state responses of pulley-belt systems with a one-way clutch and belt bending stiffness. Journal of Vibration and Acoustics-Transactions of the ASME, 136, 041006 (2014)
Yan, Q. Y., Ding, H. and Chen, L. Q. Nonlinear dynamics of axially moving viscoelastic Timoshenko beam under parametric and external excitations. Applied Mathematics and Mechanics (English Edition), 36, 971–984 (2015) DOI 10.1007/s10483-015-1966-7
Tang, Y. Q., Zhang, D. B., and Gao, J. M. Parametric and internal resonance of axially accelerating viscoelastic beams with the recognition of longitudinally varying tensions. Nonlinear Dynamics, 83, 401–418 (2016)
Wang, L. H., Hu, Z. D., Zhong, Z., and Ju, J. W. Dynamic analysis of an axially translating viscoelastic beam with an arbitrarily varying length. Acta Mechanica, 214, 225–244 (2010)
Chen, L. Q. and Chen, H. Asymptotic analysis on nonlinear vibration of axially accelerating viscoelastic strings with the standard linear solid model. Journal of Engineering Mathematics, 67, 205–218 (2010)
Wang, B. Asymptotic analysis on weakly forced vibration of axially moving viscoelastic beam constituted by standard linear solid model. Applied Mathematics and Mechanics (English Edition), 33, 817–828 (2012) DOI 10.1007/s10483-012-1588-8
Saksa, T. and Jeronen, J. Dynamic analysis for axially moving viscoelastic Poynting-Thomson beams. Mathematical Modeling and Optimization of Complex Structures, 40, 131–151 (2016)
Ghayesh, M. H. and Amabili, M. Nonlinear stability and bifurcations of an axially moving beam in thermal environment. Journal of Vibration and Control, 21, 2981–2994 (2015)
Sze, K. Y., Chen, S. H., and Huang, J. L. The incremental harmonic balance method for nonlinear vibration of axially moving beams. Journal of Sound and Vibration, 281, 611–626 (2005)
Huang, J. L., Su, R. K. L., Li, W. H., and Chen, S. H. Stability and bifurcation of an axially moving beam tuned to three-to-one internal resonances. Journal of Sound and Vibration, 330, 471–485 (2011)
Wang, L. H., Ma, J. J., Yang, M. H., Li, L. F., and Zhao, Y. Y. Multimode dynamics of inextensional beams on the elastic foundation with two-to-one internal resonances. Journal of Applied Mechanics-Transactions of the ASME, 80, 061016 (2013)
Sahoo, B., Panda, L. N., and Pohit, G. Combination, principal parametric and internal resonances of an accelerating beam under two frequency parametric excitation. International Journal of Non-Linear Mechanics, 78, 35–44 (2016)
Ding, H., Zhang, G. C., Chen, L. Q., and Yang, S. P. Forced vibrations of supercritically transporting viscoelastic beams. Journal of Vibration and Acoustics-Transactions of the ASME, 134, 051007 (2012)
Liu, D. Xu, W. and Xu, Y. Dynamic responses of axially moving viscoelastic beam under a randomly disordered periodic excitation. Journal of Sound and Vibration, 331, 4045–4056 (2012)
Ding, H. and Zu, J. W. Periodic and chaotic responses of an axially accelerating viscoelastic beam under two-frequency excitations. International Journal of Applied Mechanics, 5, 1350019 (2013)
Kang, H. J., Zhao, Y. Y., and Zhu, H. P. Out-of-plane free vibration analysis of a cable-arch structure. Journal of Sound and Vibration, 332, 907–921 (2013)
Ding, H. Steady-state responses of a belt-drive dynamical system under dual excitations ACTA Mechanics Sinica, 32, 156–169 (2016)
Zhang, J. R., Guo, Z. X., Zhang, Y., Tang, L., and Guan, X. Inner structural vibration isolation method for a single control moment gyroscope. Journal of Sound and Vibration, 361, 78–98 (2016)
Li, X. H. and Hou, J. Y. Bursting phenomenon in a piecewise mechanical system with parameter perturbation in stiffness. International Journal of Non-Linear Mechanics, 81, 165–176 (2016)
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the State Key Program of the National Natural Science Foundation of China (No. 11232009) and the National Natural Science Foundation of China (Nos. 11372171 and 11422214)
The original version of this article was revised due to a retrospective Open Access order.
A correction to this article is available at https://doi.org/10.1007/s10483-018-2269-6
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
This article is published with open access at Springerlink.com, corrected publication 03/2018
The original article has been corrected.
About this article
Cite this article
Ding, H., Huang, L., Mao, X. et al. Primary resonance of traveling viscoelastic beam under internal resonance. Appl. Math. Mech.-Engl. Ed. 38, 1–14 (2017). https://doi.org/10.1007/s10483-016-2152-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-016-2152-6