Abstract
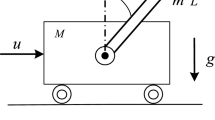
A model of two oscillating pendula placed on a mobile support is studied. Once an overall scheme of equations, under general assumptions, is formulated via the Lagrangian equations of motion, the specific case of absence of escapement is examined. The mechanical model consists of two coupled pendula both oscillating on a moving board attached to a spring. The final result performs selection among the peculiar parameters of the physical process (the length, the ratio of masses, the friction and damping coefficients, and the stiffness of the spring), providing a tendency to synchronization.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Czolczynki, K., Perlikowski, P., Stefanski, A., and Kapitaniak, T. Huygens’ odd sympathy experiment revisited. International Journal of Bifurcation and Chaos, 21, 2047–2056 (2011)
Bennett, M., Schatz, M. F., Rockwood, H., and Wiesenfeld, K. Huygens’s clocks. Proceedings of the Royal Society of London A, 458, 563–579 (2002)
Oud, W., Nijmeijer, H., and Pogromsky, A. Experimental results on Huygens synchronization. First IFAC Conference on Analysis and Control of Chaotic Systems, 39, 113–118 (2006)
Dilão, R. Anti-phase and in-phase synchronization of nonlinear oscillators: the Huygens’s clocks system. Chaos, 19, 023118 (2009)
Fradkov, A. L. and Andrievsky, B. Synchronization and phase relations in the motion of twopendulums system. International Journal of Non-Linear Mechanics, 42, 895–901 (2007)
Kumon, M., Washizaki, R., Sato, J., Kohzawa, R., Mizumoto, I., and Iwai, Z. Controlled synchronization of two 1-DOF coupled oscillators. 15th IFAC World Congress, 35, 109–114 (2002)
Gantmacher, F. R. Applications of the Theory of Matrices, Translated and Revised by J. L. Brenner, Interscience Publishers, New York (1959)
Gelfand, I. M., Kapranov, M. M., and Zelevinsky, A. V. Discriminants, Resultants and Multidimensional Determinants, Birkhäuser, Boston (1994)
Eneström, G. Remarque sur un théorème relatif aux racines delquation a n x n+a n1 x n1 +· · · a 1 x+ a 0 = 0 où tous les coefficientes a sont réels et positifs. Tôhoku Mathematical Journal, 18, 34–36 (1920)
Rather, N. A. and Gulzar, S. On the Eneström-Kakeya theorem. Acta Mathematica Universitatis Comenianae, 83, 291–302 (2014)
Kakeya, S. On the limits of the roots of an algebraic equation with positive coefficients. Tôhoku Mathematical Journal, 2, 140–142 (1912)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Talamucci, F. Synchronization of two coupled pendula in absence of escapement. Appl. Math. Mech.-Engl. Ed. 37, 1721–1738 (2016). https://doi.org/10.1007/s10483-016-2150-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-016-2150-8