Skip to main content
SpringerLink
Log in

Heat transfer characteristics of thin power-law liquid films over horizontal stretching sheet with internal heating and variable thermal coefficient

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

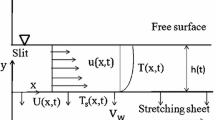
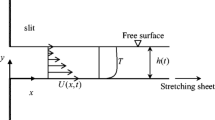
The effect of internal heating source on the film momentum and thermal transport characteristic of thin finite power-law liquids over an accelerating unsteady horizontal stretched interface is studied. Unlike most classical works in this field, a general surface temperature distribution of the liquid film and the generalized Fourier’s law for varying thermal conductivity are taken into consideration. Appropriate similarity transformations are used to convert the strongly nonlinear governing partial differential equations (PDEs) into a boundary value problem with a group of two-point ordinary differential equations (ODEs). The correspondence between the liquid film thickness and the unsteadiness parameter is derived with the BVP4C program in MATLAB. Numerical solutions to the self-similarity ODEs are obtained using the shooting technique combined with a Runge-Kutta iteration program and Newton’s scheme. The effects of the involved physical parameters on the fluid’s horizontal velocity and temperature distribution are presented and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a, b :

positive constant, s-1

C p :

specific heat capacity, J · kg-1 · K-1

d :

positive constant, m-r1

f :

dimensionless stream function

h :

liquid film thickness, m

K :

viscosity coefficient, kg · m-1 · sn-2

k :

effective thermal conductivity, W· m-1 · K-1

n :

power-law index

Pr :

generalized Prandtl number

Re x :

local Reynolds number

r 1 :

r 2, power indices

S :

unsteadiness parameter

S 0 :

critical value

T :

temperature, K

T 0 :

temperature at origin, K

T ref :

standard temperature, K

T s :

temperature of stretched surface, K

t :

time, s

u, v :

liquid velocity components along with x-direction and y-direction, respectively, m · s-1

u s :

horizontal velocity of stretched surface, m · s-1

x, y :

streamwise coordinate and cross-stream coordinate, respectively, m.

β :

dimensionless film thickness

η :

similarity variable

θ :

dimensionless temperature

ρ :

density, kg · m-3

τ xy :

modified shear viscous drag, N · m-2

φ :

heating source parameter

ψ :

stream function, m2 · s-1

ω :

consistency thermal coefficient, kg · m · sn-4 · K-1 s, for wall surface or stretched surface.

References

  1. Wang, C. Y. Liquid film on an unsteady stretching surface. Quarterly of Applied Mathematics, 48, 601–610 (1990)

    MathSciNet  MATH  Google Scholar 

  2. Andersson, H. I., Aarseth, J. B., and Dandapat, B. S. Heat transfer in a liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 43, 69–74 (2000)

    Article  MATH  Google Scholar 

  3. Liu, I. C. and Andersson, H. I. Heat transfer in a liquid film on an unsteady stretching sheet. International Journal of Thermal Sciences, 47, 766–772 (2008)

    Article  Google Scholar 

  4. Wang, C. Analytic solutions for a liquid film on an unsteady stretching surface. Heat and Mass Transfer, 42, 759–766 (2006)

    Article  Google Scholar 

  5. Rashidi, M. M. and Keimanesh, M. Using differential transform method and Padé approximant for solving MHD flow in a laminar liquid film from a horizontal stretching surface. Mathematical Problems in Engineering, 2010, 491319 (2010)

    MATH  Google Scholar 

  6. Aziz, R. C. and Hashim, I. Liquid film on unsteady stretching sheet with general surface temperature and viscous dissipation. Chinese Physics Letters, 27, 1–4 (2010)

    Article  Google Scholar 

  7. Aziz, R. C., Hashim, I., and Alomari, A. K. Thin film flow and heat transfer on an unsteady stretching sheet with internal heating. Meccanica, 46, 349–357 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  8. Dandapat, B. S., Santra, B., and Vajravelu, K. The effects of variable fluid properties and thermocapillarity on the flow of a thin film on an unsteady stretching sheet. International Journal of Heat and Mass Transfer, 50, 991–996 (2007)

    Article  MATH  Google Scholar 

  9. Noor, N. F. M. and Hashim, I. Thermocapillarity and magnetic field effects in a thin liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 53, 2044–2051 (2010)

    Article  MATH  Google Scholar 

  10. Aziz, R. C., Hashim, I., and Abbasbandy, S. Effects of thermocapillarity and thermal radiation on flow and heat transfer in a thin liquid film on an unsteady stretching sheet. Mathematical Problems in Engineering, 2012, 127320 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  11. Noor, N. F. M, Abdulaziz, O., and Hashim, I. MHD flow and heat transfer in a thin film on an unsteady stretching sheet by the homotopy analysis method. International Journal for Numerical Methods in Fluids, 63, 357–373 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Liu. I. C. and Megahed, A. M. Numerical study for the flow and heat transfer in a thin liquid film over an unsteady stretching sheet with variable fluid properties in the presence of thermal radiation. Journal of Mechanics, 28, 291–297 (2012)

    Article  Google Scholar 

  13. Liu, I. C., Wang, H. H., and Umavathi, J. C. Effect of viscous dissipation, internal heat source/sink, and thermal radiation on a hydromagnetic liquid film over an unsteady stretching sheet. Journal of Heat Transfer, 135, 031701 (2013)

    Article  Google Scholar 

  14. Nandeppanavar, M. M., Vajravelu, K., Abel, M. S., Ravi, S., and Jyoti, H. Heat transfer in a liquid film over an unsteady stretching sheet. International Journal of Heat and Mass Transfer, 55, 1316–1324 (2012)

    Article  MATH  Google Scholar 

  15. Andersson, H. I., Aarseth, J. B., Braud, N., and Dandapat, B. S. Flow of a power-law fluid film on unsteady stretching surface. Journal of Non-Newtonian Fluid Mechanics, 62, 1–8 (1996)

    Article  Google Scholar 

  16. Chen, C. Heat transfer in a power-law fluid film over an unsteady stretching sheet. Heat and Mass Transfer, 39, 791–796 (2003)

    Article  Google Scholar 

  17. Chen, C. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. Journal of Non-Newtonian Fluid Mechanics, 135, 128–135 (2006)

    Article  MATH  Google Scholar 

  18. Chen, C. Marangoni effects on forced convection of power-law liquids in a thin film over a stretching surface. Physics Letters A, 370, 51–57 (2007)

    Article  Google Scholar 

  19. Wang, C. and Pop, I. Analysis of the flow of a power-law fluid film on an unsteady stretching surface by means of homotopy analysis method. Journal of Non-Newtonian Fluid Mechanics, 138, 161–172 (2006)

    Article  MATH  Google Scholar 

  20. Abbas, Z., Hayat, T., Sajid, M., and Asghar, S. Unsteady flow of a second grade fluid film over an unsteady stretching sheet. Mathematical and Computer Modelling, 48, 518–526 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  21. Elgazery, N. S. and Hassan, M. A. The effects of variable fluid properties and magnetic field on the flow of non-Newtonian fluid film on an unsteady stretching sheet through a porous medium. Communications in Numerical Methods in Engineering, 24, 2113–2129 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  22. Mahmoud, M. A. A. and Megahed, A. M. MHD flow and heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet with variable fluid properties. Canadian Journal of Physics, 87, 1065–1071 (2009)

    Article  Google Scholar 

  23. Huang, K. H., Tsai, R., and Huang, C. H. Chebyshev finite difference approach to modeling the thermoviscosity effect in a power-law liquid film on an unsteady stretching surface. Journal of Non-Newtonian Fluid Mechanics, 165, 1351–1356 (2010)

    Article  MATH  Google Scholar 

  24. Vajravelu, K., Prasad, K. V., and Ng, C. Unsteady flow and heat transfer in a thin film of Ostwaldde Waele liquid over a stretching surface. Communications in Nonlinear Science and Numerical Simulation, 17, 4163–4173 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  25. Vajravelu, K., Prasad, K. V., and Raju, B. T. Effects of variable fluid properties on the thin film flow of Ostwald-de Waele fluid over a stretching surface. Journal of Hydrodynamics, 25, 10–19 (2013)

    Article  Google Scholar 

  26. Lin, Y. H., Zheng, L. C., and Chen, G. Unsteady flow and heat transfer of pseudo-plastic nanoliquid in a finite thin film on a stretching surface with variable thermal conductivity and viscous dissipation. Powder Technology, 274, 324–332 (2015)

    Article  Google Scholar 

  27. Lin, Y. H., Zheng, L. C., Zhang, X. X., Ma, L. X., and Chen, G. MHD pseudo-plastic nanofluid unsteady flow and heat transfer in a finite thin film over stretching surface with internal heat generation. International Journal of Heat and Mass Transfer, 84, 903–911 (2015)

    Article  Google Scholar 

  28. Pop, I., Rashidi, M., and Gorla, R. S. R. Mixed convection to power-law type non-Newtonian fluids from a vertical wall. Polymer-Plastics Technology Engineering, 30, 47–66 (1991)

    Article  Google Scholar 

  29. Gorla, R. S. R., Pop, I., and Lee, J. K. Convective wall plume in power-law fluid: second-order correction for the adiabatic wall. Wärme-und Stoffübertragung, 27, 473–479 (1992)

    Article  Google Scholar 

  30. Chamkha, A. J. Similarity solution for thermal boundary layer on a stretched surface of a nonNewtonian fluid. International Communications in Heat and Mass Transfer, 24, 643–652 (1997)

    Article  Google Scholar 

  31. Zheng, L. C., Zhang, X. X., and Ma, L. X. Fully developed convective heat transfer for power law fluids in a circular tube. Chinese Physics Letters, 25, 195–197 (2008)

    Article  Google Scholar 

  32. Zheng, L. C., Lin, Y. H., and Zhang, X. X. Marangoni convection of power law fluids driven by power-law temperature gradient. Journal of the Franklin Institute, 349, 2585–2597 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  33. Lin, Y. H., Zheng, L. C., and Zhang, X. X. Magnetohydrodynamics thermocapillary Marangoni convection heat transfer driven by temperature gradient. Journal of Heat Transfer, 135, 051702 (2013)

    Article  Google Scholar 

  34. Chen, X. H., Zheng, L. C., and Zhang, X. X. MHD of power-law fluid on moving surface with power-law velocity and special injection/blowing. Applied Mathematics and Mechanics (English Edition), 35, 1555–1564 (2014) DOI 10.1007/s10483-014-1887-6

    Article  MathSciNet  MATH  Google Scholar 

  35. Lin, Y. H., Zheng, L. C., and Zhang, X. X. Radiation effects on Marangoni convection flow and heat transfer in pseudo-plastic non-Newtonian nanofluids with variable thermal conductivity. International Journal of Heat and Mass Transfer, 77, 708–716 (2014)

    Article  Google Scholar 

  36. Lin, Y. H., Zheng, L. C., and Zhang, X. X. MHD Marangoni boundary layer flow and heat transfer of pseudo-plastic nanofluids over a porous medium with a modified model. Mechanics of Time-Dependent Materials, 19, 519–536 (2015)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, Fujian Province, China

    Yanhai Lin

  2. School of Mathematics and Physics, University of Science and Technology Beijing, Beijing, 100083, China

    Liancun Zheng

  3. Department of Physics, Blinn College, Bryan, TX, 77805, USA

    Lianxi Ma

Authors
  1. Yanhai Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Liancun Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lianxi Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yanhai Lin.

Additional information

Project supported by the Scientific Research Funds of Huaqiao University (No. 14BS310) and the National Natural Science Foundation of China (Nos. 51276014 and 51476191)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, Y., Zheng, L. & Ma, L. Heat transfer characteristics of thin power-law liquid films over horizontal stretching sheet with internal heating and variable thermal coefficient. Appl. Math. Mech.-Engl. Ed. 37, 1587–1596 (2016). https://doi.org/10.1007/s10483-016-2141-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-016-2141-8

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation