Abstract
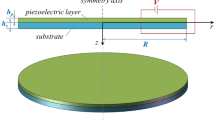
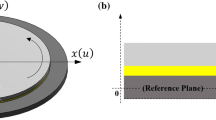
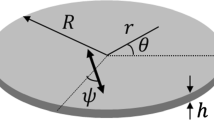
A theoretical model of a circular flexure-mode piezoelectric bimorph actuator is established. The circular bimorph structure, consisting of two flexible layers of piezoelectric material and a layer of metallic material in the middle, is powered to the flexural deformation. The analytical solutions including the statics solution and the dynamics solution are derived from the 3D equations of the linear theory of piezoelectricity. Numerical results are included to show the circular bimorph piezoelectric actuator (CBPA) performance, depending on the physical parameters.
Similar content being viewed by others
References
Schmutz, L. Adaptive optics: a modern cure for Newton tremors. Photon Spectra, 27, 119–128 (1993)
Babcock, H. W. The possibility of compensating astronomical seeing. Publications of the Astronomical Society of the Pacific, 65, 229–236 (1953)
Woolf, N. Adaptive optics. Proceedings of IAU Colloquium, Garching, Germany, 221–233 (1984)
Tyson, R. Principles of Adaptive Optics, CRC Press, Boca Raton (2010)
Hom, C. L., Dean, P. D., and Winzer, S. R. Simulating electrostrictive deformable mirrors I: nonlinear static analysis. Smart Materials and Structures, 8, 691–699 (1999)
Ning, Y. Performance Test and Application Study of a Bimorph Deformable Mirror (in Chinese), Ph.D. dissertation, National University of Defense Technology (2008)
Wilson, R., Franza, F., and Noethe, L. Active optics I: a system for optimizing the optical quality and reducing the costs of large telescopes. Journal of Modern Optics, 34, 485–509 (1987)
Hom, C. L. Simulating electrostrictive deformable mirrors II: nonlinear dynamic analysis. Smart Materials and Structures, 8, 700–708 (1999)
Lin, X. D., Xue, C., Liu, X. Y., Wang, J. L., and Wei, P. F. Current status and research development of wavefront correctors for adaptive optics. Chinese Optics, 4, 337–351 (2012)
Webber, K. G., Hopkinson, D. P., and Lynch, C. S. Application of a classical lamination theory model to the design of piezoelectric composite unimorph actuators. Journal of Intelligent Material Systems and Structures, 17, 29–34 (2006)
Hagood, N. W., Chung, W. H., and von Flotow, A. Modelling of piezoelectric actuator dynamics for active structural control. Journal of Intelligent Material Systems and Structures, 1, 327–354 (1990)
Hwang, W. S. and Park, H. C. Finite element modeling of piezoelectric sensors and actuators. AIAA Journal, 31, 930–937 (1993)
Goldfarb, M. and Celanovic, N. A lumped parameter electromechanical model for describing the nonlinear behavior of piezoelectric actuators. Journal of Dynamic Systems, Measurement, and Control, 119, 478–485 (1997)
Liu, L., Tan, K. K., Chen, S., Teo, C. S., and Lee, T. H. Discrete composite control of piezoelectric actuators for high-speed and precision scanning. IEEE Transactions on Industrial Informatics, 9, 859–868 (2013)
Vashist, S. K. and Chhabra, D. Optimal placement of piezoelectric actuators on plate structures for active vibration control using genetic algorithm. Proccedings of the SPIE, 9057, 905720 (2014)
Wang, H. R. Analytical analysis of a beam flexural-mode piezoelectric actuator for deformable mirrors. Journal of Astronomical Telescopes, Instruments, and Systems, 1, 049001 (2015)
Kamada, T., Fujita, T., Hatayama, T., Arikabe, T., Murai, N., Aizawa, S., and Tohyama, K. Active vibration control of frame structures with smart structures using piezoelectric actuators (vibration control by control of bending moments of columns). Smart Materials and Structures, 6, 448–456 (1997)
Crawley, E. F. and de Luis, J. Use of piezoelectric actuators as elements of intelligent structures. AIAA Journal, 25, 1373–1385 (1987)
Freeman, R. and Garcia, H. High-speed deformable mirror system. Applied Optics, 21, 589–595 (1982)
Wang, H. R., Hu, H. P., Yang, J. S., and Hu, Y. T. Spiral piezoelectric transducer in torsional motion as low-frequency power harvester. Applied Mathematics and Mechanics (English Edition), 34, 589–596 (2013) DOI 10.1007/s10483-013-1693-x
Wang, H. R., Xie, J. M., Xie, X., Hu, Y. T., and Wang, J. Nonlinear characteristics of circular-cylinder piezoelectric power harvester near resonance based on flow-induced flexural vibration mode. Applied Mathematics and Mechanics (English Edition), 35, 229–236 (2014) DOI 10.1007/s10483-014-1786-6
Wang, H. R., Xie, X., Hu, Y., and Wang, J. Weakly nonlinear characteristics of a three-layer circular piezoelectric plate-like power harvester near resonance. Journal of Mechanics, 30, 97–102 (2014)
Wang, H. R., Hu, Y., and Wang, J. On the nonlinear behavior of a multilayer circular piezoelectric plate-like transformer operating near resonance. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 60, 752–757 (2013)
Yang, J. An Introduction to the Theory of Piezoelectricity, Springer, New York (2005)
Wang, J., Wang, H. R., Hu, H., Luo, B., Hu, Y., and Wang, J. On the strain-gradient effects in micro piezoelectric-bimorph circular plate power harvesters. Smart Materials and Structures, 21, 015006 (2012)
Huang, Y. and Huang, W. Modeling and analysis of circular flexural-vibration-mode piezoelectric transformer. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 57, 2764–2771 (2010)
Auld, B. A. Acoustic Fields and Waves in Solids, Krieger Publishing Company, Malabar (1973)
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (Nos. 11403109, 11190014, 10921063, and 11373073) and the Natural Science Foundation of Jiangsu Province (No.BK20141042)
Rights and permissions
About this article
Cite this article
Wang, H., Hu, M. & Li, Z. Modelling and analysis of circular bimorph piezoelectric actuator for deformable mirror. Appl. Math. Mech.-Engl. Ed. 37, 639–646 (2016). https://doi.org/10.1007/s10483-016-2077-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-016-2077-8