Skip to main content
SpringerLink
Log in

Nonlinear beam formulation incorporating surface energy and size effect: application in nano-bridges

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

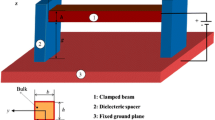
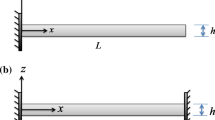
A nonlinear beam formulation is presented based on the Gurtin-Murdoch surface elasticity and the modified couple stress theory. The developed model theoretically takes into account coupled effects of the energy of surface layer and microstructures sizedependency. The mid-plane stretching of a beam is incorporated using von-Karman nonlinear strains. Hamilton’s principle is used to determine the nonlinear governing equation of motion and the corresponding boundary conditions. As a case study, pull-in instability of an electromechanical nano-bridge structure is studied using the proposed formulation. The nonlinear governing equation is solved by the analytical reduced order method (ROM) as well as the numerical solution. Effects of various parameters including surface layer, size dependency, dispersion forces, and structural damping on the pullin parameters of the nano-bridges are discussed. Comparison of the results with the literature reveals capability of the present model in demonstrating the impact of nanoscale phenomena on the pull-in threshold of the nano-bridges.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ke, C. H. and Espinosa, H. D. Nanoelectromechanical Systems (NEMS) and Modeling. Handbook of Theoretical and Computational Nanotechnology (eds. Rieth, M. and Schommers, W.), American Scientific Publishers, California, 1–38 (2006)

    Google Scholar 

  2. Zhang, L., Golod, S. V., Deckardt, E., Prinz, V., and Grützmacher, D. Free-standing Si/SiGe micro- and nano-objects. Physica E, 23(3), 280–284 (2004)

    Article  Google Scholar 

  3. Georgantzinos, S. K. and Anifantis, N. K. Carbon nanotube-based resonant nanomechanical sensors: a computational investigation of their behavior. Physica E, 42(5), 1795–1801 (2010)

    Article  Google Scholar 

  4. Gurtin, M. E. and Murdoch, A. I. A continuum theory of elastic material surfaces. Archive for Rational Mechanics and Analysis, 57(4), 291–323 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  5. Gurtin, M. E. and Murdoch, A. I. Surface stress in solids. International Journal of Solids and Structures, 14(6), 431–440 (1978)

    Article  MATH  Google Scholar 

  6. Wang, G. F. and Feng, X. Q. Surface effects on buckling of nanowires under uniaxial compression. Applied Physics Letters, 94(14), 141913 (2009)

    Article  Google Scholar 

  7. He, J. and Lilley, C. M. Surface effect on the elastic behavior of static bending nanowires. Nano Letters, 8(7), 1798–1802 (2008)

    Article  Google Scholar 

  8. Yan, Z. and Jiang, L. Y. The vibrational and buckling behaviors of piezoelectric nanobeams with surface effects. Nanotechnology, 22(24), 245703 (2011)

    Article  Google Scholar 

  9. Fu, Y. and Zhang, J. Size-dependent pull-in phenomena in electrically actuated nanobeams incorporating surface energies. Applied Mathematical Modelling, 35(2), 941–951 (2011)

    Article  MathSciNet  Google Scholar 

  10. Ma, J. B., Jiang, L., and Asokanthan, S. F. Influence of surface effects on the pull-in instability of NEMS electrostatic switches. Nanotechnology, 21(50), 505708 (2010)

    Article  Google Scholar 

  11. Koochi, A., Hosseini-Toudeshky, H., Ovesy, H. R., and Abadyan, M. Modeling the influence of surface effect on instability of nano-cantilever in presence of van der Waals force. International Journal of Structural Stability and Dynamics, 13(4), 1250072 (2013)

    Article  Google Scholar 

  12. Koochi, A., Kazemi, A., Khandani, F., and Abadyan, M. Influence of surface effects on sizedependent instability of nano-actuators in the presence of quantum vacuum fluctuations. Physica Scripta, 85(3), 035804 (2012)

    Article  MATH  Google Scholar 

  13. Rokni, H. and Lu, W. A continuum model for the static pull-in behavior of graphene nanoribbon electrostatic actuators with interlayer shear and surface energy effects. Journal of Applied Physics, 113(15), 153512 (2013)

    Article  Google Scholar 

  14. Ansari, R. and Sahmani, S. Surface stress effects on the free vibration behavior of nanoplates. International Journal of Engineering Science, 49(11), 1204–1215 (2011)

    Article  MathSciNet  Google Scholar 

  15. Fleck, N. A., Muller, G. M., Ashby, M. F., and Hutchinson, J. W. Strain gradient plasticity: theory and experiment. Acta Metallurgica et Materialia, 42(2), 475–487 (1994)

    Article  Google Scholar 

  16. Lam, D. C. C., Yang, F., Chong, A. C. M., Wang, J., and Tong, P. Experiments and theory in strain gradient elasticity. Journal of the Mechanics and Physics of Solids, 51(8), 1477–1508 (2003)

    Article  MATH  Google Scholar 

  17. McFarland, A. W. and Colton, J. S. Role of material microstructure in plate stiffness with relevance to microcantilever sensors. Journal of Micromechanics and Microengineering, 15, 1060–1067 (2005)

    Article  Google Scholar 

  18. Chong, A. C. M. and Lam, D. C. C. Strain gradient plasticity effect in indentation hardness of polymers. Journal of Materials Research, 14(10), 4103–4110 (1999)

    Article  Google Scholar 

  19. McElhaney, K. W., Valssak, J. J., and Nix, W. D. Determination of indenter tip geometry and indentation contact area for depth-sensing indentation experiments. Journal of Materials Research, 13, 1300–1306 (1998)

    Article  Google Scholar 

  20. Nix, W. D. and Gao, H. Indentation size effects in crystalline materials: a law for strain gradient plasticity. Journal of the Mechanics and Physics of Solids, 46, 411–425 (1998)

    Article  MATH  Google Scholar 

  21. Cao, Y., Nankivil, D. D., Allameh, S., an. Soboyejo W. O. Mechanical properties of Au films on silicon substrates. Materials and Manufacturing Processes, 22, 187–194 (2007)

    Google Scholar 

  22. Al-Rub, R. K. A. and Voyiadjis, G. Z. Determination of the material intrinsic length scale of gradient plasticity theory. International Journal for Multiscale Computational Engineering, 2(3), 377–400 (2004)

    Article  Google Scholar 

  23. Wang, W., Huang, Y., Hsia, K. J., Hu, K. X., and Chandra, A. A study of microbend test by strain gradient plasticity. International Journal of Plasticity, 19, 365–382 (2003)

    Article  MATH  Google Scholar 

  24. Maranganti, R. and Sharma, P. A novel atomistic approach to determine strain-gradient elasticity constants: tabulation and comparison for various metals, semiconductors, silica, polymers and the (Ir) relevance for nanotechnologies. Journal of the Mechanics and Physics of Solids, 55(9), 1823–1852 (2007)

    Article  MATH  Google Scholar 

  25. Aydogdu, M. A general nonlocal beam theory: its application to nanobeam bending, buckling and vibration. Physica E, 41(9), 1651–1655 (2009)

    Article  Google Scholar 

  26. Yang, J., Ke, L. L., and Kitipornchai, S. Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory. Physica E, 42(5), 1727–1735 (2010)

    Article  Google Scholar 

  27. Ejike, U. B. The plane circular crack problem in the linearized couple-stress theory. International Journal of Engineering Science, 7(9), 947–961 (1969)

    Article  MATH  Google Scholar 

  28. Kishida, M., Sasaki, K., and Ishii, S. Torsion of a circular bar with annular groove in couple-stress theory. International Journal of Engineering Science, 28(8), 773–781 (1990)

    Article  Google Scholar 

  29. Yang, F. A. C. M., Chong, A. C. M., Lam, D. C. C., and Tong, P. Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures, 39(10), 2731–2743 (2002)

    Article  MATH  Google Scholar 

  30. Cosserat, E. and Cosserat, F. Theorie des Corps Deformables, Hermann et Fils, Paris (1909)

    MATH  Google Scholar 

  31. Toupin, R. A. Elastic materials with couple stresses. Archive for Rational Mechanics and Analysis, 11, 385–414 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  32. Koiter, W. T. Couple-stresses in the theory of elasticity: I and II. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen: Series B, 67(1), 17–44 (1964)

    MathSciNet  MATH  Google Scholar 

  33. Mindlin, R. D. Micro-structure in linear elasticity. Archive for Rational Mechanics and Analysis, 16, 51–78 (1964)

    Article  MathSciNet  MATH  Google Scholar 

  34. Mindlin, R. D. and Eshel, N. N. On first strain-gradient theories in linear elasticity. International Journal of Solids and Structures, 4, 109–124 (1968)

    Article  MATH  Google Scholar 

  35. Park, S. K. and Gao, X. L. Bernoulli-Euler beam model based on a modified couple stress theory. Journal of Micromechanics and Microengineering, 16(11), 2355 (2006)

    Article  Google Scholar 

  36. Beni, Y. T., Koochi, A., and Abadyan, M. Theoretical study of the effect of Casimir force, elastic boundary conditions and size dependency on the pull-in instability of beam-type NEMS. Physica E, 43(4), 979–988 (2011)

    Article  Google Scholar 

  37. Ma, H. M., Gao, X. L., and Reddy, J. N. A microstructure-dependen. Timoshenko beam model based on a modified couple stress theory. Journal of the Mechanics and Physics of Solids, 56(12), 3379–3391 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  38. Ke, L. L., Wang, Y. S., Yang, J., and Kitipornchai, S. Nonlinear free vibration of size-dependent functionally graded microbeams. International Journal of Engineering Science, 50(1), 256–267 (2012)

    Article  MathSciNet  Google Scholar 

  39. Asghari, M., Ahmadian, M. T., Kahrobaiyan, M. H., and Rahaeifard, M. On the size-dependent behavior of functionally graded micro-beams. Materials and Design, 31(5), 2324–2329 (2010)

    Article  Google Scholar 

  40. Abdi, J., Koochi, A., Kazemi, A. S., and Abadyan, M. Modeling the effects of size dependence and dispersion forces on the pull-in instability of electrostatic cantilever NEMS using modified couple stress theory. Smart Materials and Structures, 20(5), 055011 (2011)

    Article  Google Scholar 

  41. Baghani, M. Analytical study on size-dependent static pull-in voltage of microcantilevers using the modified couple stress theory. International Journal of Engineering Science, 54, 99–105 (2012)

    Article  MathSciNet  Google Scholar 

  42. Zhang, J. and Fu, Y. Pull-in analysis of electrically actuated viscoelastic microbeams based on a modified couple stress theory. Meccanica, 47(7), 1649–1658 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  43. Ahangar, S., Rezazadeh, G., Shabani, R., Ahmadi, G., and Toloei, A. On the stability of a microbeam conveying fluid considering modified couple stress theory. International Journal of Mechanics and Materials in Design, 7(4), 327–342 (2011)

    Article  Google Scholar 

  44. Abbasnejad, B., Rezazadeh, G., and Shabani, R. Stability analysis of a capacitive FGM microbeam using modified couple stress theory. Acta Mechanica Solida Sinica, 26(4), 427–440 (2013)

    Article  Google Scholar 

  45. Gao, X. L. and Mahmoud, F. F. A new Bernoulli-Euler beam model incorporating microstructure and surface energy effects. Zeitschrift für angewandte Mathematik und Physik, 65, 393–404 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  46. Gao, X. L. and Zhang, G. Y. A microstructure- and surface energy-dependent third-order shear deformation beam model. Zeitschrift für angewandte Mathematik und Physik, 66, 1–24 (2014)

    Google Scholar 

  47. Gao, X. L. A ne. Timoshenko beam model incorporating microstructure and surface energy effects. Acta Mechanica, 226, 457–474 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  48. Wang, K. F. and Wang, B. L. Influence of surface energy on the non-linear pull-in instability of nano-switches. International Journal of Non-Linear Mechanics, 59, 69–75 (2014)

    Article  Google Scholar 

  49. Zhou, S., and Gao, X. L. Solutions of half-space and half-plane contact problems based on surface elasticity. Zeitschrift für Angewandte Mathematik und Physik, 64(1), 145–166 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  50. Lu, P., He, L. H., Lee, H. P., and Lu, C. Thin plate theory including surface effects. International Journal of Solids and Structures, 43(16), 4631–4647 (2006)

    Article  MATH  Google Scholar 

  51. Dym, C. L. and Shames, I. H. Solid Mechanics: A Variational Approach, Railway Publishing House, Beijing (1984)

    MATH  Google Scholar 

  52. Muñoz-Gamarra, J. L., Alcaine, P., Marigó, E., Giner, J., Uranga, A., Esteve, J., and Barniol, N. Integration of NEMS resonators in a 65 nm CMOS technology. Microelectronic Engineering, 110, 246–249 (2013)

    Article  Google Scholar 

  53. Dragoman, M., Dragoman, D., Coccetti, F., Plana, R., and Muller, A. A. Microwave switches based on graphene. Journal of Applied Physics, 105(5), 054309 (2009)

    Article  Google Scholar 

  54. Uranga, A., Verd, J., Marigó, E., Giner, J., Muñoz-Gamarra, J. L., and Barniol, N. Exploitation of non-linearities in CMOS-NEMS electrostatic resonators for mechanical memories. Sensors and Actuators A: Physical, 197, 88–95 (2013)

    Article  Google Scholar 

  55. Hierold, C., Jungen, A., Stampfer, C., and Helbling, T. Nano electromechanical sensors based on carbon nanotubes. Sensors and Actuators A: Physical, 136(1), 51–61 (2007)

    Article  Google Scholar 

  56. Batra, R. C., Porfiri, M., and Spinello, D. Electromechanical model of electrically actuated narrow microbeams. Journal of Microelectromechanical Systems, 15(5), 1175–1189 (2006)

    Article  Google Scholar 

  57. Klimchitskaya, G. L., Mohideen, U., and Mostepanenko, V. M. Casimir and van der Waals forces between two plates or a sphere (lens) above a plate made of real metals. Physical Review A, 61(6), 062107 (2000)

    Article  Google Scholar 

  58. Boström, M. and Sernelius, B. E. Fractional van der Waals interaction between thin metallic films. Physical Review B, 61(3), 2204–2210 (2000)

    Article  Google Scholar 

  59. Israelachvili, J. N. and Tabor, D. R. F. S. The measurement of van der Waals dispersion forces in the range 1.5 to 130 nm. Proceedings of the Royal Society of London A: Mathematical and Physical Sciences, 331(1584), 19–38 (1972)

    Article  Google Scholar 

  60. Nayfeh, A. H. Nonlinear Oscillations, John Wiley, New York (1979)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Aerospace Engineering, Amirkabir University of Technology, Tehran, 15875-4413, Iran

    A. Koochi & H. Hosseini-Toudeshky

  2. Mechanical Engineering Group, Shahrekord Branch, Islamic Azad University, Shahrekord, 8813733395, Iran

    M. Abadyan

Authors
  1. A. Koochi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. Hosseini-Toudeshky
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Abadyan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. Hosseini-Toudeshky.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Koochi, A., Hosseini-Toudeshky, H. & Abadyan, M. Nonlinear beam formulation incorporating surface energy and size effect: application in nano-bridges. Appl. Math. Mech.-Engl. Ed. 37, 583–600 (2016). https://doi.org/10.1007/s10483-016-2073-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-016-2073-8

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation