Skip to main content
SpringerLink
Log in

Mixed convection boundary layer flow past vertical flat plate in nanofluid: case of prescribed wall heat flux

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

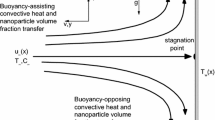
An analysis is carried out to investigate the steady mixed convection boundary layer flow of a water based nanofluid past a vertical semi-infinite flat plate. Using an appropriate similarity transformation, the governing partial differential equations are transformed into the coupled, nonlinear ordinary (similar) differential equations, which are then solved numerically for the Prandtl number P r = 6.2. The skin friction coefficient, the local Nusselt number, and the velocity and temperature profiles are presented graphically and discussed. Effects of the solid volume fraction ϕ and the mixed convection parameter λ on the fluid flow and heat transfer characteristics are thoroughly examined. Different from an assisting flow, it is found that the solutions for an opposing flow are non-unique. In order to establish which solution branch is stable and physically realizable in practice, a stability analysis is performed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Gebhart, B., Jaluria, Y., Mahajan, R. L., and Sammakia, B. Buoyancy-Induced Flows and Transport, Hemisphere, New York (1988)

    MATH  Google Scholar 

  2. Schlichting, H. and Gersten, K. Boundary Layer Theory, Springer, New York (2003)

    Google Scholar 

  3. Pop, I. and Ingham, D. B. Convective Heat Transfer: Mathematical and Computational Viscous Fluids and Porous Media, Pergamon, Oxford (2001)

    Google Scholar 

  4. Bejan, A. Convection Heat Transfer, Wiley, New Jersey (2013)

    Book  Google Scholar 

  5. Wilks, G. The flow of a uniform stream over a semi-infinite vertical flat plate with uniform surface heat flux. International Journal of Heat and Mass Transfer, 17, 743–753 (1974)

    Article  MATH  Google Scholar 

  6. Merkin, J. H. Free convection on a heated vertical plate: the solution for small Prandtl number. Journal of Engineering Mathematics, 23, 273–282 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  7. Merkin, J. H. and Mahmood, T. On the free convection boundary layer on a vertical plate with prescribed surface heat flux. Journal of Engineering Mathematics, 24, 95–107 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  8. Merkin, J. H. and Mahmood, T. Mixed convection boundary layer similarity solutions: prescribed wall heat flux. Journal of Applied Mathematics and Physics (ZAMP), 40, 51–68 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ghosh, M. S. and Yao, L. S. Mixed convection along a semi-infinite vertical flat plate with uniform surface heat flux. ASME Journal of Heat Transfer, 131, 022502-1-022502-8 (2009)

  10. Choi, S. U. S. Enhancing thermal conductivity of fluids with nanoparticles. ASME Fluids Engineering Division, 231, 99–105 (1995)

    Google Scholar 

  11. Khanafer, K., Vafai, K., and Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. International Journal of Heat and Mass Transfer, 46, 3639–3653 (2003)

    Article  MATH  Google Scholar 

  12. Ding, Y., Chen, H., Wang, L., Yang, C. Y., He, Y., Yang, W., Lee, W. P., Zhang, L., and Huo, R. Heat transfer intensification using nanofluids. Kona, 25, 23–38 (2007)

    Article  Google Scholar 

  13. Tiwari, R. K. and Das, M. K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. International Journal of Heat and Mass Transfer, 50, 2002–2018 (2007)

    Article  MATH  Google Scholar 

  14. Oztop, H. F. and Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. International Journal of Heat and Fluid Flow, 29, 1326–1336 (2008)

    Article  Google Scholar 

  15. Khanafer, K. and Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. International Journal of Heat and Mass Transfer, 54, 4410–4428 (2011)

    Article  MATH  Google Scholar 

  16. Ahmad, S. and Pop, I. Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids. International Communications in Heat and Mass Transfer, 37, 987–991 (2010)

    Article  Google Scholar 

  17. Ahmad, S., Rohni, A. M., and Pop, I. Blasius and Sakiadis problems in nanofluids. Acta Mechanica, 218, 195–204 (2011)

    Article  MATH  Google Scholar 

  18. Rohni, A. M., Ahmad, S., and Pop, I. Boundary layer flow over a moving surface in a nanofluid beneath a uniform free stream. International Journal of Numerical Methods for Heat & Fluid Flow, 21, 828–846 (2011)

    Article  Google Scholar 

  19. Rohni, A. M., Ahmad, S., and Pop, I. Flow and heat transfer over an unsteady shrinking sheet with suction in nanofluids. International Journal of Heat and Mass Transfer, 55, 1888–1895 (2012)

    Article  Google Scholar 

  20. Rohni, A. M., Ahmad, S., Merkin, J. H., and Pop, I. Mixed convection boundary layer flow along a vertical cylinder embedded in a porous medium filled by a nanofluid. Transport Porous Media, 96, 237–253 (2013)

    Article  Google Scholar 

  21. Jashim, U. M., Pop, I., and Ismail, M. A. I. Free convection boundary layer flow of a nanofluid from a convectively heated vertical plate with linear momentum slip boundary condition. Sains Malaysiana, 41, 1475–1482 (2012)

    MATH  Google Scholar 

  22. Rosca, A. V., Rosca, N. C., Grosan, T., and Pop, I. Non-Darcy mixed convection from a horizontal plate embedded in a nanofluid saturated porous media. International Communications in Heat and Mass Transfer, 39, 1080–1085 (2012)

    Article  Google Scholar 

  23. Natalia, C., Rosca, T. G. and Pop, I. Stagnation-point flow and mass transfer with chemical reaction past a permeable stretching/shrinking sheet in a nanofluid. Sains Malaysiana, 41, 1271–1279 (2012)

    Google Scholar 

  24. Bachok, N., Ishak, A., Nazar, R., and Pop, I. Flow and heat transfer at a general three-dimensional stagnation point in a nanofluid. Physica B, 405, 4914–4918 (2010)

    Article  Google Scholar 

  25. Bachok, N., Ishak, A., and Pop, I. Flow and heat transfer characteristics on a moving plate in a nanofluid. International Journal of Heat and Mass Transfer, 55, 642–648 (2012)

    Article  MATH  Google Scholar 

  26. Trimbitas, R., Grosan, T., and Pop, I. Mixed convection boundary layer flow along vertical thin needles in nanofluids. International Journal of Numerical Methods for Heat & Fluid Flow, 24, 579–594 (2014)

    Article  MathSciNet  Google Scholar 

  27. Patrulescu, F. O., Grosan, T., and Pop, I. Mixed convection boundary layer flow from a vertical truncated cone in a nanofluid. International Journal of Numerical Methods for Heat & Fluid Flow, 24, 1175–1190 (2014)

    Article  MathSciNet  Google Scholar 

  28. Das, S. K., Choi, S. U. S., Yu, W., and Pradet, T. Nanofluids: Science and Technology, Wiley, New Jersey (2007)

    Book  Google Scholar 

  29. Kakaç, S. and Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. International Journal of Heat and Mass Transfer, 52, 3187–3196 (2009)

    Article  MATH  Google Scholar 

  30. Wong, K. F. V. and Leon, O. D. Applications of nanofluids: current and future. Advances in Mechanical Engineering, 519659 (2010)

    Google Scholar 

  31. Saidur, R., Kazi, S. N., Hossain, M. S., Rahman, M. M., and Mohammed, H. A. A review on the performance of nanoparticles suspended with refrigerants and lubricating oils in refrigeration systems. Renewable and Sustainable Energy Reviews, 15, 310–323 (2011)

    Article  Google Scholar 

  32. Mahian, O., Kianifar, A., Kalogirou, S. A., Pop, I., and Wongwises, S. A review of the applications of nanofluids in solar energy. International Journal of Heat and Mass Transfer, 57, 582–594 (2013)

    Article  Google Scholar 

  33. Brinkman, H. C. The viscosity of concentrated suspensions and solutions. Journal of Chemical Physics, 20, 571–581 (1952)

    Article  Google Scholar 

  34. Weidman, P. D., Kubitschek, D. G., and Davis, A. M. J. The effect of transpiration on selfsimilar boundary layer flow over moving surface. International Journal of Engineering Science, 44, 730–737 (2006)

    Article  MATH  Google Scholar 

  35. Rosca, A. V. and Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. International Journal of Heat and Mass Transfer, 60, 355–364 (2013)

    Article  Google Scholar 

  36. Shampine, L. F., Gladwell, I., and Thompson, S. Solving ODEs with MATLAB, Cambridge University Press, Cambridge (2003)

    Book  Google Scholar 

  37. Shampine, L. F., Reichelt, M. W., and Kierzenka, J. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. http://www.mathworks.com/bvp tutorial

  38. Driscoll, T. A., Hale, N., and Trefethen, L. N. Chebfun Guide, Pafnuty Publications, Oxford (2014)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Babeş-Bolyai University, Cluj-Napoca, 400084, Romania

    R. Trîmbiƫaş, T. Grosan & I. Pop

Authors
  1. R. Trîmbiƫaş
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Grosan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. I. Pop
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. Pop.

Additional information

Project supported by the grant of the Romanian National Authority for Scientific Research, CNCSUEFISCDI (No.PN-II-RU-TE-2011-3-0013)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Trîmbiƫaş, R., Grosan, T. & Pop, I. Mixed convection boundary layer flow past vertical flat plate in nanofluid: case of prescribed wall heat flux. Appl. Math. Mech.-Engl. Ed. 36, 1091–1104 (2015). https://doi.org/10.1007/s10483-015-1967-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-015-1967-7

Keywords

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation