Skip to main content
SpringerLink
Log in

Comparison about parametric effects on wave propagation characteristics

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

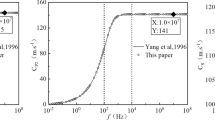
Abstract

The frequency effects on the velocities and attenuations of the bulk waves in a saturated porous medium are numerically studied in the cases of considering and neglecting the compressibility of solid grain, respectively. The results show that the whole frequency can be divided into three parts, i.e., low frequency band, medium frequency band, and high frequency band, according to the variation curves and the characteristic frequency. The compressibility of the solid grain affects the P 1 wave distinctively, the S wave tiny, and the P 2 wave little. The effects of the porosity and Poisson’s ratio on the bulk waves are numerically analyzed. It is found that both the porosity and Poisson’s ratio have obvious effects on the bulk waves. Compared with the results in the case of neglecting the porosity-moduli relation, the results in the case of considering the porosity-moduli relation are more reasonable. The results in the case of considering the porosity-moduli relation can be degenerated into the results of elastic solid and pure fluid, while the results in the case of neglecting the porosity-moduli relation cannot be degenerated into the results of elastic solid and pure fluid. Therefore, the porosity-moduli relation must be considered in the parametric study for a certain porous medium.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Yi, T. H., Li, H. N., and Gu, M. Effect of different construction materials on propagation of GPS monitoring signals. Measurement, 45, 1126–1139 (2012)

    Article  Google Scholar 

  2. Yi, T. H., Li, H. N., and Zhao, X. Y. Noise smoothing for structural vibration test signals using an improved wavelet thresholding technique. Sensors, 12, 11205–11220 (2012)

    Article  Google Scholar 

  3. De Boer, R. and Liu, Z. F. Propagation of acceleration waves in incompressible saturated porous solids. Transport in Porous Media, 21, 163–173 (1995)

    Article  Google Scholar 

  4. Yang, J. A note on Rayleigh wave velocity in saturated soils with compressible constituents. Canadian Geotechnical Journal, 38, 1360–1365 (2001)

    Article  Google Scholar 

  5. Kumar, R. and Hundal, B. S. Symmetric wave propagation in a fluid-saturated incompressible porous medium. Journal of Sound and Vibration, 288, 363–373 (2005)

    Article  Google Scholar 

  6. Kumar, R. and Hundal, B. S. Surface wave propagation in a fluid-saturated incompressible porous medium. Sadhana, 32, 155–166 (2007)

    Article  MATH  Google Scholar 

  7. Zhou, F. X., Lai, Y. M., and Song, R. X. Propagation of plane wave in non-homogeneously saturated soils. Science China Technological Sciences, 56, 430–440 (2013)

    Article  Google Scholar 

  8. Liu, Z. F. and de Boer, R. Dispersion and attenuation of surface waves in a fluid-saturated porous medium. Transport in Porous Media, 29, 207–223 (1997)

    Article  Google Scholar 

  9. Berryman, J. G. and Wang, H. F. Elastic wave propagation and attenuation in a double porosity dual-permeability medium. International Journal of Rock Mechanics and Mining Sciences, 37, 63–78 (2000)

    Article  Google Scholar 

  10. Dai, Z. J., Kuang, Z. B., and Zhao, S. X. Rayleigh waves in a double porosity half-space. Journal of Sound and Vibration, 298, 319–332 (2006)

    Article  Google Scholar 

  11. Lu, J. F., Hanyga, A., and Jeng, D. S. A linear dynamic model for a saturated porous medium. Transport in Porous Media, 68, 321–340 (2007)

    Article  MathSciNet  Google Scholar 

  12. Nenadic, I. Z., Urban, M. W., Bernal, M., and Greenleaf, J. F. Phase velocities and attenuations of shear, Lamb, and Rayleigh waves in plate-like tissues submerged in a fluid (L). Journal of the Acoustical Society of America, 130, 3549–3552 (2011)

    Article  Google Scholar 

  13. Beskos, D. E., Vgenopoulou, I., and Providakis, C. P. Dynamics of saturated rocks, II: body waves. Journal of Engineering Mechanics, 115, 996–1016 (1989)

    Article  Google Scholar 

  14. Kim, S. H., Kim, K. J., and Blouin, S. E. Analysis of wave propagation in saturated porous media, II: parametric studies. Computer Methods in Applied Mechanics and Engineering, 191, 4075–4091 (2002)

    Article  MATH  Google Scholar 

  15. Sharma, M. D. Wave propagation in a dissipative poroelastic medium. IMA Journal of Applied Mathematics, 78, 59–69 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  16. Zhang, Y., Xu, Y. X., and Xia, J. H. Analysis of dispersion and attenuation of surface waves in poroelastic media in the exploration-seismic frequency band. Geophysical Journal International, 187, 871–888 (2011)

    Article  Google Scholar 

  17. Chen, W. Y., Xia, T. D., and Hu, W. T. A mixture theory analysis for the surface wave propagation in an unsaturated porous medium. International Journal of Solids and Structures, 48, 2402–2412 (2011)

    Article  Google Scholar 

  18. Yang, J., Wu, S. M., and Cai, Y. Q. Characteristics of propagation of elastic waves in saturated soils (in Chinese). Journal of Vibration Engineering, 9, 128–137 (1996)

    Google Scholar 

  19. Biot, M. A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Journal of the Acoustical Society of America, 28, 168–191 (1956)

    Article  MathSciNet  Google Scholar 

  20. Depollier, C., Allard, J. F., and Lauriks, W. Biot theory and stress-strain equations in porous sound-absorbing materials. Journal of the Acoustical Society of America, 84, 2277–2279 (1988)

    Article  Google Scholar 

  21. Smeulders, D. M. J., de la Rosette, J. P. M., and van Dongen, M. E. H. Waves in partially saturated porous media. Transport in Porous Media, 9, 25–37 (1992)

    Article  Google Scholar 

  22. Lin, C. H., Lee, V. W., and Trifunac, M. D. The reflection of plane waves in a poroelastic half-space saturated with inviscid fluid. Soil Dynamics and Earthquake Engineering, 25, 205–223 (2005)

    Article  Google Scholar 

  23. Luo, J. and Stevens, R. Porosity-dependence of elastic moduli and hardness of 3Y-TZP ceramics. Ceramics International, 25, 281–286 (1999)

    Article  Google Scholar 

  24. Tajuddin, M. Rayleigh waves in a poroelastic half-space. Journal of the Acoustical Society of America, 75, 682–684 (1984)

    Article  MATH  Google Scholar 

  25. Yang, J. Rayleigh surface waves in an idealised partially saturated. Géotechnique, 55, 409–414 (2005)

    Article  Google Scholar 

  26. Zhang, Y., Xu, Y. X., Xia, J. H., Zhang, S. X., and Ping, P. On effective characteristic of Rayleigh surface wave propagation. Soil Dynamics and Earthquake Engineering, 57, 94–103 (2014)

    Article  Google Scholar 

  27. Singh, B. Reflection of plane waves from a free surface of a porothermoelastic solid half-space. Journal of Porous Media, 16, 945–957 (2013)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Research Center of Costal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou, 310027, China

    Zhijun Liu, Tangdai Xia & Qingqing Zheng

  2. Institute of Geotechnical Engineering, Nanjing Tech University, Nanjing, 210009, China

    Weiyun Chen

Authors
  1. Zhijun Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tangdai Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qingqing Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Weiyun Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tangdai Xia.

Additional information

Project supported by the National Natural Science Foundation of China (Nos.U1234204 and 51378463)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Z., Xia, T., Zheng, Q. et al. Comparison about parametric effects on wave propagation characteristics. Appl. Math. Mech.-Engl. Ed. 36, 763–776 (2015). https://doi.org/10.1007/s10483-015-1944-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-015-1944-6

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation