Abstract
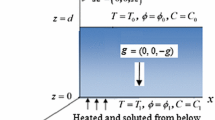
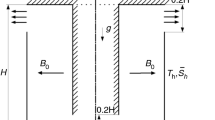
The present paper investigates the effects of a vertical magnetic field on the double diffusive nanofluid convection. The effects of the Brownian motion and thermophoresis due to the presence of nanoparticles and the effects of the Dufour and Soret parameters due to the presence of solute are included in the investigated model. The normal mode technique is used to solve the conservation equations. For the analytical study, valid approximations are made in the complex expression for the Rayleigh number to get useful and interesting results. The bottom heavy binary nanofluids are more stable than the regular binary fluids, while the top heavy binary nanofluids are less stable than the regular binary fluids. The critical wave number and the critical Rayleigh number increase whereas the frequency of oscillation (for the bottom heavy configuration) decreases when the Chandrasekhar number increases. The numerical results for the alumina-water nanofluid are studied by use of the MATHEMATICA software.
Similar content being viewed by others
References
Siginer, D. A. and Wang, H. P. Development and Applications of Non-Newtonian Flows, American Society of Mechanical Engineers, New York (1995)
Masuda, H., Ebata, A., Teramae, K., and Hishinuma, N. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra fine particles. Netsu Bussei, 7, 227–233 (1993)
Eastman, J. A., Choi, S. U. S., Yu, W., and Thompson, L. J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Applied Physics Letters, 78, 718–720 (2001)
Das, S. K. and Choi, S. U. S. A review of heat transfer in nanofluids. Advances in Heat Transfer, 41, 81–197 (2009)
Buongiorno, J. Convective transport in nanofluids. Journal of Heat Transfer, 128, 240–250 (2006)
Tzou, D. Y. Thermal instability of nanofluids in natural convection. International Journal of Heat and Mass Transfer, 51, 2967–2979 (2008)
Kuznetsov, A. V. and Nield, D. A. Thermal instability in a porous medium layer saturated by a nanofluid: Brinkman model. Transport in Porous Media, 81, 409–422 (2010)
Bhadauria, B. S. and Agarwal, S. Natural convection in a nanofluid saturated rotating porous layer: a nonlinear study. Transport in Porous Media, 87, 585–602 (2011)
Kim, J., Kang, Y. T., and Choi, C. K. Soret and Dufour effects on convective instabilities in binary nanofluids for absorption application. International Journal of Refrigeration, 30, 323–328 (2007)
Kuznetsov, A. V. and Nield, D. A. The onset of double-diffusive nanofluid convection in a layer of a saturated porous medium. Transport in Porous Media, 85, 941–951 (2010)
Nield, D. A. and Kuznetsov, A. V. The onset of double-diffusive convection in a nanofluid layer. International Journal of Heat and Fluid Flow, 32, 771–776 (2011)
Gupta, U., Sharma, J., and Wanchoo, R. K. Thermosolutal convection in a horizontal nanofluid layer: introduction of oscillatory motions. Recent Advances in Engineering and Computation Sciences, IEEE, Chandigarh, India (2014)
Yadav, D., Agrawal, G. S., and Bhargava, R. The onset of convection in a binary nanofluid saturated porous layer. International Journal of Theoretical and Applied Multiscale Mechanics, 2, 198–224 (2012)
Gupta, U., Ahuja, J., and Wanchoo, R. K. Magneto convection in a nanofluid layer. International Journal of Heat and Mass Transfer, 64, 1163–1171 (2013)
Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability, Dover Publications, New York (1981)
Kuznetsov, A. V. Non-oscillatory and oscillatory nanofluid bio-thermal convection in a horizontal layer of finite depth. European Journal of Mechanics, B/Fluids, 30, 156–165 (2011)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gupta, U., Sharma, J. & Sharma, V. Instability of binary nanofluids with magnetic field. Appl. Math. Mech.-Engl. Ed. 36, 693–706 (2015). https://doi.org/10.1007/s10483-015-1941-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-015-1941-6