Skip to main content
SpringerLink
Log in

Moment Lyapunov exponent for three-dimensional system under real noise excitation

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

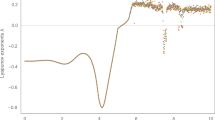
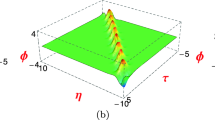
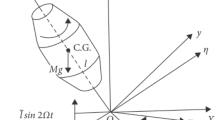
The pth moment Lyapunov exponent of a two-codimension bifurcation system excited parametrically by a real noise is investigated. By a linear stochastic transformation, the differential operator of the system is obtained. In order to evaluate the asymptotic expansion of the moment Lyapunov exponent, via a perturbation method, a ralevant eigenvalue problem is obtained. The eigenvalue problem is then solved by a Fourier cosine series expansion, and an infinite matrix is thus obtained, whose leading eigenvalue is the second-order of the asymptotic expansion of the moment Lyapunov exponent. Finally, the convergence of procedure is numerically illustrated, and the effects of the system and the noise parameters on the moment Lyapunov exponent are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Molcanov, S. A. The structure of eigenfunctions of one-dimensional unordered structures. Math. USSR, Izv., 12(1), 69–101 (1978)

    Article  Google Scholar 

  2. Arnold, L. A formula connecting sample and moment stability of linear stochastic systems. SIAM Journal of Applied Mathematics, 44(2), 793–802 (1984)

    Article  MATH  Google Scholar 

  3. Arnold, L., Kliemann, W., and Oejeklaus, E. Lyapunov exponents of linear stochastic systems. Lyapunov Exponents, Lecture Notes in Mathematics 1186, Springer-Verlag, Berlin, 85–125 (1986)

    Google Scholar 

  4. Arnold, L. and Oejeklaus, E. Almost sure and moment stability for linear equations. Lyapunov Exponents, Lecture Notes in Mathematics 1186, Springer-Verlag, Berlin, 129–159 (1986)

    Google Scholar 

  5. Arnold, L., Doyle, M., and Namachchivaya, S. N. Small noise expansion of moment Lyapunov exponents for two-dimensional systems. Dynamics and Stability of Systems, 12(3), 187–211 (1986)

    Article  Google Scholar 

  6. Namachchivaya, S. N., van Roessel, H., and Doyle, M. Moment Lyapunov exponent for two coupled oscillators driven by real noise. SIAM Journal of Applied Mathematics, 56(3), 1400–1423 (1996)

    Article  MATH  Google Scholar 

  7. Khasminskii, R. and Moshchuk, N. Moment Lyapunov exponent and stability index for linear conservative system with small random perturbation. SIAM Journal of Applied Mathematics, 58(1), 245–256 (1988)

    MathSciNet  Google Scholar 

  8. Namachchivaya, S. N. Moment Lyapunov exponent and stochastic stability of two coupled oscillators driven by real noise. Journal of Applied Mechanics, 68(2), 903–914 (2001)

    Article  MATH  Google Scholar 

  9. Xie, W. C. Moment Lyapunov exponents of a two dimensional system under real noise excitation. Journal of Sound and Vibration, 239(1), 139–155 (2001)

    Article  Google Scholar 

  10. Xie, W. C. Moment Lyapunov exponents of a two dimensional system under bounded noise parametric excitation. Journal of Sound and Vibration, 263(3), 593–616 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  11. Liu, X. B. and Liew, K. M. On the stability properties of a van der Pol-Duffing oscillator that is driven by a real noise. Journal of Sound and Vibration, 285(1–2), 27–49 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  12. Higham, D., Mao, X., and Yuan, C. Almost sure and moment exponential stability in the numerical simulation of stochastic differential equations. SIAM Journal on Numerical Analysis, 45(2), 592–609 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kozic, P., Janevski, G., and Pavlovic, R. Moment Lyapunov exponent and stochastic stability of a double-beam system under compressive axial loading. International Journal of Solids and Structures, 47(10), 1435–1442 (2010)

    Article  MATH  Google Scholar 

  14. Li, S. H. and Liu, X. B. Moment Lyapunov exponent for a three dimensional stochastic system. IUTAM Symposium on Nonliear Stochastic Dynamics and Control, 29(2), 191–200 (2011)

    Article  Google Scholar 

  15. Hu, D. L., Huang, Y., and Liu, X. B. Moment Lyapunov exponent and stochastic stability of binary airfoil driven by non-Gaussian colored noise. Nonlinear Dynamics, 70(3), 1847–1859 (2012)

    Article  MathSciNet  Google Scholar 

  16. Liew, K. M. and Liu, X. B. The maximal Lyapunov exponent for a three-dimensional stochastic system. Journal of Applied Mechanics, 71(2), 677–690 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  17. Guckenheimer, G. and Holmes, P. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Field, Springer-Verlag, New York (1983)

    Google Scholar 

  18. Wedig, W. Lyapunov exponent of stochastic systems and related bifurcation problems. Stochastic Structural Dynamics—Progress in Theory and Applications, Elsevier Applied Science, New York, 315–327 (1988)

    Google Scholar 

  19. Bolotin, V. V. The Dynamic Stability of Elastic Systems, Holden-Day, San Francisco (1964)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Mechanics and Control for Mechanical Structures, College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210014, P. R. China

    Sheng-hong Li  (李胜宏) & Xian-bin Liu  (刘先斌)

  2. School of Mathematics and Physics, Jiangsu University of Science and Technology, Zhenjiang, 212003, Jiangsu Province, P. R. China

    Sheng-hong Li  (李胜宏)

Authors
  1. Sheng-hong Li  (李胜宏)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xian-bin Liu  (刘先斌)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xian-bin Liu  (刘先斌).

Additional information

Project supported by the National Natural Science Foundation of China (Nos. 11072107, 91016022, and 11232007)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, Sh., Liu, Xb. Moment Lyapunov exponent for three-dimensional system under real noise excitation. Appl. Math. Mech.-Engl. Ed. 34, 613–626 (2013). https://doi.org/10.1007/s10483-013-1695-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-013-1695-8

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation