Skip to main content
SpringerLink
Log in

Two-dimensional analyses of delamination buckling of symmetrically cross-ply rectangular laminates

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

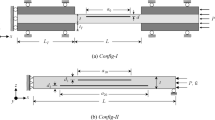
The conventional approach to analysis the buckling of rectangular laminates containing an embedded delamination subjected to the in-plane loading is to simplify the laminate as a beam-plate from which the predicted buckling load decreases as the length of the laminate increases. Two-dimensional analyses are employed in this paper by extending the one-dimensional model to take into consideration of the influence of the delamination width on the buckling performance of the laminates. The laminate is simply supported containing a through width delamination. A new parameter β defined as the ratio of delamination length to delamination width is introduced with an emphasis on the influence of the delamination size. It is found that (i) when the ratio β is greater than one snap-through buckling prevails, the buckling load is determined by the delamination size and depth only; (ii) as the ratio β continues to increase, the buckling load will approach to a constant value. Solutions are verified with the well established results and are found in good agreement with the latter.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Chai, H., Babcock, C. D., and Knauss, W. G. One dimensional modelling of failure in laminated plates by delamination buckling. International Journal of Solids and Structures, 17(11), 1069–1083 (1981)

    Article  MATH  Google Scholar 

  2. Simitses, G. J., Sallam, S., and Yin, W. L. Effect of delamination of axially loaded homogeneous laminated plates. AIAA Journal, 23(9), 1437–1444 (1985)

    Article  Google Scholar 

  3. Yazdi, A. A. and Rezaeepazhand, J. Structural similitude for flutter of delaminated composite beam-plates. Composite Structures, 93, 1918–1922 (2011)

    Article  Google Scholar 

  4. Gu, H. and Chattopadhyay, A. An experimental investigation of delamination buckling and postbuckling of composite laminates. Composites Science and Technology, 59, 903–910 (1999)

    Article  Google Scholar 

  5. Nilsson, K. F., Thesken, J. C., Sindelar, P., Giannqkopoulos, A. E., and Stoåkers, B. A theoretical and experimental investigation of buckling induced delamination growth. Journal of the Mechanics and Physics of Solids, 41(4), 783–807 (1993)

    Article  MathSciNet  Google Scholar 

  6. Parlapalli, M. and Shu, D. Buckling analysis of two-layer beams with an asymmetric delamination. Engineering Structures, 26, 651–658 (2004)

    Article  Google Scholar 

  7. Karihaloo, B. L. and Stang, H. Buckling-driven delamination growth in composite laminates: guidelines for assessing the threat posed by interlaminar matrix delamination. Composites: Part B Engineering, 39, 386–395 (2008)

    Article  Google Scholar 

  8. Gilate, R., Williams, T. O., and Aboudi, J. Buckling of composite plates by global-local plate theory. Composites: Part B Engineering, 32, 229–236 (2001)

    Article  Google Scholar 

  9. Bruno, D. and Greco, F. Mixed mode delamination in plates: a refined approach. International Journal of Solids and Structures, 38(50–51), 9149–9177 (2001)

    Article  MATH  Google Scholar 

  10. Barbero, E. J. and Reddy, J. N. Modeling of delamination in composite laminates using a layerwise plate theory. International Journal of Solids and Structures, 28(3), 373–388 (1991)

    Article  MATH  Google Scholar 

  11. Robbins, D. H., Reddy, J. N., and Krishna, M. A. V. On the modeling of delamination in thick composites. Enhancing Analysis Techniques for Composite Materials, 10, 133–214 (1991)

    Google Scholar 

  12. Lee, J., Gurdal, Z., and Griffin, O. J. Layer-wise approach for the bifurcation problem in laminated composites with delaminations. AIAA Journal, 31(2), 331–338 (1993)

    Article  MATH  Google Scholar 

  13. Tafreshi, A. and Oswald, T. Global buckling behaviour and local damage propagation in composite plates with embedded delaminations. International Journal of Pressure Vessels and Piping, 80, 9–20 (2003)

    Article  Google Scholar 

  14. Qing, G. H., Liu, Y. H., and Li, D. H. A semi-analytical model for the energy release rate analyses of composite laminates with a delamination. Finite Elements in Analysis and Design, 47, 1017–1024 (2011)

    Article  Google Scholar 

  15. Riccio, A., Scaramuzzino, F., and Perugini, P. Embedded delamination growth in composite panels under compressive load. Composites: Part B Engineering, 32(3), 209–218 (2001)

    Article  Google Scholar 

  16. Aslan, Z. and Sahin, M. Buckling behavior and compressive failure of composite laminates containing multiple large delaminations. Composite Structures, 89, 382–390 (2009)

    Article  Google Scholar 

  17. Kyoung, W. M., Kim, C. G., and Hong, C. S. Buckling and post buckling behavior of composite cross-ply laminates with multiple delaminations. Composite Structures, 43, 257–274 (1999)

    Article  Google Scholar 

  18. Lonetti, P. and Zinno, P. Simulation of multiple delaminations in composite laminates under mixed-mode deformations. Simulation Modelling Practice and Theory, 11, 483–500 (2003)

    Article  Google Scholar 

  19. Park, T., Lee, S. Y., and Voyiadjis, G. Z. Finite element vibration analysis of composite skew laminates containing delaminations around quadrilateral cutouts. Composites: Part B Engineering, 40, 225–236 (2009)

    Article  Google Scholar 

  20. Hu, N., Sekine, H., Fukunaga, H., and Yao, Z. H. Impact analysis of composite laminates with multiple delaminations. International Journal of Impact Engineering, 22, 633–648 (1999)

    Article  Google Scholar 

  21. Wang, X. W., Pont-Lezica, I., Harris, J. M., Guild, F. J., and Pavier, M. J. Compressive failure of composite laminates containing multiple delaminations. Composites Science and Technology, 65, 191–200 (2005)

    Article  Google Scholar 

  22. Suemasu, H., Sasaki, W., Ishikawa, T., and Aoki, Y. A numerical study on compressive behavior of composite plates with multiple circular delaminations considering delamination propagation. Composites Science and Technology, 68, 2562–2567 (2005)

    Article  Google Scholar 

  23. Roy, T. and Chakraborty, D. Delamination in FRP laminates with holes under transverse impact. Materials and Design, 29, 124–132 (2008)

    Article  Google Scholar 

  24. Jones, R. M. Mechanics of Composite Materials, 2nd ed., Philadelphia, USA (1980)

    Google Scholar 

  25. Hu, H. T. and Lin, B. H. Buckling optimization of symmetrically laminated plates with various geometries and end conditions. Composites Science and Technology, 55, 277–285 (1995)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanics and Civil Engineering, Jinan University, Guangzhou, 510632, P. R. China

    Jiang-hong Xue  (薛江红), Qing-zi Luo  (罗庆姿) & Ren-huai Liu  (刘人怀)

  2. Key Lab of Disaster Forecast and Control in Engineering, Ministry of Education, Guangzhou, 510632, P. R. China

    Jiang-hong Xue  (薛江红), Qing-zi Luo  (罗庆姿) & Ren-huai Liu  (刘人怀)

  3. State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing, 100081, P. R. China

    Feng Han  (韩峰)

Authors
  1. Jiang-hong Xue  (薛江红)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qing-zi Luo  (罗庆姿)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Feng Han  (韩峰)
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ren-huai Liu  (刘人怀)
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Project supported by the National Natural Science Foundation of China (Nos. 11172113, 11032005, and 11072037)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xue, Jh., Luo, Qz., Han, F. et al. Two-dimensional analyses of delamination buckling of symmetrically cross-ply rectangular laminates. Appl. Math. Mech.-Engl. Ed. 34, 597–612 (2013). https://doi.org/10.1007/s10483-013-1694-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-013-1694-7

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation