Skip to main content
SpringerLink
Log in

Solitary wave solution to Aw-Rascle viscous model of traffic flow

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

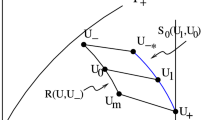
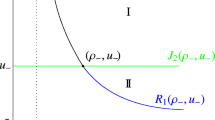
A traveling wave solution to the Aw-Rascle traffic flow model that includes the relaxation and diffusion terms is investigated. The model can be approximated by the well-known Kortweg-de Vries (KdV) equation. A numerical simulation is conducted by the first-order accurate Lax-Friedrichs scheme, which is known for its ability to capture the entropy solution to hyperbolic conservation laws. Periodic boundary conditions are applied to simulate a lengthy propagation, where the profile of the derived KdV solution is taken as the initial condition to observe the change of the profile. The simulation shows good agreement between the approximated KdV solution and the numerical solution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Lighthill, M. J. and Whitham, G. B. On kinematic waves: II. a theory of traffic flow on long crowded roads. Proceedings of the Royal Society of London, Series A, 229(1178), 317–345 (1955)

    Article  MathSciNet  MATH  Google Scholar 

  2. Richards, P. I. Shockwaves on the highway. Operations Research, 4(1), 42–51 (1956)

    Article  MathSciNet  Google Scholar 

  3. Kerner, B. S. and Konhäuser, P. Structure and parameters of clusters in traffic flow. Physical Review E, 50, 54–83 (1994)

    Article  Google Scholar 

  4. Kühne, R. D. Macroscopic freeway model for dense traffic-stop-start waves and incident detection. Proceedings of the 9th International Symposium on Transportation and Traffic Theory (eds. Volmuller, J. and Hamerslag, R.), VNU Science Press, Utrecht, 21–42 (1984)

    Google Scholar 

  5. Payne, H. J. Models of freeway traffic and control. Mathematical Models of Public Systems (ed. Bekey, A. G.), Simulation Council Proc., La Jola, 51–61 (1971)

    Google Scholar 

  6. Whitham, G. B. Linear and Nonlinear Waves, John Wiley and Sons, New York (1974)

    MATH  Google Scholar 

  7. Zhang, P., Wong, S. C., and Dai, S. Q. A conserved higher-order anisotropic traffic flow model: description of equilibrium and non-equilibrium flows. Transportation Research Part B, 43, 562–574 (2009)

    Article  Google Scholar 

  8. Aw, A. and Rascle, M. Resurrection of “second order” models of traffic flow. SIAM Journal on Applied Mathematics, 60, 916–938 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  9. Rascle, M. An improved macroscopic model of traffic flow: derivation and links with the Lighthill-Whitham model. Mathematical and Computer Modelling, 35, 581–590 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  10. Greenberg, J. M. Congestion redux. SIAM Journal on Applied Mathematics, 64, 1175–1185 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  11. Zhang, P., Wu, C. X., and Wong, S. C. A semi-discrete model and its approach to a solution for wide moving jam in traffic flow. Physica A, 391, 456–463 (2012)

    Article  Google Scholar 

  12. Xu, R. Y., Zhang, P., Dai, S. Q., and Wong, S. C. Admissibility of a wide cluster solution in anisotropic higher-order traffic flow models. SIAM Journal on Applied Mathematics, 68, 562–573 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  13. Zhang, P., Wong, S. C., and Dai, S. Q. Characteristic parameters of a wide cluster in a higher-order traffic flow model. Chinese Physics Letters, 232, 516–519 (2006)

    Google Scholar 

  14. Zhang, P. and Wong, S. C. Essence of conservation forms in the traveling wave solutions of higher-order traffic flow models. Physical Review E, 74, 026109 (2006)

    Article  MathSciNet  Google Scholar 

  15. Kerner, B. S., Klenov, S. L., and Konhäuser, P. Asymptotic theory of traffic jams. Physical Review E, 56, 4199–4216 (1997)

    Article  Google Scholar 

  16. Wu, C. X., Zhang, P., Dai, S. Q., and Wong, S. C. Asymptotic solution of a wide cluster in Kühne’s higher-order traffic flow model. Proceedings of the 5th International Conference on Nonlinear Mechanics (ed. Chien, W. Z.), Shanghai University Press, Shanghai, 1132–1136 (2007)

    Google Scholar 

  17. Berg, P. and Woods, A. On-ramp simulation and solitary waves of a car-following model. Physical Review E, 64, 035602 (2001)

    Article  Google Scholar 

  18. Ge, H. X. and Han, X. L. Density viscous continuum traffic flow model. Physica A, 371, 667–673 (2006)

    Article  Google Scholar 

  19. Li, T. Stability of traveling waves in quasi-linear hyperbolic systems with relaxation and diffusion. SIAM Journal on Mathematical Analysis, 40, 1058–1075 (2008)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai, 200072, P. R. China

    Chun-xiu Wu  (吴春秀), Peng Zhang  (张 鹏), Dian-liang Qiao  (乔殿梁) & Shi-qiang Dai  (戴世强)

  2. College of Mathematics and Computer Science, Quanzhou Normal University, Quanzhou, 362000, Fujian Province, P. R. China

    Chun-xiu Wu  (吴春秀)

  3. Department of Civil Engineering, The University of Hong Kong, Hong Kong, P. R. China

    S. C. Wong

Authors
  1. Chun-xiu Wu  (吴春秀)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Peng Zhang  (张 鹏)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. C. Wong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Dian-liang Qiao  (乔殿梁)
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shi-qiang Dai  (戴世强)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Peng Zhang  (张 鹏).

Additional information

Project supported by the National Natural Science Foundation of China (Nos. 11072141 and 11272199), the National Basic Research Program of China (No. 2012CB725404), and the University Research Committee, HKU SPACE Research Fund and Faculty of Engineering Top-up Grant of the University of Hong Kong (No. 201007176059)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wu, Cx., Zhang, P., Wong, S.C. et al. Solitary wave solution to Aw-Rascle viscous model of traffic flow. Appl. Math. Mech.-Engl. Ed. 34, 523–528 (2013). https://doi.org/10.1007/s10483-013-1687-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-013-1687-9

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation