Abstract
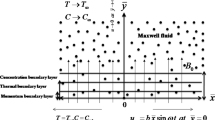
Two fundamental flows, namely, the Stokes and Couette flows in a Maxwell fluid are considered. The exact analytic solutions are derived in the presence of the slip condition. The Laplace transform method is employed for the development of such solutions. Limiting cases of no-slip and viscous fluids can be easily recovered from the present analysis. The behaviors of embedded flow parameters are discussed through graphs.
Similar content being viewed by others
References
Fetecau, C., Athar, M., and Fetecau, C. Unsteady flow of a generalized Maxwell fluid with fractional derivative due to a constantly accelerating plate. Computers and Mathematics with Applications, 57, 596–603 (2009)
Vieru, D. and Fetecau, C. Flow of a viscoelastic fluid with the fractional Maxwell model between two side walls perpendicular to a plate. Applied Mathematics and Computation, 200, 459–464 (2008)
Vieru, D., Akhtar, W., and Fetecau, C. Starting solutions for the oscillating motion of a Maxwell fluid in cylindrical domains. Meccanica, 42, 573–583 (2008)
Fetecau, C. and Fetecau, C. A new exact solution for the flow of a Maxwell fluid past an infinite plate. International Journal of Non-Linear Mechanics, 38, 423–427 (2007)
Ali, N., Hayat, T., and Asghar, S. Peristaltic flow of a Maxwell fluid in a channel with compliant walls. Chaos, Solitons & Fractals, 39, 407–416 (2009)
Hayat, T. and Abbas, Z. Channel flow of a Maxwell fluid with chemical reaction. Z. Angew. Math. Phys., 9, 124–144 (2008)
Hayat, T., Abbas, Z., and Sajid, M. Series solution for the upper-convected Maxwell fluid over a porous stretching plate. Physics Letters A, 358, 396–403 (2006)
Abbas, Z., Sajid, M., and Hayat, T. MHD boundary-layer flow of an upper-convected Maxwell fluid in a porous channel. Theoretical and Computational Fluid Dynamics, 20, 229–238 (2006)
Hayat, T., Nadeem, S., and Asghar, S. Periodic unidirectional flows of a viscoelastic fluid with the fractional Maxwell model. Applied Mathematics and Computation, 151, 153–161 (2004)
Jamil, M. and Fetecau, C. Helical flows of Maxwell fluid between coaxial cylinders with given shear stresses on the boundary. Nonlinear Analysis: Real World Applications, 11, 4302–4311 (2010)
Tan, W. C., Peng, W. X., and Xu, M. Y. A note on unsteady flows of a viscoelastic fluid with the fractional Maxwell model between two parallel plates. International Journal of Non-Linear Mechanics, 38, 645–650 (2003)
Tan, W. C. and Xu, M. Y. Plane surface suddenly set in motion in a viscoelastic fluid with fractional Maxwell model. Acta Mechanica Sinica, 18, 342–349 (2002)
Wang, S. W. and Tan, W. C. Stability analysis of double-diffusive convection of Maxwell fluid in a porous medium heated from below. Physics Letters A, 372, 3046–3050 (2008)
Wang, Y. and Hayat, T. Fluctuating flow of a Maxwell fluid past a porous plate with variable suction. Nonlinear Analysis: Real World Applications, 9, 1269–1282 (2008)
Rao, I. J. and Rajagopal, K. R. On a new interpretation of the classical Maxwell model. Mechanics Research Communications, 34, 509–514 (2007)
Jia, J. H., Shen, X. Y., and Hua, H. X. Viscoelastic behavior analysis and application of the fractional derivative Maxwell model. Journal of Vibration and Control, 13, 385–401 (2007)
Khaled, A. R. A. and Vafai, K. The effect of the slip condition on Stokes and Couette flows due to an oscillating wall: exact solutions. International Journal of Non-Linear Mechanics, 39, 795–809 (2004)
Erdogan, M. E. A note on an unsteady flow of a viscous fluid due to an oscillating plane wall. International Journal of Non-Linear Mechanics, 35, 1–6 (2000)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hayat, T., Zaib, S., Asghar, S. et al. Transient flows of Maxwell fluid with slip conditions. Appl. Math. Mech.-Engl. Ed. 34, 153–166 (2013). https://doi.org/10.1007/s10483-013-1660-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-013-1660-8